Основные понятия и определения теории множеств.
Понятие множества. Дискретные множества. Способы задания.
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами.
Пример. Множества натуральных чисел N, целых Z, действительных R.
Если объект а является элементом множества А, то говорят, что а принадлежит А. Обозначение: а 
А. В противном случае а 
А.
Пример. а = 4 является элементом множества А ={2;3;4;5}, т.е. а А.
Пример. b = 8 не является элементом множества А ={2;3;4;5}, т.е. b А.
Множества могут быть конечными(дискретными) и бесконечными. Множество, не содержащее элементов, называют пустым. Обозначение Ø.
Множество может быть задано различными способами:
перечислением элементов: А ={ а1, а2 ,…, аn };
характеристическим предикатом (условием): А ={ x | Р(х)};
порождающей процедурой: А ={ x | х=f }.
Пример. M ={1,2,3,4,5}. Данное множество может быть записано следующим образом: M ={ x | х N и х < 6 }.
Перечислением можно задавать только конечные множества. Бесконечные множества задаются только характеристическим предикатом или порождающей процедурой.
Если каждый элемент множества А является элементом множества B, то говорят, что множество А является подмножеством множества B. Обозначение:
А 
B 
х А 
х B.
Два множества равны, если они являются подмножествами друг друга:
А = B А B и B А.
Можно показать, что А B и B С А С.
Если А B и А≠B, то множество А называется собственным подмножеством множества B.
Замечание. Если требуется различать собственные и несобственные подмножества, то для обозначения собственных подмножеств используют знак , а для несобственных – знак 
.
Пример. А B и B С А С.
Говорят, что между множествами А и B установлено взаимно однозначное соответствие, если каждому элементу множества А соответствует один и только один элемент множества B и каждому элементу множества B соответствует некоторый элемент множества А. В этом случае говорят также, что множества А и B изоморфны и используют обозначение: А ~ B.
Отметим некоторые свойства взаимно однозначного соответствия множеств:
1. А ~ А.
2. А ~ B B ~ А.
3. А ~ B и B ~ С А ~ С.
Если между двумя множествами А и B может быть установлено взаимно однозначное соответствие, то говорят, что множества имеют одинаковую мощность или равномощны, и записывают: | А |= | B |.
Пример. Множество различных месяцев в году равномощно множеству знаков зодиака и множеству А ={2; 4; 5; 7; 11; 15; 25; 37; 56; 100; 111; 333}, содержащему 12 различных элементов.
Пример. Множество натуральных чисел имеет мощность |N|= 
.
Теорема. Множество, имеющее бесконечное подмножество, бесконечно:
А B и | А |= | B |= .
Следствие. Все подмножества конечного множества конечны.
Парадокс Рассела
Парадокс Рассела демонстрирует несовершенство и недостаточность интуитивных представлений о множествах. Прежде чем привести формулировку парадокса Рассела, остановимся на трех важных моментах.
Существуют множества, которые содержат другие множества в качестве своих элементов, например, множество целых чисел содержит множество натуральных чисел.
Существуют множества, которые не являются элементами самих себя.
Если какое-то множество определено корректно, то всегда (имеется в виду - для любого объекта) должен существовать однозначный ответ на вопрос, принадлежит ли выбранный объект данному множеству.
Теперь рассмотрим множество F, содержащее те и только те множества, которые не являются элементами самих себя.
Парадокс состоит в том, что после такого способа задания множества F мы не можем однозначно ответить на вопрос: само множество F как элемент принадлежит F или нет?
"Житейским" или ситуационным аналогом парадокса Рассела является известный рассказ о брадобрее.
Брадобрей воинской части получает приказ от командира брить всех тех, кто не бреется сам, но при этом, в целях экономии времени, ему запрещено брить всех тех, кто бреется самостоятельно. Теперь зададим вопрос: может ли брадобрей побрить самого себя?
Если ответ - "да", то он принадлежит к тем, кто бреется самостоятельно, но таких ему брить запрещено. Если - "нет", то он принадлежит к тем, кто сам не бреется, а такого человека он брить обязан.
Операции над множествами
Рассмотрим основные операции над множествами:
объединение: А 
B = { x | х А или х B };
пересечение: А 
B = { x | х А и х B };
разность: А \ B = { x | х А и х 
B };
симметрическая разность: А 
B = (А B)\ (А B) =
={ x | (х А и х B) или (х B и х А)};
дополнение: 
={ x | х А }.
Операция дополнения подразумевает, что задан некоторый универсум U, и = U \ А. В противном случае операция дополнения не определена.
Пример. Пусть А ={2; 4; 5}, B ={3; 4; 5}. Тогда
А B = { 2; 3; 4; 5}; А 
B = {4; 5}; А \ B = {2}; А B ={2; 3}.
Основные тождества алгебры множеств
Для произвольных множеств А, В, и С справедливы следующие соотношения:
Коммутативность:
A Ç 
= Ç A,
A È = È A,
Идемпотентность:
К Ç A = A,
A È A = A,
Закон двойного отрицания: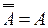 
,
Законы действия с пустым и универсальным множествами
,
,
Æ,
Æ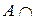=Æ,
Æ= A,
U 
= U.
Законы де Моргана: 
, 
,
Дистрибутивность пересечения относительно объединения:
,
Дистрибутивность объединения относительно пересечения:
,
Законы склеивания (A Ç )È(A Ç 
)= A, (A È )Ç(A È )= A,
Законы поглощения A È(A Ç )= A, A Ç (A Ç )= A,
Разность множеств: 
.
Пример. Докажите тождество 
= 
.
Решение
=
= 
=
= 
=
= 
=
= 
=
= 
= .
При преобразовании были использованы следующие формулы:
,
,
,
,
,
,
,
.
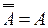На рисунке приведены диаграммы Венна (называемые часто также кругами Эйлера), иллюстрирующие операции над множествами. Сами исходные множества изображены овалами, а результат выделен штриховкой.
Пример.
20 человек знают английский и 10 - немецкий, из них 5 знают и английский, и немецкий. Сколько человек всего?
Решение:
10+20-5=25.
Ответ: 25 человек.
Пример.
Из 100 студентов потока переживают за оценку на экзамене по высшей математике 30 человек, по дискретной математике - 28, по истории - 42. Дискретную и высшую математику одновременно боятся сдавать 8 человек, дискретную математику и историю - 10, высшую математику и историю - 5, все три предмета – 3 студента. Сколько студентов не переживают за сдачу ни одного из этих предметов?
Решение:
Выразим условие этой задачи графически. Обозначим кругом тех, кто боится сдавать высшую математику, другим кругом - тех, кто переживает за дискретную математику, и третьим кругом - тех, кто опасается за оценку по истории.
Все три предмета бояться сдавать 3 студента, значит, в общей части кругов вписываем число 3. Дискретную и высшую математику одновременно боятся сдавать 8 человек, а 3 из них владеют еще и историю. Следовательно, только дискретную и высшую математику боятся 8-3=5 человек.
Аналогично получаем, что только дискретную математику и историю боятся 10-3=7 человек, а высшую математику и историю 5-3=2 студента. Вносим эти данные в соответствующие части.
Определим теперь, сколько студентов переживают только за один предмет. Экзамен по высшей математике боятся 30 человек, но 5+3+2=10 из них переживают ещё и за другие предметы, следовательно, только высшую математику бояться 20 человек. Аналогично получаем, что одну дискретную математику боятся 13 студентов, а одну историю - 30 человек.
По условию задачи всего 100 студентов. 20+13+30+5+7+2+3=80 студентов боятся сдавать хотя бы один предмет, следовательно, 20 человек не переживают ни за одним из этих экзаменов.
Ответ: 20 студентов не переживают за сдачу экзамена ни по одному из этих предметов.
Мощность множеств
Мощность множества,— это характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
В основе этого понятия лежат естественные представления о сравнении множеств:
1. Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), называются равномощными. Для конечных множеств это означает, что они содержат одинаковое количество элементов (имеют одинаковую мощность).
2. Обратно: множества, равные по мощности, должны допускать такое взаимно-однозначное соответствие.
3. Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).
Т.е. для множеств с конечным числом элементов мощность равна числу элементов множества.
Для бесконечных множеств даже взаимно-однозначное соответствие не означает «равенства» в обычном представлении. Например, y=2x, заданная при xÎ[0,1] дает взаимно-однозначное соответствие с множеством yÎ[0,2].
До построения теории мощности множеств, множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.
Мощность множеств позволяет сравнивать бесконечные множества.
Число элементов конечного множества называется мощностью множества и обозначается символом |A|.
Булеан.
Множество всех подмножеств данного множества называют булеаном множества. Булеан обозначают символом B(A).
Пример 1.5. Пусть A = { 1,2,3 }. Перечислить элементы булеана множества A.
B(A)={ Æ,{ 1 },{ 2 },{ 3},{ 1,2 },{ 1,3 },{ 2,3},{ 1,2,3 } }.
Пусть множество А конечно и состоит из n элементов, т.е. |A| = n. Тогда мощность множества |B(A) | =2n. Это можно доказать методом математической индукции.