Сложение вероятностей иамплитуд

Если какое-то событие может произойти двумя различными способа- ми, и мы знаем вероятность каждого из этих способов, то классическая вероятность события вычисляется как сумма вероятностей этих способов.

Если из начального состояния 1 классическая система попадает в ко- нечное состояние 3 через промежуточное состояние 2 или 2j, то мы можем записать:

p(1→2→3 или 1→2r→3) = p(1→2→3)+p(1→2r→3). (3.2)

Если конечный результат чуть-чуть различается и классическая система в одном случае в итоге попадает в состояние 3, а в другом в чуть-чуть отличное состояние 3j, то вероятности по-прежнемускладываются:

p(1→2→3 или 1→2r→3r) = p(1→2→3)+p(1→2r→3r). (3.3)

Таким образом, в классике мы можем не различать похожие результаты 3 и 3j и произвольным образом огрублять конечный результат, т. к. на вы- числении вероятностей это нескажется.

В квантовой механике формулу (3.2), для случая когда конечный ре- зультат в точности совпадает, необходимо заменить аналогичной фор- мулой для амплитуд

A(1→2→3 или 1→2r→3) = A(1→2→3) +A(1→2r→3), (3.4)

а формулу (3.3), для случая когда конечный результат хотя бы чуть-чуть отличается, следует оставить без изменений.

 

 

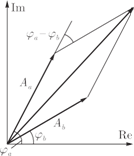
Рис. 3.2. Сложение амплитуд вероятности.

 

Возводя формулу (3.4) в квадрат, получаем (для упрощения записи здесь (1 → 2 → 3) обозначается как a, а (1 → 2j → 3) — как b)

p(a или b) = |A(a или b)|2 =

=|A_a|2+|A_b|2+(A^∗aA_b+A_aA^∗b)=

=|A_a|2 +|A_b|2+2|A_a||A_b|cos(ϕ_a−ϕ_b)= (3.5)

= p_a+ p_b+ 2√p_ap_bcos(ϕ_a− ϕ_b).

Здесь ϕ_a= arg A_a, ϕ_b= arg A_b— фазы амплитуд вероятности. В третьей строчке формулы мы воспользовались теоремой косинусов.

Формула (3.5) отличается от (3.2) лишним членом, который называет- ся интерференционным членом:

(A^∗aA_b+A_aA^∗b)=2|A_a||A_b|cos(ϕ_a−ϕ_b)=2√p_ap_bcos(ϕ_a−ϕ_b).(3.6)

| |

| | −

| | | |

Интерференционный член, как правило, не является малой поправкой, он сравним по величине с классическими слагаемыми. В зависимости от раз- ности фаз между амплитудами интерференционный член может быть по- ложительным,отрицательнымилинуле¨м.Так,еслиA_a=A_b,токван- товая вероятность p_(aилиb)= 2 A_a²(1 + cos(ϕ_a ϕ_b)) может меняться от нуля до удвоенной классической вероятности 4 A_a².

Почему мы не видим интерференционного члена в классических опы- тах? Это может происходить по одной из двух причин.

1. В классических опытах мы не можем зафиксировать фазы амплитуд вероятности, которые случайно меняются от опыта к опыту. В результа- тепроисходитусреднениепофазе,иинтерференционныйчленисчезает.

 

Если мы плохо различаем похожие, но не совпадающие состояния систе- мы (как в классике), то мы вместо реальной интерференционной картины наблюдаемусредне¨нную(сглаженную),апосколькуинтерференционный член оказывается быстро осциллирующим, при усреднении по нескольким похожим результатам он можетисчезнуть.

2. Другаяпричинаисчезновенияинтерференционногочлена—наблю- дение (неконтролируемое взаимодействие системы с окружением, возмож- но непроизвольное), которое в принципе позволяет определить как именно система прошла из начального состояния в конечное. Таким образом,попа- дание системы в одну точку разными путями будет различимым, поскольку информация о пути либо известна, либо «записана» в окружении. А для различимых событий мы должны складывать не амплитуды, а вероятности, т. е. интерференционный членисчезает.