ПРАКТИКУМ 3.1–РАСЧЕТ МОДЕЛЬ ОЦЕНКИ КАПИТАЛЬНЫХ АКТИВОВ CAPM (АЛЬТЕРНАТИВНО ЛЕКЦИИ)
Бета-коэффициент. 1
Бета-коэффициент портфеля. 3
Бета-коэффициент
В портфельной теории бета-коэффициент (англ. Beta, β) является показателем, который характеризует риск, привносимый в рыночный портфель отдельной акцией. Чтобы рассчитать его значение необходимо воспользоваться следующей формулой:
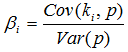
где Cov (ki, p) – ковариация доходности i-ой ценной бумаги (ki) и доходности портфеля (p).
Var (p) – вариация доходности портфеля (p).
В расширенном виде формулу для расчета бета-коэффициента можно записать следующим образом:
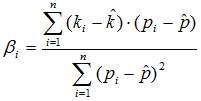
где ki – доходность ценной бумаги в i-ом периоде;
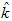- ожидаемая (средняя) доходность ценной бумаги;
pi – доходность портфеля в i-ом периоде;
- ожидаемая (средняя) доходность портфеля.
n – количество наблюдений.
Интерпретация бета-коэффициента
β < 0 – доходность акции демонстрирует разнонаправленное движение с доходностью портфеля или индекса рынка, интерпретация осуществляется по абсолютному значению.
β = 0 – отсутствует корреляция между доходностью акции и доходностью портфеля или индекса рынка.
0 < β < 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное движение, однако волатильность доходности акций ниже, чем волатильность доходности портфеля.
β = 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное движение, при этом волатильность доходности акции равна волатильности доходности портфеля.
β > 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное движение, при этом волатильность доходности акции выше волатильности доходности портфеля.
Пример расчета
Динамика доходности акций Компании А и Компании Б, а также динамика доходности портфеля представлены в таблице:
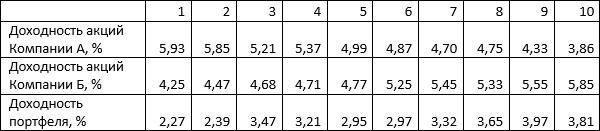
Ожидаемая доходность акций Компании А составит 4,986%, Компании Б 5,031% и портфеля 3,201%.
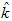А= (5,93+5,85+5,21+5,37+4,99+4,87+4,70+4,75+4,33+3,86)/10 = 4,986%
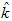Б= (4,25+4,47+4,68+4,71+4,77+5,25+5,45+5,33+5,55+5,85)/10 = 5,031%
= (2,27+2,39+3,47+3,21+2,95+2,97+3,32+3,65+3,97+3,81)/10 = 3,201%
Подставим полученные данные в приведенную выше формулу расчета бета-коэффициента.
βА = ((5,93-4,986)(2,27-3,201) + (5,85-4,986)(2,39-3,201) + (5,21-4,986)(3,47-3,201) + (5,37-4,986)(3,21-3,201) + (4,99-4,986)(2,95-3,201) + (4,87-4,986)(2,97-3,201) + (4,70-4,986)(3,32-3,201) + (4,75-4,986)(3,65-3,201) + (4,33-4,986)(3,97-3,201) + (3,86-4,986)(3,81-3,201)) / ((2,27-3,201)2+ (2,39-3,201)2+ (3,47-3,201)2+ (3,21-3,201)2+ (2,95-3,201)2+ (2,97-3,201)2+ (3,32-3,201)2+ (3,65-3,201)2+ (3,97-3,201)2+ (3,81-3,201)2) = -0,975
βБ = ((4,25-5,031)(2,27-3,201) + (4,47-5,031)(2,39-3,201) + (4,68-5,031)(3,47-3,201) + (4,71-5,031)(3,21-3,201) + (4,77-5,031)(2,95-3,201) + (5,25-5,031)(2,97-3,201) + (5,45-5,031)(3,32-3,201) + (5,33-5,031)(3,65-3,201) + (5,55-5,031)(3,97-3,201) + (5,85-5,031)(3,81-3,201)) / ((2,27-3,201)2+ (2,39-3,201)2+ (3,47-3,201)2+ (3,21-3,201)2+ (2,95-3,201)2+ (2,97-3,201)2+ (3,32-3,201)2+ (3,65-3,201)2+ (3,97-3,201)2+ (3,81-3,201)2) = 0,755
Итак, доходность акций Компании А демонстрирует разнонаправленное движение с доходностью рыночного портфеля, о чем свидетельствует отрицательное значение бета-коэффициента -0,975. При этом его абсолютное (по модулю) значение свидетельствует о том, что риск инвестирования в эти ценные бумаги практически равен рыночному (когда β = 1).
Доходность акций Компании Б, напротив, демонстрирует однонаправленное движение с доходностью рыночного портфеля, что подтверждает положительное значение бета-коэффициента. При этом риск инвестирования в эти ценные бумаги также ниже рыночного.
Бета-коэффициент портфеля
Современные концепции инвестирования решают две задачи: снижение диверсифицируемого риска и увеличение ожидаемой доходности. Их решение лежит в плоскости формирования портфеля, который будет включать не одну, а множество ценных бумаг, что позволит диверсифицировать риски. Тем не менее, осуществление инвестиций в такой портфель предполагает определенный уровень риска, мерой которого является бета-коэффициент портфеля. Этот показатель будет напрямую зависеть от уровня риска, присущего инвестированию в каждую из ценных бумаг, входящих в такой портфель.
Формула
Формула расчета бета-коэффициента портфеля учитывает бета-коэффициент каждой из ценных бумаг, а также их удельный вес:
где wi – удельный вес i-ой ценной бумаги в портфеле;
βi- бета-коэффициент i-ой ценной бумаги;
n – количество ценных бумаг в портфеле.
Пример расчета
Инвестор сформировал портфель ценных бумаг из акций трех компаний, историческая доходность которых, а также историческая доходность рыночного портфеля, представлена в таблице.
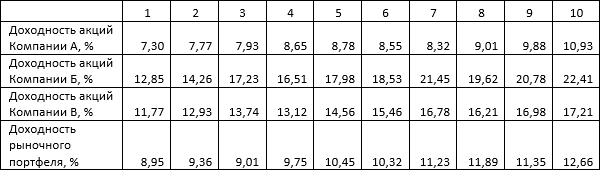
При этом удельный вес акций Компании А в портфеле составляет 40%, акций Компании Б 30% и акций Компании В 30%.
Ожидаемая доходность акций Компании А составит 8,712%, Компании Б 18,162%, Компании В 14,876%, рыночного портфеля 10,497%.
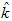А(ожидаемая (средняя) доходность акции)= (7,30+7,77+7,93+8,65+8,78+8,55+8,32+9,01+9,88+10,93)/10 = 8,712%
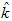Б(ожидаемая (средняя) доходность акции)= (12,85+14,26+17,23+16,51+17,98+18,53+21,45+19,62+20,78+22,41)/10 = 18,162%
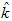В(ожидаемая (средняя) доходность акции)= (11,77+12,93+13,74+13,12+14,56+15,46+16,78+16,21+16,98+17,21)/10 = 14,876%
(ожидаемая (средняя) доходность портфеля)= (8,95+9,36+9,01+9,75+10,45+10,32+11,23+11,89+11,35+12,66)/10 = 10,497%
Ожидаемая доходность портфеля, включающего акции этих трех компаний в указанной пропорции, составит 13,396%.
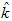p= 0,4*8,712+0,3*18,162+0,3*14,876 = 13,396%
Чтобы рассчитать бета-коэффициент портфеля, необходимо рассчитать бета-коэффициент каждой из акций. Для акций Компании А он составит 0,72, для акций Компании Б 2,16 и для акций Компании В 1,39. (О том, как рассчитать бета-коэффициент акций можно прочитать здесь)
Подставив полученные результаты в приведенную выше формулу рассчитаем бета-коэффициент портфеля, который составит 1,35.
βp= 0,4*0,72+0,3*2,16+0,3*1,39 = 1,35
Интерпретация
Интерпретация значения бета-коэффициента портфеля ценных бумаг такая же, как и для отдельной ценной бумаги.
1. β < 0 – очень редко встречается на практике, свидетельствует о том, что доходность портфеля ценных бумаг демонстрирует разнонаправленное движение с доходностью рыночного портфеля.
2. β = 0 – очень редко встречается на практике, свидетельствует об отсутствии корреляция между доходностью портфеля ценных бумаг и доходностью рыночного портфеля.
3. 0 < β < 1 – доходность портфеля ценных бумаг и рыночного портфеля демонстрируют однонаправленное движение, однако уровень риска первого, ниже чем у второго (бета-коэффициент рыночного портфеля всегда равен 1).
4. β = 1 – риски портфеля ценных бумаг и рыночного портфеля равны, а их доходность демонстрирует однонаправленное движение.
5. β > 1 – риски, связанные с инвестирование в портфель ценных бумаг, выше чем при инвестировании в рыночный портфель, а их доходность демонстрирует однонаправленное движение.