Принцип Даламбера-Лагранжа

Расчетно-пояснительная записка

Разработал студент _________________________________________

Подпись, дата Инициалы, фамилия

Руководитель _________________________________________

Подпись, дата Инициалы, фамилия

Члены комиссии _________________________________________

Подпись, дата Инициалы, фамилия

Нормоконтролер __________________________________________

Подпись, дата Инициалы, фамилия

 

Защищена__________________________Оценка_______________________________

дата

 

ВОРОНЕЖ

Замечания руководителя

 

 

 

Содержание:

 

Условие задачи ……………………………………………………………………… Стр. 4

Кинематический анализ ……………………………………………………… Стр. 6

Расчёт кинетической энергии …………………………………………….. Стр. 8

Расчёт инерции тел системы ……………………………………………… Стр. 10

Принцип Даламбера-Лагранжа …………………………………………. Стр. 12

Уравнение Лагранжа ………………………………………………………….. Стр. 18

 

 

Условие задачи

 

Рис. 1

 

 

Механическая система тел 1-5 (рис. 1) движется под воздействием постоянных сил тяжести, так же присутвует момент .

Найти уравнение движения системы в обобщённых координатах и при заданных начальных условиях. Необходимые данные приведены в табл.1.

При решении задачи массами нитей пренебрегаем, считаем, что качение колёс происходит без проскальзывания, трение качения и силы сопротивления в подшипниках не учитываются.

 

Табл.1

Массы тел	Момент M	Коэффициент Трения скольжения	Обобщённые координаты
1	2	3	4	5	q1	q2
2m	2m	m	m	3m	M	f	x	ξ

^ФЫЫЫЫЫРРР

 

 

Начальные условия:

(1)

(2)

(3)

(4)

 

Кинематический анализ

 

 

Рис. 2

 

Движение №1, №2,№3- поступательное

Движение №4- плоское

Движение №5- вращательное

 

 

 

Выразим скорости через обобщённые координаты:

 

– число степеней свободы

- обобщённая координата

– обобщённая координата

 

V₁ (1.1)

V₂ (1.2)

V₃ (1.3)

V_c (1.4)

W₄ (1.5)

W₅ (1.6)

Примечание:

Радиусы тел выражены согласно (Рис.2)

 

Таблица скоростей

V1	V2	V3	Vc	W4	W5

 

Табл.2

 

 

Расчёт кинетической энергии

Кинетическая энергия в соответствие с (Рис. 2) будет равна сумме энергий всех тел системы

(2.1)

 

Рассчитаем энергию каждого тела отдельно:

Движение тел №1, №2, №3поступательное см. (Рис.2), поэтому кинетическая энергия этих тел будет равна:

(2.2)

(2.3)

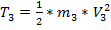(2.4)

Тело №4 имеет плоское движение, в соответствие с этим энергия будет равна:

(2.5)

Где: (2.6) – момент инерции

Тело №5 имеет вращательное движение, поэтому энергия примет вид:

(2.7)

Где: (2.8) – момент инерции

 

Сложим получившиеся выражения в соответствие с формулой (2.1) и заменим скорости тел (Табл.2), так же подставим значения момента инерции:

(2.9)

 

 

Подставим в выражение (2.9) значения масс и запишем выражение в виде:

(2.10)

 

(2.11)

Где:

(2.12)

(2.13)

(2.14)

Подставим значения масс (Табл. 1) в формулу (2.11)

Формула (2.11) примет вид:

(2.12)

Где:

(2.13)

(2.14)

(2.15)

 

Расчёт инерции тел системы

 

Рис.3

 

 

 

Таблица ускорений

 

Табл.3

 

Запишем силы инерции для всех тел:

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)где:

(3.6) где:

Выразим силы инерции через обобщённые координаты и подставим ускорения согласно табл.3

 

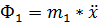(3.7)

(3.8)

(3.9)

(3.10)

(3.11)

(3.12)

 

Принцип Даламбера-Лагранжа

Рис.4

 

 

Таблица виртуальных перемещений

δs1	δs2	δS3	δsc	δɣ4	δɣ5
δx	δ (x+ξ)	δ (x-ξ)	δx	δ	δ

 

Табл.4

 

Найдём работу всех сил действующих на систему

Cилы действующие на систему:

{P₁; F_тр; R_x; R_y; P₅; P_c; P₃; P₂; M}

Силы, совершающие работу:

{P₁; F_тр; P_c; P₃; P₂; M}

Остальные силы совершать работу не будут, так как перемещения этих сил равны нулю.

1) Найдём виртуальную работу сил системы при δx≠0 и δξ=0

δA₁ (4.1)

примечание: сила P₁умножается на cos(60), так как угол между скоростью первого тела и силой действующей на это тело равен 60.

Найдём значение силы трения:

(4.2)

Где:

N (4.3) – сила реакции опоры

Подставив в формулу (4.2) формулу (4.3) изначение массы, согласно табл.1, получим окончательное значение силы трения

(4.4)

Учитывая значения силы трения и виртуальных перемещений (Табл.4), запишем формулу (4.1) в следующем виде:

(4.5)

 

Раскрывая скобки и учитывая, что δξ=0 получим:

(4.6)

Где:

Q₁ (4.7)

(4.8)

Подставив в формулу (4.7) формулу (4.8), учитывая значения масс (табл.1) соответственно, получим формулу для Q₁в общем виде

(4.9)

2) Найдём виртуальную работу при условии δx=0 и δξ≠0

(4.10)

Учитывая, что δx=0, получим:

(4.11)

Где:Q₂ 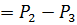(4.12)

Учитывая формулу (4.8) и (табл.1) получим значение Q₂в общем виде

(4.13)

 

 

 

Найдём работу сил инерции действующих на систему

1) Найдём работу сил инерции, учитывая, что δX≠0 и δξ=0

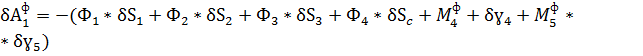(4.14)

Подставим в формулу (4.14) группу формул 3.7-12 соответственно, так же подставим в формулу (4.14) значения виртуальных перемещения (Табл.4)

(4.15)

Учитывая условие δξ=0, получим:

(4.16)

Преобразовав формулу (4.16), получим:

(4.17)

(4.18)

Где:

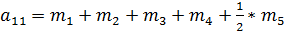(4.19)

(4.20)

Подставим значения масс (Табл.1) в формулу 4.19 и 4.20 соответственно и получим:

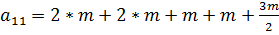(4.21)

(4.22)

 

2) Найдём работу сил инерции, учитывая, δx=0 и δξ≠0

Запишем работу аналогично формуле (4.15)

(4.23)

Учтём условие δx=0 и получим:

(4.24)

Сгруппировав слагаемые в выражении (4.24), получим:

(4.25)

(4.26)

Где:

(4.26)

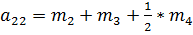(4.27)

Подставив значения масс (Табл.1), получим:

(4.28)

(4.29)

 

 

Сформулируем принцип Даламбера-Лагранжа

(4.30)

Применим принцип к нашему случаю:

(4.31)

Подставим полученные ранее данные в формулу (4.31)

(4.32)

 

 

Уравнение Лагранжа

(5.1)

Где i= 1,2,…n

n- Число степеней свободы

Получим уравнение Лагранжа для n=2

(5.2)

Возьмём первое уравнение системы и найдём неизвестные данные

Продифференцируем формулу (2.11) по и получим дифференциальное выражение кинетической энергии:

(5.3)

Продифференцируем формулу (5.3) по времени:

(5.4)

Продифференцировав выражение (2.11) по xполучим:

(5.5)

Возьмём второе уравнение системы и проделаем аналогичные действия.

Продифференцируем формулу (2.11) по и получим дифференциальное выражение:

(5.6)

 

 

Продифференцируем выражение (5.6) по времени:

(5.7)

Продифференцировав выражение (2.11) по ξ, получим:

(5.8)

Таким образом, система уравнений (5.2) примет вид:

(5.9)

Где:

(см. формулу 4.9)

(см. формулу 4.13)

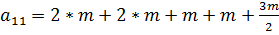(см. формулу 2.13)

(см. формулу 2.14)

(см. формулу 2.15)

Подставим данные коэффициенты в систему (5.9) и получим:

(5.10)

Примечание:

Радиусы тел учитываются в соответствие с (Рис.1)

 

 

Выразим из второго уравнения системы (5.10) координату и подставим в первое уравнение, таким образом, получим:

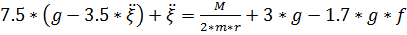(5.11)

Выражая получаем:

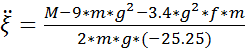(5.12)

Примем значение равное и подставим его во второе уравнение системы(5.10), тогда будет равен:

(5.13)

Примем значение равное

Таким образом, имеем:

(5.14)

(5.15)

Проинтегрируем по времени формулы (5.12) и (5.13), учитывая равенства (5.14) и (5.15)

(5.16)

Проинтегрируем выражение (5.16) по времени:

(5.17)

 

 

Учитывая начальные условия:

(1)

(2)

(3)

(4)

Найдём с₁; с₂; с₃; с₄

Подставив начальные условия в выражение (5.17) получим, что:

(5.18)

(5.19)

(5.20)

(5.21)

Подставив значения (5.18-21) в выражение (5.17) получим окончательные значения обобщённых координат:

Где и равны, соответственно, равенствам (5.15) и (5.14)