Использование свойств и графиков функций при решении уравнений и неравенств. (Функциональный метод решения уравнений и неравенств)
Одним из методов решения уравнений и неравенств является функциональный, основанный на использовании свойств функций. В отличие от графического метода, знание свойств функций позволяет находить точные корни уравнения (неравенства), при этом не требуется построения графиков функций. Использование свойств функций способствует рационализации решений уравнений и неравенств.
Рассмотрим использование некоторых свойств функций при решении уравнений и неравенств.
1. Использование понятия области определения функции
Областью определения функции у = f(x) называется множество значений переменной х, при которых функция имеет смысл.
Пусть дано уравнение f(x) = g(x), где f(x) и g(x) — элементарные функции, определенные на множествах D1, D2. Тогда областью D допустимых значений уравнения будет множество, состоящее из тех значений х, которые принадлежат обоим множествам, то есть D = D1∩D2. Ясно, что когда множество D пустое (D = Ø), то уравнение решений не имеет.
Пусть требуется решить неравенство f(x) > 0. D(f) — область определения функции f(x). Если удается доказать, что для всех х из области определения выполняется неравенство f(x) > 0, то D(f) представляет собой решение данного неравенства.
Пример 1. Решите уравнение:  +
+  =5
=5
Решение.

 ОДЗ: 1-x
ОДЗ: 1-x  0, x
0, x  1,
1,  решений нет.
решений нет.
x-3  0 x
0 x  3
3
Ответ: Ø
Пример 2. Решите уравнение: 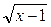 +
+  = x
= x  - 1
- 1
Решение. 
ОДЗ: x-1  0,
0,  x =1
x =1
1-x  0
0
ОДЗ состоит из одной точки x =1. Остается проверить, является ли x =1 корнем уравнения.
x =1 
 +
+  =1
=1  -1, 0=0. Верно.
-1, 0=0. Верно.
Ответ: 1
Пример 3. Решите неравенство:  +
+ 
 1
1
Решение.
1.Область определения левой части: 
 1.
1.
2.Для любого x из области определения выполняется неравенство  +
+ 
 1
1
Ответ: x  (-
(- 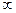 ;-1]
;-1]  [1;+
[1;+ 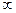 ).
).
Использование понятия области значений функции
Областью значений функции у = f(x) называется множество значений переменной у, при допустимых значениях переменной х.
Функция у = f(x) называется ограниченной на данном промежутке (содержащемся в области ее определения), если существует такое число N > 0, что при всех значениях аргумента, принадлежащих данному промежутку, имеет место неравенство  < N.
< N.
Пусть дано уравнение f(x) = g(x), где f(x) и g(x) — элементарные функции, определенные на множествах D1, D2. Обозначим область значений этих функций соответственно Е1 и Е2. Если х1 является решением уравнения, то будет выполняться числовое равенство f(x1) = g(x1), где f(x1) — значение функции f(x) при х = х1, a g(x1) — значение функции g(x) при х = х1. Значит, если уравнение имеет решение, то области значений функций f(x) и g(x) имеют общие элементы (Е1 ∩ Е2  Ø). Если же таких общих элементов множества Е1 и Е2 не содержат, то уравнение решений не имеет.
Ø). Если же таких общих элементов множества Е1 и Е2 не содержат, то уравнение решений не имеет.
Пример 1. Решите уравнение:  +
+  =2
=2
Решение.
 ОДЗ: x
ОДЗ: x  0,
0,  x
x  0
0
x+9  0
0

 0,
0, 
 3
3 
 +
+ 
 3,
3,  решений нет.
решений нет.
Ответ: Ø
 |
Пример 2. Решите неравенство:.
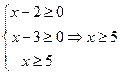 |
ОДЗ:
На ОДЗ правая часть неравенства неположительна, а левая - положительная.
Ответ: [5; +∞).
Использование свойства монотонности функции.
Функция f(x) называется возрастающей (убывающей) на данном числовом промежутке X, если большему значению аргумента х  X соответствует большее (меньшее) значение функции f(x), то есть для любых х1 и х2 из промежутка X таких, что х2 > х1 выполнено неравенство f(x2) > f(x1) (f(x2) < f(x1)).
X соответствует большее (меньшее) значение функции f(x), то есть для любых х1 и х2 из промежутка X таких, что х2 > х1 выполнено неравенство f(x2) > f(x1) (f(x2) < f(x1)).
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Рассмотрим несколько свойств монотонных функций, используемых для установления характера монотонности функций и лежащих в основе утверждений об уравнениях и неравенствах.
Теорема 1. Монотонная на промежутке X функция каждое свое значение принимает лишь при одном значении аргумента из этого промежутка.
Теорема 2. Если функция f(x) возрастает (убывает) на промежутке X и функция g(x) возрастает (убывает) на промежутке X, то функция h(х) = f(x) + g(x) + С также возрастает (убывает) на промежутке X (С — произвольная постоянная).
Теорема 3. Если функция f(x) неотрицательна и возрастает (убывает) на промежутке X, функция g(x) неотрицательна и возрастает (убывает) на промежутке X, С > 0, то функция h(х) = С ∙ f(x) ∙ g(x) также возрастает (убывает) на промежутке X.
Теорема 4. Если функция f(x) возрастает (убывает) на промежутке X, то функция – f(x) убывает (возрастает) на этом промежутке.
Теорема 5. Если функция f(x) монотонна на промежутке X и сохраняет на этом множестве знак, то функция  на промежутке X имеет противоположный характер монотонности.
на промежутке X имеет противоположный характер монотонности.
Теорема 6. Если обе функции f(x) и g(x) возрастающие или обе убывающие, то функция h(х) = f(g(x)) — возрастающая функция. Если одна из функций возрастающая, а другая убывающая, то h(х) = f(g(x)) — убывающая функция.
Теоремы об уравнениях и неравенствах.
Теорема 7. Если функция f(x) монотонна на промежутке X, то уравнение f(x) = С имеет на промежутке X не более одного корня.
Теорема 8. Если функция f(x) монотонна на промежутке X, то уравнение f(g(x)) = f(h(x)) равносильно на промежутке X уравнению g(x) = h(x).
Теорема 9. Если функция f(x) возрастает (убывает) на промежутке X, то неравенство
f(g(x)) < f(h(x)) равносильно на промежутке X неравенству g(x) < h(x) (g(x) > h(x)).
Аналогичное свойство имеет место и для нестрогих неравенств.
Теорема 10. Если функция f(x) возрастает на промежутке X, а g(x) убывает на промежутке X, то уравнение f(x) = g(x) имеет на промежутке X не более одного корня.
Теорема 11. Если функция f(x) возрастает на промежутке X, то уравнение f(f(x)) = х равносильно на промежутке X уравнению f(x) = х
Пример 1. Решите уравнение: 
Решение.
ОДЗ: 
Функция 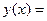 х 2 +
х 2 +  убывает на промежутке (-
убывает на промежутке (- 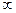 ;-0], а
;-0], а  - постоянная функция.
- постоянная функция.
Подбором находим, что x =- - 4. В силу теоремы 7, найденный корень единственный.
Ответ: - 4.
Пример 2. Решите уравнение: 
Решение.
 - функция убывает на
- функция убывает на  ;
;
 - функция возрастает.
- функция возрастает.
Подбором находим, что  .
.
В силу теоремы 10 утверждаем, что  единственный корень уравнения.
единственный корень уравнения.
Ответ: 3
Пример 3. Решите уравнение: x3 + 33 = - 2х
Решение.
ОДЗ уравнения: х є R.
Функция у(х) = x3 + 33 - возрастает на R,
Функция g(х) = - 2х - убывает на R.
Значит уравнение имеет не более одного корня.
Подбором x = -3.
Ответ: -3.
Пример 4. Решите уравнение: x5 + x3 + х = - 42
Решение.
ОДЗ: х є R.
Функция у(х) = x5 + x3 + х - возрастает на R,
Функция g(х) = - 42 постоянна на R.
Значит уравнение имеет не более одного корня.
Подбором x = -2.
Ответ: -2.
Пример 5. Решите уравнение:  = 8 -2х
= 8 -2х
Решение.
ОДЗ: х  - 1.
- 1.
Левая часть уравнения задает возрастание, а правая - убывание функции.
Значит, это уравнение имеет не более одного корня.
Подбором x = 3.
Ответ: 3.