Передаточная функция звена, охваченного обратной связью

Обратной связью называется цепь передачи воздействий с выхода звена (системы) на ее вход. Наряду с главной обратной связью, с помощью которой реализуется принцип управления по отклонению, в САУ для повышения точности часто применяются местные обратные связи, охватывающие одно или несколько звеньев (рис. 2.6). Обратные связи бывают отрицательные и положительные. При отрицательной обратной связи воздействие поступающее на вход звена в прямой цепи, равно разности воздействий а при положительной — их сумме:

Последнее выражение называется уравнением замыкания контура.

Для получения уравнения звена с обратной связью запишем уравнения звеньев в прямой цепи и цепи обратной связи:

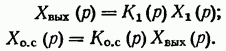
Значение из (2.43) подставляем в (2.41):

а полученное значение в (2.42):

или

Из этого уравнения определяем передаточную функцию звена с

Рис. 2.6. Схема звена, охваченного обратной связью.

обратной связью:

где знак соответствует отрицательной, а — положительной обратной связи.

Если окажется, что в некоторой области значений произведение то выражение (2.45) для этих значений может быть записано в виде Кохв т. е. передаточная функция звена, охваченного обратной связью, равна величине, обратной передаточной функции звена, включенного в цепь обратной связи. Поэтому изменение параметров звена в прямой цепи мало влияет на Кохв

В случае, если в обратной связи отсутствует какое-либо звено, т. е.. имеет место единичная обратная связь

Используя полученные выражения передаточных функций типовых соединений звеньев, можно сложную структурную схему системы привести к схеме, состоящей из ряда последовательно включенных звеньев и тем сайым облегчить определение передаточной функции системы.

 

 

23. Передаточные функции систем автоматического регулирования.

 

24. Основные группы показателей для оценки качества регулирования. Рассмотрим основные показатели качества систем автоматического регулирования, пользуясь характеристикой переходного процесса отработки единичного воздействия показанной на рис. XII.1. В точке А переходного процесса, соответствующей времени имеет место максимальное отклонение регулируемой величины .

Рис. XII.1 Характеристики переходного процесса при типовом единичном возмущении

Под первым показателем качества понимают величину

где соответствует установившемуся значению регулируемой величины, т. е. 4

Обычно в теории регулирования стшах именуют максимумом перерегулирования.

Второй показатель качества позволяет оценить быстродействие системы автоматического регулирования

и называется временем регулирования (протекания переходного процесса) 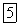Учитывая, что полное затухание в системе происходит лишь условно принимают за момент окончания переходного процесса точку пересечения графика этого процесса с линиями, соответствующими -ному отклонению от установившегося значения.

Третий показатель качества характеризует число колебаний регулируемой величины в течение времени переходного процесса

Наряду с этими основными показателями качества при проектировании систем автоматического регулирования часто используют следующие характеристики.

Собственная частота колебаний системы

где — период собственных колебаний системы.

Логарифмический декремент затухания системы характеризующий быстроту затухания колебательного процесса:

где и — две амплитуды для рядом расположенных экстремумов кривой переходного процесса. Чем больше логарифмический декремент затухания, тем быстрее происходит затухание переходного процесса.

Максимальная скорость отработки регулируемой величины

Для каждой системы регулирования, имеющей колебательный переходный процесс, на основе указанных критериев качества можно установить область допустимых отклонений регулируемой величины.

В системах автоматического регулирования возможны переходные процессы, характер протекания которых отличен от указанного на рис. XII. 1. Все многообразие переходных процессов в этих системах можно разделить на четыре группы:

колебательный процесс, характеризуемый несколькими значениями перерегулирований, превышающими 5% зоны установившегося значения (кривая 1 на рис. XII.2);

переходный процесс с одним перерегулированием (кривая 2);

монотонный процесс (кривая 3), когда скорость изменения регулируемой величины не меняет знака в течение всего времени при

процесс без перерегулирования, когда с точностью до А при всех (кривая 4 на рис. XII.2).

 

 

25. Оценка точности линейных САР.

 

26. Понятие статического и астатического звена, статической и астатической системы.

27. Понятие устойчивости. Условие устойчивости линейных систем. Критерий устойчивости Гурвица. Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменении его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.

Необходимое и достаточное условие устойчивости формулируется следующим образом: Звено или система называются устойчивыми, если переходная составляющая с течением времени стремится к нулю:

Критерий Гурвица, как и критерий Стодола, определяет устойчивость по характеристическому полиному системы без непосредственного вычисления его корней. Однако критерий Стодола является необходимым критерием устойчивости, но не является достаточным. То есть, если по критерию Стодола система неустойчива, то она действительно является неустойчивой, если по критерию система устойчива, то для подтверждения ее устойчивости требуются дополнительные расчеты. Например, характеристический полином s³ + s² + 2s + 8

по критерию Стодола соответствует устойчивой системе, однако корни этого полинома равны s₁ = -2, s_2,3 = 0,5 ± j×1,94. То есть система фактически является неустойчивой, хотя коэффициенты полинома положительны.

Критерий Гурвица дает необходимое и достаточное условие устойчивости линейных систем.

Исходной информацией для данного критерия является характеристический полином системы: разомкнутой A(s) или замкнутой D(s) – в зависимости от того, какая система анализируется.

Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с a_n+1 по a₀. Справа и слева от нее записываются коэффициенты с индексами через 2 (a₀, a₂, a₄… или a₁, a₃, a₅ …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.

Если хотя бы один определитель будет равен нулю, то система будет находиться на границе устойчивости.

Если хотя бы один определитель будет отрицателен, то система неустойчива независимо от числа положительных или нулевых определителей.

 

 

28. Критерий устойчивости Найквиста. Запасы устойчивости. Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой (а. ф. х.) или логарифмических частотных характеристик (л. ч. х.) разомкнутой системы.Помимо исследования устойчивости по виду указанных характеристик можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы. Для нормального функционирования всякая САР должна быть достаточно удалена от границы устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена прежде всего следующими причинами: а) уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы; б) при линеаризации уравнений погрешности приближения дополнительно увеличиваются; в) параметры элементов определяют с некоторой погрешностью; г) параметры однотипных элементов имеют технологический разброс; д) при эксплуатации параметры элементов изменяются вследствие старения.Следовательно, устойчивая по расчету САР в действительности может оказаться неустойчивой. В следящих системах запас устойчивости необходим еще и для хорошего качества регулирования (см. гл. 7).О запасе устойчивости можно судить по расположению корней характеристического уравнения системы: чем дальше отстоят они от мнимой оси (в левой полуплоскости), тем больший запас устойчивости. Каждый критерий устойчивости также позволяет определять запас устойчивости.Количественная оценка запаса устойчивости зависит от того, какой критерий устойчивости выбран. В практике инженерных расчетов наиболее широко используют определение запаса устойчивости на основании критерия Найквиста, по удалению

АФЧХ разомкнутой системы от критической точки с координатами что оценивают двумя показателями: запасом устойчивости по фазе y и запасом устойчивости по модулю (по амплитуде)

 

 

29. Оценка качества переходных процессов по переходным функциям прямым методом. Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая переходного процесса Y (t). Еще совсем недавно применение этого метода было ограничено из-за трудностей получения переходных процессов. В настоящее время переходный процесс даже очень сложной системы можно получить путем моделирования на ЭВМ. Поэтому значение прямого метода существенно возросло.

Качество переходных процессов обычно оценивают при ступенчатых воздействиях. Для линейных систем ¾по переходно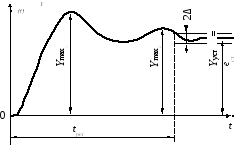й функции.

Рассмотрим основные показатели качества при их оценке по переходной функции.

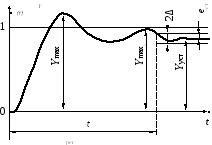
Возможный вид переходных функций по управляющему и возмущающему воздействиям приведен на рис.

Пример переходной функции САР по управляющему воздействию

Пример переходной функции САР по возмущающему воздействию

1. Отклонение регулируемой величины от своего установившегося значения характеризуется следующими показателями.

Для переходной функции по управляющему воздействию определяется перерегулирование:

%,

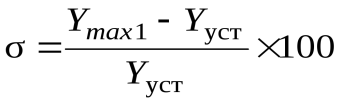где Y _max1 ¾максимальное значение регулируемой величины в переходном процессе; Y _уст¾установившееся значение регулируемой величины.

Если нет специальных требований к системе, то нормальным считается перерегулирование s < 30 %. Перерегулирование характеризует запас устойчивости системы. При s < 30 % в большинстве случаев запас устойчивости достаточен.

Для переходных процессов по возмущающему воздействию определяется максимальное отклонение регулируемой величины от установившегося значения, приходящееся на единицу возмущающего воздействия F(t):

%

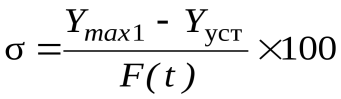2. Быстродействие системы оценивается временем регулирования. Время регулирования t _рег определяется как интервал времени от начала переходной функции до момента, когда отклонение регулируемой величины от ее нового установившегося значения становится меньше определенной достаточно малой величиныD:

½ Y(t) -‑ Y _уст½ < D.

Обычно в качестве Dберут от 1 до 5 % от нового установившегося значения регулируемой величины для переходной функции по управляющему воздействию или от 1 до 5 % от максимального отклонения регулируемой величины для переходной функции по возмущающему воздействию.

3. Колебательность переходного процесса определяется числом N перерегулирований для переходной функции по управляющему воздействию или числом колебаний N для переходной функции по возмущающему воздействию за время переходного процесса.

Для рассматриваемого примера N = 1.

Обычно приемлемым числом колебаний считается N < 2...3.

Колебательность также оценивается отношением соседних отклонений регулируемой величины от установившегося значения:

С = (Y _max2 − Y _уст)/(Y _max1 − Y _уст).

Эта величина так и называется колебательностью. Чем меньше колебательность, тем лучше считается качество управления.

Иногда колебательность оценивается декрементом затухания . Применяются и другие оценки декремента затухания, например отношение соседних отклонений от Y _уст.

Перерегулирование и максимальное отклонение регулируемой величины от установившегося значения также служат оценкой колебательноти.

4. По переходным функциям может быть определена также и статическая ошибка системы по управляющему и возмущающему воздействиям:

е _ст= Y _з− Y _уст,

где Y _з ¾ заданное значение регулируемой величины (для нашего примера Y _з = 1 для переходной функции по управляющему воздействию, Y _з=0 для переходной функции по возмущающему воздействию).

Статическая ошибка характеризует точность системы, но не качество переходных процессов. Здесь ее определение упомянуто в связи с рассмотрением прямого метода оценки качества регулирования.

 

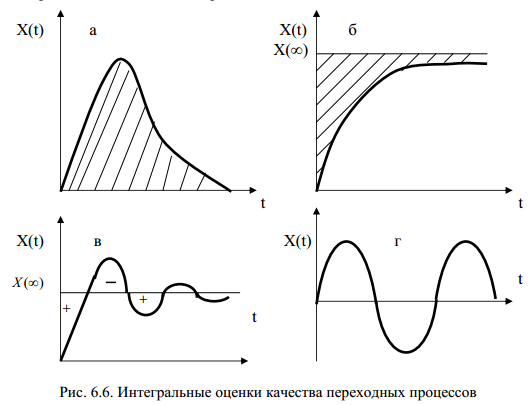
30. Интегр альные критерии качества переходных процессов.

 

 

31. Типовые законы регулирования. Задача регулятора - определение текущей ошибки регулирования и генерация соответствующего регулирующего воздействия, направленного на устранение этой ошибки.

Закон регулирования – зависимость между входной и выходной величинами регулятора составленного без учета инерционности его элементов

Существует всего 5 основных типов регуляторов:

• Пропорциональный
• Интегральный
• Пропорционально-Интегральный (изодромный)
• Пропорционально-Дифференциальный
• Пропорционально-Интегрально-Дифференциальный

 

 

32. Понятие нелинейной системы. Существенно нелинейные и несущественно нелинейные звенья.

33. Типовые нелинейные звенья.

34. Понятие о дискретных системах, их классификация по виду дискретизации сигнала.

35. Понятие импульсной и цифровой системы. Достоинства импульсных и цифровых систем.

36. Понятие позиционной системы. 2-х позиционная система и режим ее работы.

37. Понятие позиционной системы. 3-х позиционная система и режимы ее

работы.

38. Понятие технических средств автоматизации. Их классификация.

39. Понятия первичного измерительного преобразователя и датчика. Типовой

функциональный состав датчиков.

40. Классификация датчиков.

41. Статическая и динамическая характеристики датчиков.

42. Омические первичные преобразователи: потенциометрические, тензометрические.

43. Электромагнитные первичные преобразователи.

44. Емкостные первичные преобразователи.

45. Фотоэлектрические первичные преобразователи.

46. Датчики температуры: биметаллические, термометры сопротивления металлические и полупроводниковые (термисторы, позисторы).

47. Датчики положения и уровня.

48. Датчики давления, расхода и количества. Датчики скорости.

49. Датчики влажности.

50. Датчики состава и свойства веществ.

51. Понятие исполнительного устройства, исполнительного механизма,

регулирующего органа.

52. Электродвигательные и электромагнитные исполнительные механизмы.

53. Пневматические и гидравлические исполнительные механизмы.

54. Понятие релейного устройства.

55. Классификация электрических реле, их принципы действия.

56. Параметры реле. Эксплуатационные параметры контактов реле.

57. Электромагнитные реле.

58. Магнитоуправляемые контакты (герконы).

59. Реле выдержки времени и программные реле.

60. Конечные (путевые) выключатели.

61. Контакторы и магнитные пускатели.

62. Дискретизация сигнала по времени и уровню. Понятие о дискретных системах автоматического управления и их классификация по виду дискретизации (квантования) сигнала.

63. Представление информации в цифровом виде. Преобразование аналоговой информации в цифровую и обратно. Разрядность.

64. Цифровые системы. Функциональный состав цифровых систем. Достоинство цифровых систем и перспективы их развития.

65. Архитектура микропроцессорных устройств.

66. Принципы работы микропроцессорной системы.

67. Классификация контроллеров. Применение контроллеров для автоматизации технологических процессов.

68. Структура современных контроллеров. Базовый блок. Блок расширения. Модуль расширения. Дополнительные модули контроллеров: аналоговые модули, счетные модули, интерфейсные модули.

69. Назначение модулей, их технические характеристики и схемы подключений.

70. Программное обеспечение контроллеров.

71. Операционные системы реального времени.

72. Системы и языки программирования.

73. Организация алгоритмов управления в программном виде.

74. Логические основы программирования.

75. Современные интерфейсы для связи микропроцессорных систем управления.

76. Последовательная и параллельная передача данных.

77. Современные протоколы передачи информации (RS-232, RS-485, CAN, USB и др.).

78. Принципы построения сети микропроцессорных устройств управления.