При эксплуатации на системы и их отдельные элементы (звенья) действуют различные внешние воздействия. Наиболее часто изучают реакцию систем и звеньев на типовые воздействия, являющиеся математическими моделями наиболее часто встречающихся реальных воздействий.
В качестве типовых используют следующие воздействия. 1. Ступенчатое воздействие:2. Импульсное воздействие (дельта-функция):3. Гармоническое воздействие:Временные характеристикиРеакция системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией. Переходная функция обычно обозначается h(t). Если ступенчатое входное воздействие неединичное 1 (t) × а, то ординаты переходной функции увеличиваются в а раз, что следует из принципа суперпозиции для линейных систем и звеньев. Реакция системы (звена) на импульсное воздействие (d - функцию) при нулевых начальных условиях называется импульсной переходной функцией или функцией веса. Функция веса обычно обозначается W(t). Переходные функции и функции веса получают путем решения дифференциальных уравнений, описывающих системы (звенья) при ступенчатых и импульсных воздействиях, по их передаточным функциям и путем моделирования на ЭВМ. Они могут быть получены также экспериментально (импульсную переходную функцию получают как реакцию на короткий импульс).Возможный вид переходных и импульсных переходных функций приведен на рис. 2.9.1 и 2.9.2.
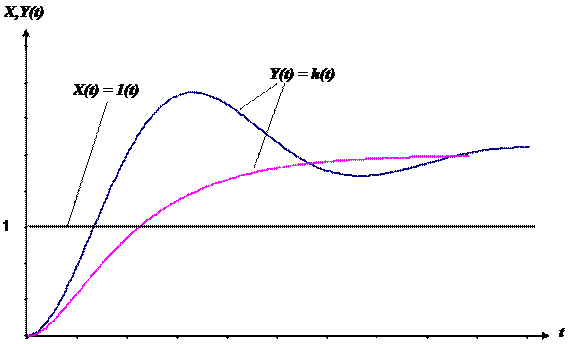
Рис. 2.9.1 Возможный вид переходных функций
Свойства линейных систем (звеньев) таковы, что частоты входных и выходных сигналов одинаковы. Амплитуда выходного сигнала при постоянной амплитуде входного сигнала и разность фаз между входным и выходным сигналами зависит только от частоты.Реакция системы (звена) на гармоническое воздействие характеризуется его частотными характеристиками. Амплитудной частотной характеристикой (АЧХ) называется зависимость отношения амплитуд выходного и входного гармонических сигналов от частоты в установившемся режиме:
|
|
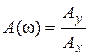. (2.9.12)
Фазовой частотной характеристикой (ФЧХ) называется зависимость разности фаз j(w) между входным и выходным сигналами от частоты в установившемся режиме.
Для теоретического получения АЧХ и ФЧХ систем и звеньев используют их частотные передаточные функции, поскольку модуль А( w ) частотной передаточной функции системы или звена является АЧХ этой системы или звена, а аргумент j ( w ) частотной передаточной функции системы или звена является ФЧХ этой системы или звена.
17. Типовые воздействия. Процессы в системе автоматического управления возникают под влиянием внешних воздействий на систему. Внешними воздействиями явлются управляющие воздействия (или возмущения). В реальных условиях внешние воздействия могут иметь произвольный характер и выражаться произвольными функциями времени, как детерминированными, так и статистическими. Поскольку в этом случае задача исследования становится неопределенной, то при анализе систем автоматического управления используют ряд типовых воздействий, которые позволяют наиболее полно выявить динамические свойства исследуемой системы и в то же время наиболее близки к реальным внешним воздействиям.В теории автоматического управления используются следующие типовые воздействия при изучении переходных процессов в системе.1. Ступенчатая функция (скачкообразное воздействие)График ступенчатой функции приведен на рис. 14. В нулевой момент времени воздействие скачком изменяется от нуля до некоторой постоянной величины. Аналитическое выражение для ступенчатой функции
|
|
При значении функции, равном единице (рис. 14), функция называется единичной ступенчатой функцией. Единичную функцию обозначают
x(t) = 1(t) = [1].
Если амплитуда ступенчатой функции отличается от единицы и равна некоторой величине А, то такая функция является неединичной и обозначается
x(t) = A[1].
Изображения Лапласа для ступенчатой функци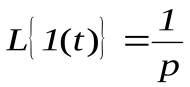и
и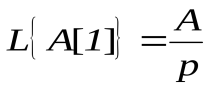 
.
2. Единичная импульсная функция, или дельта-функция
Эта функция представляет собой производную от единичной ступенчатой функции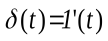 
.
Дельта-функция равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности (рис. 15).
Основное свойство дельта-функции
,
т.е. её график имеет единичную площадь.
Размерность единичной дельта-функции [сек–1]. Дельта-функцию можно рассматривать как предел прямоугольного импульса при стремлении его длительности к нулю, а амплитуды – к бесконечности. С помощью импульсной функции удобно моделировать ударные воздействия на систему (кратковременные воздействия – удары).
2. Гармоническая функция
Функция, изменяющаяся по гармоническому закону (закону синуса или косинуса), рис. 16.
или 
.
В теории автоматического управления гармоническую функцию часто записывают с использованием формулы Эйлера
.
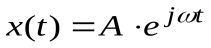Гармоническая функция применяется при исследовании частотных свойств элементов и систем автоматического управления. С её помощью моделируются повторяющиеся периодические воздействия (например, вибрации).
|
|
2. Степенные функции времени
В 
ыражают линейное, квадратичное и т.д. изменение входной величины во времени:
,
где k– постоянный коэффициент;a– константа.
При a=1 обеспечивается линейная функция времени, график которой приведен на рис. 17.
Степенные функции применяются в том случае, когда необходимо смоделировать непрерывное изменение воздействия на систему, например при исследовании следящих систем.
18. Временные (переходные) характеристики линейных систем и звеньев (общие понятия). Временной или импульсной характеристикой динамического звена называют реакцию звена на, обозначая ее как. При этом схема эксперимента имеет вид – вид -
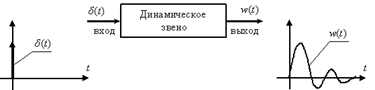
Рис. 4
Для этого рассмотрим динамическое звено с передаточной функцией
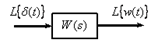
Рис. 5
В этом случае, в соответствии с (5), имеем
.
Таким образом
Получаем, что передаточная функция звена - это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции
,
при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
,
а если легко получить, тогда
.
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на, обозначая ее как. При этом схема эксперимента имеет вид -
Рис. 6
Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
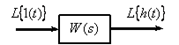
Рис. 7
В этом случае, в соответствии с (5), имеем
.
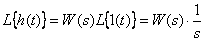
По теореме об интегрировании оригинала имеем
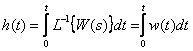
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
.
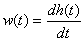
Переходная характеристика динамического звена может быть определена по передаточной функции
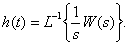
динамический дифференциальный уравнение управление
Контрольные вопросы и задачи
1. Что такое линейное динамическое звено?
2. Как определить передаточную функцию линейного динамического звена?
3. Перечислите основные элементы структурных схем систем управления.
4. Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
5. Как по переходной характеристике определить импульсную характеристику динамического звена?
6. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
.
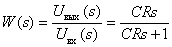
7. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
.
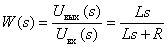
8. По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
19. Частотные характеристики линейных систем и звеньев (общие понятия).
Временными характеристиками удобно пользоваться при определении характера переходного процесса в системах автоматического регулирования. Однако в реальных системах очень часто входной сигнал изменяется по гармоническому закону заданной амплитуды и частоты. При исследовании САР ставится задача нахождения параметров колебаний на выходе системы по известным параметрам колебаний на входе. Решение этой задачи с помощью временных характеристик представляет определенные трудности. Рассматриваемый ниже частотный метод позволяет получить реакцию звена (системы) на любой периодический сигнал.
Допустим, что сигнал, поступающий на вход звена с передаточной функцией 
изменяется по гармоническому закону
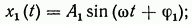
где 
— амплитуда входного сигнала; 
— круговая частота 
— начальная фаза входного сигнала.
Требуется определить выходной сигнал звена в установившемся режиме.
Используя линейное дифференциальное уравнение (2.57) и выражение (2.119), запишем
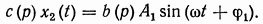
При нулевых начальных условиях решение этого уравнения в форме преобразования Лапласа будет иметь вид
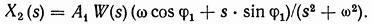
Если передаточная функция (2.93) является правильной дробью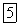 
то и 
также правильная дробь. Поэтому по теореме разложения
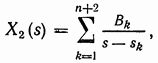
где 
— коэффициенты разложения; 
— корни уравнения с 
Решение (2.122) справедливо при отсутствии в характеристическом уравнении кратных корней.
Коэффициенты разложения 
могут быть найдены по формуле
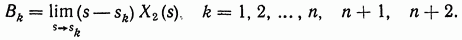
Определим коэффициенты 
приняв, что 
Тогда
Подставив в это выражениеформулу (2.121), будем иметь
Так как 
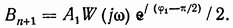
Выражение для
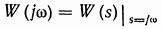
можно представить в показательной форме:
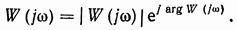
Окончательно получим
Выполнив аналогичные вычисления, можно убедиться в том, что 
коэффициент 
является комплексно-сопряженным коэффициенту 
Переход от изображений к оригиналам позволяет записать
выражение (2.122) в виде 
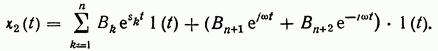
Первое слагаемое выражения (2.123) характеризует переходный процесс, второе — установившийся. В устойчивых звеньях переходный процесс с течением времени затухает 
поэтому
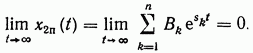
Учитывая, что 
искомую составляющую установившегося процесса представим в виде
Подставив в это выражение значение коэффициента 
получим:
Из (2.124) видно, что в итоге на выходе линейного звена устанавливаются гармонические колебания той же частоты 
амплитуда которых
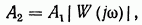
а начальная фаза
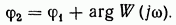
Таким образом, 
зависят от частоты входного сигнала 
При прохождении гармонического сигнала через устойчивое линейное звено изменяется его амплитуда и начальная фаза. Для неустойчивого звена приведенные выкладки теряют физический смысл. Входной и выходной сигналы звена показаны на рис. 2.12, из которого видно, что на выходе звена сигнал смещен по фазе (принято 
и имеет другую амплитуду. Искаженный вид начального участка выходного сигнала объясняется влиянием переходного процесса.
Рис. 2.12. Входной и выходной гармонические сигналы линейного звена
Формулы (2.125) и (2.126) показывают, что для определения установившейся реакции звена с передаточной функцией 
на гармонический входной сигнал достаточно знать комплексную функцию 
вещественного переменного 
Функция
получающаяся при замене в передаточной функции 
на 
называется частотной передаточной функциейзвена и может быть представлена в нескольких видах. Так, например,
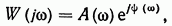
где
кроме того,
где
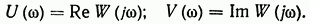
Функция 
называется амплитудной частотной характеристикой 
а функция 
— фазовой частотной характеристикой 
звена. Функции 
называются вещественной и мнимой частотными характеристиками звена.
Для каждого фиксированного значения 
частотная передаточная функция на плоскости 
может быть изображена вектором 
отклоненным от положительного направления оси абсцисс на угол 
. Годограф этого вектора при изменении частоты от 0 до 
называется амплитудно-фазовой частотной характеристикой (а.ф.х.) звена.
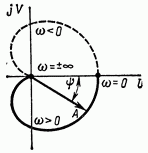
Рис. 2.13. Амплитудно-фазовая частотная характеристика звена
Из выражения (2.125) видно, что модуль вектора 
равен отношению амплитуд выходного (2.124) и входного (2.119) сигналов. Угол отклонения вектора от вещественной оси может быть найден из формулы (2.126): 
. А.ф.х. строится по точкам при задании различных значений частоты в диапазоне от 0 до 
На рис. 2.13 представлена одна из возможных форм а.ф.х. линейного звена. Зеркальное отображение этой характеристики в верхней полуплоскости объясняется тем, что замена в передаточной функции 
на 
дает сопряженные комплексные числа. Указанная на этом рисунке штриховой линией часть а.ф.х. не имеет физического смысла, однако в некоторых случаях она представляет теоретический интерес.
Построению частотных характеристик 
должен предшествовать подготовительный этап некоторых преобразований. Представив частотную передаточную функцию (2.127) в виде
где 
— вещественные части числителя и знаменателя; 
и 
— мнимые части числителя и знаменателя, можно записать
Чтобы определить 
достаточно числитель и знаменатель функции (2.127) умножить на комплексное выражение, сопряженное знаменателю:
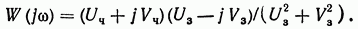
Из этого выражения получим
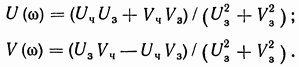
Амплитудная, фазовая, вещественная и мнимая частотные характеристики, построенные по точкам, представлены на рис. 2.14, а, б и 2.15, а, б.
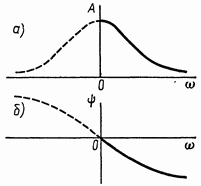
Рис. 2.14. Амплитудная (а) и фазовая (б) частотные характеристики звена
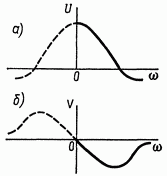
Рис. 2.15. Вещественная (а) и мнимая (б) частотные характеристики звена
При практических расчетах предпочтительнее пользоваться выражениями (2.130) и (2.131), а не (2.132) и (2.133), поскольку первые значительно проще и имеют вполне определенный физический смысл. Кроме того, характеристики 
могут быть получены экспериментально [10, 13].
20 Понятие типового звена. Виды типовых звеньев и их характеристики.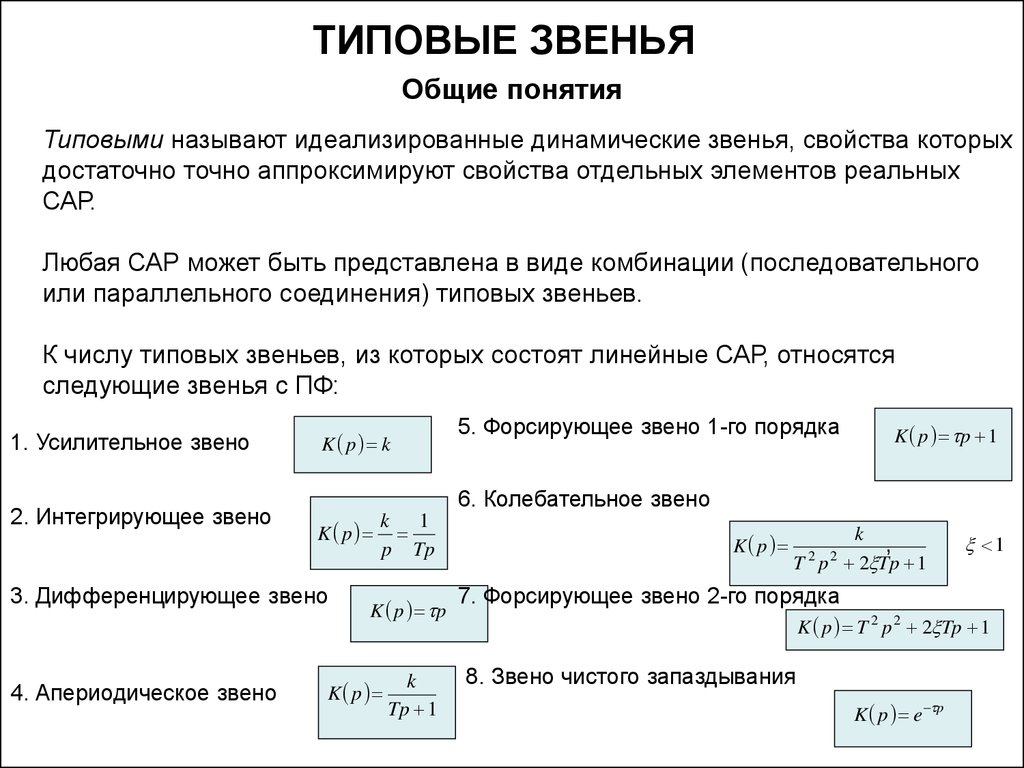 
.
21. Обратные связи. Обра́тная связь в технике — это процесс, приводящий к тому, что результат функционирования какой-либо системы влияет на параметры, от которых зависит функционирование этой системы. Другими словами, на вход системы подаётся сигнал, пропорциональный её выходному сигналу (или, в общем случае, являющийся функцией этого сигнала). Часто это делается преднамеренно, чтобы повлиять на динамику функционирования системы.
Различают положительную и отрицательную обратную связь. Отрицательная обратная связь изменяет входной сигнал таким образом, чтобы противодействовать изменению выходного сигнала. Это делает систему более устойчивой к случайному изменению параметров. Положительная обратная связь, наоборот, усиливает изменение выходного сигнала. Системы с сильной положительной обратной связью проявляют тенденцию к неустойчивости, в них могут возникать незатухающие колебания, то есть система становится генератором
22. Передаточные функции соединений звеньев. Перенос воздействий. Приведение структурных схем к одноконтурному виду. Передаточная функция последовательного соединения звеньевДля определения передаточной функции последовательного соединения звеньев с передаточными функциями (рис. 2.5, а) составляем уравнения звеньев в операционной форме
Исключив из этих уравнений все промежуточные переменные, кроме получим уравнение соединения:
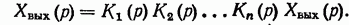
Из этого уравнения определяем передаточную функцию соединения
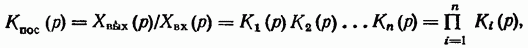
т. е. передаточная функция последовательного соединения звеньев равна произведению передаточных функций звеньев, входящих в это соединение.