Изучаемый объект или процесс весьма часто находится под действием множества факторов, форма влияния которых или неизвестна, или слишком сложна для решения в рамках конкретной задачи. Кроме того, не любой из этих влияющих факторов доступен для контроля. В этом случае для изучения применяют статистические методы. Суть этих методов заключается в том, что изучается не единичное явление, а массовая совокупность однородных явлений. В такой массовой совокупности влияние каждого второстепенного фактора носит случайный характер и в общей массе взаимно погашается. В результате проявляются общие для всей совокупности статистические закономерности. Если нас интересует некоторый количественный или качественный признак, то подвергают наблюдению множество объектов, характеризующихся этим признаком. Если наблюдению подвергаются абсолютно все объекты – носители этого признака, то наблюдение называют сплошным (перепись населения). В силу множества причин (временные, материальные и т. д.) наблюдению чаше всего подвергают определенную часть объектов, отобранных по специальным правилам. В этом случае наблюдение называют выборочным. Целью статистического наблюдения является изучение изменения вариации признака в данной совокупности.
Занятие 1. ПОСТРОЕНИЕ
СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ВЫБОРКИ.
ГРАФИК СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
Произвольное множество однородных объектов называют генеральной совокупностью. Множество случайно отобранных из генеральной совокупности объектов называют выборочной совокупностью или выборкой.
Число объектов совокупности называют объемом совокупности. Объем генеральной совокупности обозначают N, а выборочной – n.
Пусть для изучения количественного признака Х из генеральной совокупности извлечена выборка объема n. Первичным результатом статистического наблюдения является перечень членов выборочной совокупности и соответствующих им значений признака. Значения признака иначе называют вариантами. Такая сводка называется рядом вариант или простым статистическим рядом. Простой статистический ряд можно подвергнуть первичной обработке, заключающейся в группировке данных членов совокупности. Если количественный признак дискретный (принимает множество определенных значений), то при группировке выбирают члены совокупности, принимающие одни и те же значения. В результате группировки приходят к таблице.
Таблица 1
| Значения признака хi | x1 | x2 | x3 | … | xk | Итого |
| Число объектов | n1 | n2 | n3 | … | nk | n |
Число ni значений признака хi называют частотой соответствующего значения хi. Очевидно, что 
ni = n, где n – объем выборки.
Перечень вариантхi и соответствующих им частот ni носит название статистического распределения выборки, заданного в табличном виде.
Если количественный признак принимает любые значения из некоторого интервала, то его считают непрерывным. При группировке данных в этом случае все значения разбивают на интервалы и подсчитывают, сколько значений признака попадает в каждый интервал. Статистическое распределение выборки принимает вид:
Таблица 2
| Интервалы | (x0, x1) | (x1, x2) | … | (xk-1, xk) | Итого |
| Число значений признака | n1 | n2 | … | Nk | n |
Отношение ni/n называют относительной частотой и обозначают wi. Очевидно, 
wi= 1.
Замечание 1. Кроме статистических распределений, заданных в виде таблиц 1 и 2, можно получить статистические распределения относительных частот в виде следующих таблиц:
Таблица 3
| Значение признака | x1 | x2 | … | xk | Итого |
| Относительная частота | w1 | w2 | … | wk | n |
Таблица 4
| Интервалы | (x0, x1) | (x1, x2) | … | (xk-1, xk) | Итого |
| Относительная частота | w1 | w2 | … | wk |
Замечание 2. При составлении статистического распределения в виде таблиц 2 и 4 частоту вариант, точно попавших на границы интервалов, делят поровну между ними или относят к левому (правому) интервалу. Выбор типа отнесения произволен, но он должен быть единообразным для всей выборки.
Для наглядного представления статистических распределений признака строят полигон для дискретного признака или гистограмму для непрерывного распределения признака.
Полигоном частот (относительных частот) называют ломаную с вершинами в точках (xi, ni) или (xi, wi).
Гистограммой частот (относительных частот) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной (xi+1 - xi), а высотами величины ni/(xi+1 - xi) или wi/(xi+1 - xi).
Пример 1.1. Построить статистическое распределение выборки и изобразить его графически для следующего распределения размеров 45 пар мужской обуви, проданных магазином за день.
39 41 40 42 41 40 42 44 40 43 42 41 43 3942 41 42 39 41 37 43 41 38 43 42 41 40 41 38 44 40 39 41 40 42 40 41 42 40 43 38 39 41 41 42
Решение
Сгруппируем данные, расположив их в порядке возрастания, и подсчитав, сколько раз встречалось каждое значение признака, получим следующее статистическое распределение в табличном виде.
| Размер обуви | Итого | ||||||||
| Число пар |
Изобразим полученное распределение графически. Графиком распределения будет полигон.
37 38 39 40 41 42 43 44
Пример 1.2. Выработка валовой продукции на одного работающего за год по деревообрабатывающим предприятиям составила (тыс. сом).
5.0 4.0 3.9 7.4 4.5 5.3 5.6 7.3 3.8 5.2 5.1 6.3 5.5 4.8 5.1 7.2 4.1 6.5 5.4 5.8 6.0 6.4 5.8 5.3 4.9 6.2 7.2 5.9 5.7 5.5
Составить статистическое распределение выборки и изобразить его графически.
Решение
Признак принимает любые значения от 3.8 до 7.4. Разобьем весь интервал на 9 частичных интервалов с одинаковой длиной h = (7.4-3.8)/9 = = 0.4 и подсчитаем, сколько значений признака попадает в каждый частичный интервал (значения, совпадающие с граничными, будем относить к левому интервалу). Статистическое распределение частот оказывается следующим в табличном виде.
| Интервалы | 3.8-4.2 | 4.2-4.6 | 4.6-5.0 | 5.0-5.4 | 5.4-5.8 | 5.8-6.2 | 6.2-6.6 | 6.6-7.0 | 7.0-7.4 | Итого |
| Количество значений |
Графиком полученного распределения будет гистограмма.
Завдания
1.1. Число рабочих мест в магазинах составляло:
2 5 4 3 2 1 2 3 4 2 3 2 2
2 2 1 3 4 3 2 3 1 2 3 3 3
2 2 4 1
Составить статистическое распределение частот и изобразить его графически.
1.2. Данные о возрасте 56 студентов первого курса оказались следующими (приводится число полных лет):
17 17 18 17 18 17 19 17 20 19 17 18 20
18 17 20 21 20 17 18 22 18 17 18 17 18
19 17 22 19 21 19 21 18 17 21 21 17 19
18 20 17 18 19 19 17 18 19 17 20 17 18
18 18 20 17
Построить статистическое распределение и изобразить его графически.
1.3. Результаты хронометража при выполнении одной и той же операции 20 рабочими оказались следующими (длительность операции задается в минутах):
42 56 45 51,5 43 47 49,5 47,5 51 49 45,5 52,3 53
48 46,5 44 50 47,5 55,5 45
Построить интервальный ряд с пятью равными интервалами и изобразить его графически.
1.5. По имеющимся данным о возрасте рабочих одной строительной организации (приводится число полных лет):
25 17 53 18 19 46 18 35 25 23 22 25 17
23 35 21 26 19 17 22 18 25 27 44 35 25
24 25 17 24 18 23 32 23 33 26 18 27 38
28 18 18 17 21 18 19 22 42 22
Составить статистическое распределение частот и изобразить его графически.
1.56. По данным измерения диаметра валиков (в см) построить статистическое распределение относительных частот и изобразить его графически:
4,8 4,7 5.3 5.2 5.3 4.7 5.0 5.1 4.7 5.0 5.0 4.8 5,1
5,0 4.8 5.2 5.2 5.3 5.0 4.9 5.1 4.9 4.9 5.1 4,8 5,0
4.9 4.9 5.1 4.8 5.2 4.7 5.0 4.8 5.0 4.8 5,0 5,0 5.3
5.0 4.9 5.1 5.1 5.0 5.0 5.1 5.1 5.2 4,9 5,1
Занятие 2. СТАТИСТИЧЕСКИЕ ОЦЕНКИ
ПАРАМЕТРОВ PАСПРЕДЕЛЕНИЯ
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n. Функцию от наблюдаемых случайных значений называют статистической оценкой неизвестного параметра теоретического распределения генеральной совокупности.
Оценкой математического ожидания (выборочной средней) 
называют среднее арифметическое значение признака выборочной совокупности и вычисляют по формулам:
= 
xi/n,
= 
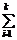xini/n.
Первую формулу применяют, когда все значения признака Х различны или не сгруппированы, а вторую – в случае предварительно сгруппированной выборки, т.е. когда значения Х имеют частоты n1, n2, n3, …, nk.
Несмещенной оценкой дисперсии называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего
S2 = 
(xi - )2/(n - 1) или S2 = 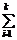(xi - )2ni/(n - 1).
Иногда оценку дисперсии удобнее вычислять по формуле
S2 = (
)/(n - 1).
Оценкой среднего квадратического отклонения называют квадратный корень из оценки дисперсии: s = 
.
Модой Мо называют варианту, имеющую наибольшую частоту. Медианой Ме называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно n = 2k + 1, то Мe=хk + 1; если n = 2k – четное, то Me = (xk + xk + 1)/2.
Размахом вариации R называют разность между наибольшей и наименьшей вариантами R = xmax - xmin.
Коэффициентом вариации V называют отношение выборочного среднего квадратического отклонения к выборочной средней, взятое в процентах:
V = (s / в)´100%.
Эмпирической функцией распределения называют функцию F*(х), которая определяет для каждого значения х относительную частоту события Х < х.
F* (х) = nx/n, где nx - число вариант, меньших х.
Пример 2.1. Для статистического распределения частот, полученного в примере 1.1, вычислить 
, S2, s, Мо, Ме, R, V. Найти функцию F*(х) и изобразить ее графически.
Решение
Распределение было получено в виде:
| xi | Итого | ||||||||
| ni |
Значения признака имеют частоты, т.е. сгруппированы, поэтому вычисления будем производить по соответствующим формулам.
= (37´1 + 38´3 + 39´5 + 40´8 + 41´12 + 42´9 + 43´5 + 44´2)/45 = 40.87.
Для вычисления несмещенной оценки дисперсии используем формулу
S2 = 
(xi - 
)2ni/(n - 1) » 2.66, s » 1.63,
Мо = 41, Ме = (40 + 41)/2 = 40.5,
R = xmax - xmin = 44 - 37 = 7, V = sв / 
в´100% = 1.63/40.87*100% = 3.99%.
Построим эмпирическую функцию F*(х).
Для X < 37, F*(37) = 0, так как значений, меньших 37, не наблюдалось.
Значения X < 38, а именно равное 37, наблюдалось один раз, следовательно, F* (38) = 1/45 = 0.02.
Значения Х < 39, а именно равное 37 и 38, наблюдались 1+3 = 4 раза, следовательно, F* (39) = 3/45 = 0.09.
Значения Х < 40, а именно равное 37, 38 и 39, наблюдались 1+3+5 = 9 раз, следовательно, F*(40) = 9/45 = 0.2.
Значения Х < 41, а именно равное 37, 38, 39 и 40, наблюдались 1+3+5+8 = 17 раз, следовательно, F*(41) = 17/45 = 0.4.
Аналогично F*(42) = 29/45 = 0.6; F*(43) = 38/45 = 0.8; F*(44) = 43/45 = 0.96. Для всех значений Х > 44 очевидно, что F*(х) = 1.
Искомая эмпирическая функция:
F*(х) = 0, для х £ 37;
F*(х) = 0.02, для 37 < х £ 38;
F*(х) = 0.09, для 38 < х £ 39;
F*(х) = 0.2, для 39 < х £ 40;
F*(х) = 0.4, для 40 < х £ 41;
F*(х) = 0.6, для 41 < х £ 42;
F*(х) = 0.8, для 42 < х £ 43;
F*(х) = 0.96, для 43 < х £ 44;
F*(х) = 1.0, для 44 < х.
Построим график функции F*(х)
Задания
2.1. Данные о распределении шести рабочих столярного цеха по уровню квалификации (тарифным разрядам) оказались:
| Порядковые номера рабочих | ||||||
| Тарифные разряды |
Вычислить средний тарифный разряд рабочих.
2.2. Для статистического распределения, полученного в задаче 1.2, вычислить , S2, s, Мо, Ме, R, V. Найти функцию F*(х) и изобразить ее графически.
2.3. Для статистического распределения, полученного в задаче 1.3, вычислить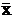 
, S2, s, Мо, Ме, R, V. Найти функцию F*(х) и изобразить ее графически.
Указание. В качестве конкретных значений х берут середины интервалов.
Занятие 3. МЕТОД ПРОИЗВЕДЕНИЙ (МЕТОД
УСЛОВНОГО НУЛЯ). ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ
Если разность между любыми двумя соседними вариантами есть величина постоянная, то говорят о равноотстоящих вариантах, т.е. xk + 1 -
- хk = h – const, h – шаг. В этом случае удобно выборочные среднюю и дисперсию находить методом произведений по формулам
= U' h + C, S2 = (U" - (U')2)h2 n/(n-1),
где U' = 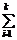Uini/n и U" = 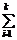U2ini/n, Ui = (xi - C)/h – условные варианты,
i = 1,2,...,k.
С – ложный нуль или новое начало отсчета. В качестве С рекомендуется выбирать варианту, стоящую в середине. В случае четного числа вариант из двух вариант, стоящих в середине, выбирают варианту с наибольшей частотой.
Пример 3.1. Распределение месячной заработной платы 100 строителей задано таблицей:
| Заработная плата (сом) | 500-600 | 600-700 | 700-800 | 800-900 | 900-1000 | 1000-1100 | 1100-1200 |
| Число рабочих |
Вычислить 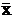, S2, s методом произведений.
Решение
В качестве конкретных значений признака возьмем середины интервалов: х1 = 550, х2 = 650, х3 = 750, х4 = 850, х5 = 950, х6 = 1050, х7 =1150. Имеем случай равноотстоящих вариант с h = 100. Выберем С = 850.
Тогда
U1 = (550 - 850)/100 = -3, U2 = (650 - 850)/100 = -2,
U3 = (750 - 850)/100 = -1, U4 = (850 - 850)/100 = 0,
U5 = (950 - 850)/100 = 1, U6 = (1050 - 850)/100 = 2,
U7 = (1150 - 850)/100 = 3.
Ряд из условных вариант будет иметь вид:
| Ui | -3 | -2 | -1 | Итого | ||||
| ni |
Вычислим
U' = (-3´3 -2´11 -1´20 + 0´30 + 1´19 + 2´12 + 3´5)/100 = 0.07
U" = ((-3)2´3 + (-2) 2´11 + (-1) 2´20 + 12´19 + 22´12 + 32´5)/100 = 2.03
Тогда 
= U' h + C = 0.07´100 + 850 = 857
S2 = (U" - (U')2)h2 n/(n – 1) = (2.03 - (0.07)2)1003 /99 = 20456, s = 143.
Пусть вся совокупность разбита на группы. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю и дисперсию.
Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Если j – номер группы, j = 1,2,…,k, где k – количество групп,
– значения признака в j-й группе,
– частоты признака в j-й группе,
nj - объем j-й группы,
то 
групповые средние, a Sj2 = 
– групповые дисперсии.
Внутригрупповой дисперсией называют среднюю арифметическую групповых дисперсий, взвешенных по объемам групп.
S2внутр = 
.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней.
S2межгр = 
.
Среднюю и дисперсию, вычисленные для всей совокупности, называют общими и обозначают 
и 
.
Справедлива формула = 
+ 
, известная как правило сложения дисперсий.
Пример 3.2. Распределение рабочих строительного треста по стажу работы оказалось следующим:
| UI | Стаж работы, лет | Число рабочих | |||
| СМУ-1 | СМУ-2 | СМУ-3 | Всего | ||
| -2 | 0 – 5 | ||||
| -1 | 5 – 10 | ||||
| 10 – 15 | |||||
| 15 – 20 | |||||
| 20 – 25 | |||||
| 25 – 30 | |||||
| Итого |
Проверить правило сложения дисперсий.
Решение
Конкретные значения признака: х1 = 2,5; х2 = 7,5; х3 = 12,5; х4 = 17,5; х5 = 22,5; х6 = 27,5. Варианты равноотстоящие, с шагом h = 5.
Перейдем к условным вариантам Ui = (хi - C)/h, выбрав С = 12,5. Тогда U1 = -2, U2 = -1, U3 = 0, U4 = 1, U5 = 2, U6 = 3. Запишем их в столбец, левее столбца х. Вся совокупность – строительный трест – разбита на три группы. Вычислим групповые и общие средние и дисперсии методом произведений.
= (-2´1 -1´5 + 1´4 + 2´3 + 3´1)/20 = 0.3 – средняя из условных вариант для 1-й группы,
= (-2´13 -1´5 + 1´3 + 2´3 + 3´2)/30 = -0.53 – средняя из условных вариант для 2-й группы,
= (-2´21 -1´15 + 1´4 + 2´1 + 3´2)/50 = -0.9 – средняя из условных вариант для 3-й группы,
= (-2´35 -1´25 + 1´11 + 2´7 + 3´5)/100 = -0.55 – средняя изусловных вариант для всей совокупности.
" = ((-2)2´1 + (-1) 2´5 + 12´4 + 22´3 + 32´1)/20 = 1.7,
" = ((-2) 2´13 + (-1) 2´5 + 12´3 + 22´3 + 32´2)/30 = 3,
" = ((-2) 2´21 + (-1) 2´15 + 12´4 + 22´1 + 32´2)/50 = 2.5,
" = ((-2) 2´35 + (-1) 2´25 + 12´11 + 22´7 + 32´5)/100 = 2.49.
Вычислим: 
= ´h + C = 0.3´5 + 12.5 = 14;
= ´h + C = -0.53´5 + 12.5 = 9.85;
= ´h + C = -0.9´5 + 12.5 = 8;
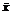общ = ´h + C = -0.55´5 + 12.5 = 9.75.
Вычислим дисперсии по формуле
S2 = (U" - (U')2)h2 n/(n – 1)
S21 = (1.7 - (0.3)2)´52 ´20/19 = 42.37,
S22 = (3 - (-0.53)2)´52 ´20/29 = 70.23,
S23 = (2.5 - (-0.9)2)´52 ´50/49 = 43.11.
Теперь вычислим
S2внутр = (42.37´20 + 70.23´30 + 43.11´50)/100 = 50.67,
S2межгр = ((14 - 9.75)2´20 + (9.85 -9.75)2´30 + (8 - 9.75)2´50)/100 = 5.15,
= 50.67 + 5.15 = 55.82.
Задания
3.1. Для определения крепости нити проведено 1000 испытаний
| Крепость нити, г | 180-190 | 190-200 | 200-210 | 210-220 | 220-230 | 230-240 | 240-250 | Всего |
| Число проб |
Вычислить 
, S2, s методом произведений.
3.2. Распределение сотрудников одной организации по размеру заработной платы оказалось следующим:
| Заработная плата, сом | Число сотрудников | |||
| Отд. 1 | Отд. 2 | Отд. 3 | Всего | |
| 400 -500 | ||||
| 500 - 600 | ||||
| 600 - 700 | ||||
| 700 - 800 | ||||
| 800 - 900 | ||||
| 900 - 1000 | ||||
| 1000 - 1100 | - | - | ||
| Всего |
Проверить правило сложения дисперсий.
Указание: От заданных вариант х, перейти к условным U.
3.3. Результаты хронометража времени, затрачиваемого одним рабочим на изготовление одной детали, приведены в таблице:
| Время, мин | Всего | ||||
| Число рабочих |
Определить среднее время, затрачиваемое одним рабочим на изготовление одной детали.
3.4. Распределение рабочих мебельной фабрики по уровню квалификации было следующим:
| Тарифные разряды | Количество рабочих | |||
| Цех 1 | Цех 2 | Цех 3 | Всего | |
| Всего |
Проверить правило сложения дисперсий.
Занятие 4. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ
ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
И СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ, РАСПРЕДЕЛЕННОЙ
ПО НОРМАЛЬНОМУ ЗАКОНУ
Статистическую оценку, определяемую одним числом, называют точечной.
Статистическую оценку, определяемую двумя числами - концами интервала, покрывающего оцениваемый параметр, называют интервальной.
Пусть q* – статистическая оценка для оцениваемого параметра q. Оценка q* тем точнее оценивает параметр q, чем меньше разность |q - q*|. Если |q - q*| < d, d > 0, то чем меньше d, тем точнее оценка q*. Положительное число d называют точностью оценки. Найти точность оценки можно только с заданной вероятностью.
Надежностью (доверительной вероятностью) оценки q по q* называют вероятность g, с которой осуществляется неравенство
|q - q*| < d, d > 0, т. е. Р(|q - q*| < d) = g.
Надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Чаще всего задают надежность, равную 0.9; 0.95; 0.99.
Интервал (q* - d; q* + d), который покрывает неизвестный параметр q с заданной надежностью g, называют доверительным.
Доверительный интервал и есть интервальная оценка.
Математическое ожидание М(x) = m нормально распределенной величины Х оценивается по выборочной средней . Доверительный интервал при известном среднем квадратическом отклонении s имеет вид
- z´s/ 
< m < 
+ z´s/ 
,
где n – объем выборки, z – параметр.
Параметр z определяется из условия F(z) = g/2, где F(z) – функция Лапласа. Значения этой функции берут из таблиц (см. Приложение 1). Величина z´s/ = d – точность оценки. При неизвестном среднем квадратическом отклонении его значение заменяется оценкой по выборке и доверительный интервал для математического ожидания принимает вид:
- tg´S/ < m < + tg´S/ ,
s – несмещенное выборочное среднее квадратическое отклонение, вычисляемое по формуле
s = 
,
tg(n) – параметр, значения которого берут из специальных таблиц (см. Приложение 2) в зависимости от объема выборки n и надежности g. Число степеней свободы n определяется как объем выборки минус количество параметров, определенных по выборке, n = n – k, где k – количество параметров, определенных по выборке.
Среднее квадратичеcкое отклонение s(x) нормально распределенной случайной величины оценивают по несмещенному выборочному среднему квадратическому отклонению. Доверительный интервал для s имеет вид
s´(1 - q) < s < s´(1 + q),
q – параметр, значения которого зависят от объема выборки n и надежности g и берут из таблиц (см. Приложение 3).
Пример 4.1. Найти доверительный интервал для неизвестного математического ожидания нормально распределенного признака с надежностью g = 0,99, если известно генеральное среднее квадратическое отклонение s = 3 и по данным выборки n = 25 вычислена = 20.12.
Решение
Доверительный интервал ищем в виде - zg´s/ 
< m < + zg´s/ . Найдем параметр z из условия F(z) = 0.99, а с учетом того, что критическая область двухсторонняя – 0.995.
По таблице (Приложение 1) находим zg = 2.58.
Доверительный интервал
20.12 - 2.58´3/ 
< m < 20.12 + 2.58´3/ 
8.57 < m < 21.67.
Пример 4.2. Найти доверительный интервал с надежностью g = 0.95 для М(х) = m нормально распределенного признака, если по данным выборки объема n = 12 вычислены выборочная средняя =16.8 и несмещенное выборочное среднее квадратическое отклонение s = 1,5.
Решение
Доверительный интервал ищем в виде
- tg´s/ < m < + tg´s/ .
Параметр tg = tg(12 - 1, 0.975) найдем по таблице (Приложение 2). tg = 2.20.
Тогда
6.8 - 2.2´1.5/ 
< m < 16.8 + 2.2´1.5/ ,
5.85 < m < 17.75.
Пример 4.3. Найти с надежностью 0.99 доверительный интервал для s нормально распределенного признака, если по данным выборки объема n = 16 вычислено s = 0.400.
Решение
Доверительный интервал ищем в виде
s´(1 - q) < s < s´(1 + q)
Из таблицы (Приложение 3) находим q = q(16; 0,.99), q = 1.07, тогда 0 < q < 0.400(1 +1.07), 0 < q < 0.828.
Задания
4.1. Рост призывников нормальная случайная величина со средним квадратическим отклонением s = 5.92. Определить, в каких доверительных границах с вероятностью 0.95 находится рост призывников в генеральной совокупности, если по данным выборки объема n = 1000 вычислено = 168.
4.2. По данным 16 независимых равноточных измерений некоторой физической величины найдены выборочная средняя = 42.8 и несмещенное выборочное среднее квадратичное отклонение s = 8. Оценить с надежностью 0.99 истинное значение измеряемой величины.
4.5. Выборочное обследование величины вклада в одном из банков по 100 лицевым счетам дало следующие результаты:
| Интервалы вклада, $ | 0-50 | 50-100 | 100-500 | 500-1000 | 1000-1500 | 1500-2000 | 2000-5000 |
| Число счетов |
Определить с доверительной вероятностью 0.99 возможные пределы для средней величины вклада в данном банке.
4.4. Найти минимальный объем выборки, при котором с надежностью 0.925 точность оценки математического ожидания нормально распределенного признака по выборочной средней будет равна 0.2, если известно s = 1.5.
4.5. Произведено 10 измерений одним прибором некоторой физической величины, причем исправленное среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0.8. Найти точность прибора с надежностью 0.95. Точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
4.6. Испытание крепости отобранных 150 нитей дало следующие результаты:
| Крепость нити, г | 210-250 | 250-290 | 290-330 | 330-370 |
| Число проб |
Определить с надежностью 0.99 среднюю крепость нитей всей партии, считая ее нормальной случайной величиной.
4.7. Для определения точности измерительного прибора было проведено 10 независимых измерений, на основании которых вычислена несмещенная выборочная дисперсия S2 = 4 мм2. Найти с точностью 0.95 доверительный интервал точности этого измерительного прибора.
Занятие 5. КРИТЕРИЙ СОГЛАСИЯ c2
Пусть относительно интересующей случайной величины Х проведено выборочное наблюдение, давшее результаты:
| x1 | x2 | … | xk |
| n1 | n2 | … | nk |
На предыдущих занятиях были рассмотрены вопросы оценки неизвестных параметров этой величины. Если неизвестен и закон распределения этой величины, но имеются основания предположить, что он имеет определенный вид (назовем А), то выдвигают гипотезу: генеральная совокупность распределена по закону А.
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Для статистической проверки гипотезы о том, что выборочная совокупность (выборка) имеет предполагаемый закон распределения, применяются различные критерии согласия. Критерием согласия (это специально подобранная случайная величина) называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Рассмотрим критерий согласия c2 (читается хи-квадрат) или критерий Пирсона, названный так по имени автора, впервые предложившего его. Сравнивают эмпирические (наблюденные) и теоретические (вычисленные в предположении о данном законе распределения) частоты.
c2 = 
,
где foi – наблюдаемая частота для каждой группы i;
fti – теоретическая частота для каждой группы.
Если вычисленное значение критерия равно нулю, то наблюдаемые и теоретические предполагаемые значения частот точно совпадают и распределение выборочной совокупности считается точно совпадающим с предполагаемым нами распределением. Если значение критерия не равно нулю, расхождение существует и проверка значимости расхождения (со статистической точки зрения) проводится по таблицам для выбранного (заданного) уровня значимости a (в некоторой литературе приведена обратная величина – уровень доверительной вероятности (1 – a) и имеющегося числа степеней свободы. Таблицы критерия c2 приведены в Приложении 4.
Основные правила применения критерия Пирсона:
1. Объем выборочной совокупности должен быть не менее 100, в противном случае необходимо применять другие критерии, например, Колмогорова-Смирнова или Крамера-фон Мизеса;
2. Группы необходимо составлять таким образом, чтобы в каждой из них частота (как наблюдаемая, так и теоретическая) была не менее 5. Если в группе какая-либо из частот менее 5, то необходимо ее объединять с предшествующей группой. Правила составления групп в общем случае произвольные, но некоторые приемы можно конкретизировать.
Для дискретных распределений понятие группы совпадает с фиксированным значением аргумента.
Для непрерывных распределений проще всего разбить теоретическую функцию плотности предполагаемого распределения на одинаковые по площади участки, границы этих участков и будут границами групп. Теоретическая частота в этом случае будет постоянной для всех групп и равна площади одного участка под теоретической функцией распределения, умноженной на объем выборки. Наблюдаемая частота для каждой группы определяется как количество элементов выборки, попавших в границы конкретного участка. Если непрерывное распределение задано выборкой небольшого числа сгруппированных значений, то можно принять границы участков в середине между каждыми значениями. Левой границей первого участка в этом случае будет -¥, а правой границей последнего участка +¥;
3. Число степеней свободы определяется по формуле m = k – p – 1, где k – количество групп после проведения операций объединения, если они оказались необходимы, p – количество параметров, определенных по выборке для построения теоретических частот. В каждом конкретном случае это число различно и определяется видом предполагаемого распределения, с которым мы хотели бы провести сравнение. Например, для распределения Пуассона р = 1, а для нормального распределения р = 2.
Пример 5.1. По результатам наблюдения работы АТС были получены следующие данные о частоте звонков за одноминутный интервал
| Число запросов, х | ||||||
| Число одноминутных интервалов с х запросами |
Требуется проверить, имеет ли эта выборка распределение Пуассона. Уровень значимости принять равным 0.05.
Решение
Общее число одноминутных интервалов равно 509. Распределение