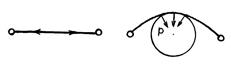
Представим себе растянутую резиновую полоску, поперечный разрез которой показан на рис. 72, а.
а б
Р и с. 72
Пока она сохраняет плоскую форму, в ней действуют только силы натяжения, направленные в ее плоскости. Сообщим резиновой полоске искривленную форму надавливанием ею на поверхность твердого шара (рис. 72, б). Стремясь выпрямиться, полоска резины оказывает на шар давление по нормали к своей поверхности. Это давление направлено в ту сторону, куда обращена вогнутая сторона полоски резины.
Совершенно такое же явление происходит на поверхности жидкости. Если ее поверхность плоская, то силы поверхностного натяжения лежат в этой плоскости и не имеют составляющей, перпендикулярной поверхности жидкости. Жидкость с плоской поверхностью, таким образом, находится, как мы это выяснили ранее, только под молекулярным давлением p Μ. Если же поверхность жидкости искривлена, как, например, в шарообразной капле (рис. 73, а), то к p Μ прибавляется то добавочное (избыточное) давление p Л, которое вызвано кривизной поверхности, так что полное давление p на поверхности жидкости можно представить в виде суммы двух давлений:
где p Л – избыточное давление, которое называют давлением Лапласа.
Сила избыточного давления Лапласа направлена к центру кривизны поверхности жидкости. В самом деле, возьмем на сферической капле (рис. 73, а) контур в виде окружности.
а б в
Р и с. 73
На каждый элемент этого контура действует сила поверхностного натяжения, направленная по касательной к капле. Равнодействующая этих сил направлена к центру капли, а разделенная на площадь, ограниченную контуром, даст давление Лапласа, которое при выпуклой поверхности жидкости добавляется к молекулярному давлению p Μ.
Если же поверхность жидкости вогнутая, как в пузырьке в жидкости, то равнодействующая сил поверхностного натяжения будет направлена к центру пузырька и будет уменьшать давление, под которым находится жидкость:
p = p Μ– p Л
Вычислим величину этого добавочного давления p Л. Рассмотрим сначала частный случай, когда жидкость ограничена боковой поверхностью прямого круглого цилиндра (рис. 73, б). На поверхности цилиндра выберем бесконечно узкую площадку длины b. Дуга АВ окружности стягивается бесконечно малым углом d j. На боковые стороны площадки действуют силы поверхностного натяжения b s.
Равнодействующая этих сил направлена, очевидно, по радиусу СО цилиндра и равна (рис. 73, б,в).
(5.4.1)
где a – длина дуги АВ, a dS = ab – площадь бесконечно узкой площадки, заштрихованной на рис. 73, б. Разделив силу FP на площадь dS, найдем избыточное давление Лапласа:
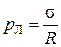. (5.4.2)
Обобщим формулу (5.4.2) на случай, когда жидкость ограничена поверхностью двойной кривизны (рис. 74).
Р и с. 74
Для этого рассмотрим на поверхности жидкости бесконечно малую площадку АВCD площади dS. Пусть эта площадка в направлении АD имеет радиус кривизны R 1, а в направлении АВ (перпендикулярном АD) – R 2. Поверхность АВCD можно рассматривать как часть поверхности цилиндра радиуса R 1и длины АВ, на противоположные стороны АВ и CD которой действуют касательные силы поверхностного натяжения, результирующая которых, очевидно, нормальна к поверхности жидкости и, согласно (5.4.1), равна
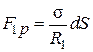. (5.4.3)
С другой стороны, ту же поверхность АВCD можно рассматривать как часть поверхности другого цилиндра радиуса R 2 и длины АD, на противоположные стороны AD и BC которого действуют касательные силы поверхностного натяжения, результирующая их также нормальна к поверхности жидкости и равна
. (5.4.4)
Так как силы F 1 p и F 2 p параллельны, то суммарная сила поверхностного натяжения, действующая на прямоугольник АВCD,
. (5.4.5)
Разделив эту сумму на площадь прямоугольника АВCD, получим формулу для избыточного давления Лапласа:
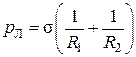. (5.4.6)
В дифференциальной геометрии доказывается, что сумма обратных радиусов кривизны для любой пары взаимно перпендикулярных (нормальных) сечений, проведенных через данную точку поверхности, имеет одно и то же значение независимо, где эта точка взята на поверхности. (Нормальным сечением поверхности в некоторой точке называется линия пересечения этой поверхности с плоскостью, проходящей через нормаль к поверхности в рассматриваемой точке.) Радиус кривизны считается положительным, если соответствующее нормальное сечение вогнуто в сторону жидкости. В противном случае оно отрицательно.
Таким образом, формула Лапласа (5.4.6) дает общее выражение для избыточного давления для любых поверхностей, ограничивающих жидкость.
Рассмотрим частные случаи формулы Лапласа.
1. Жидкость ограничена сферической поверхностью радиуса R. В этом случае радиусы кривизны нормальных сечений в любой точке сферы одинаковы R 1 = R 2 = R и давление Лапласа
. (5.4.7)
2. Жидкость ограничена боковой поверхностью прямого кругового цилиндра радиуса R. Тогда, R 1 = R, R 2 = ¥и
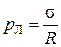. (5.4.8)
Жидкость ограничена плоской поверхностью. В этом случае
R 1 = R 2 = ¥, p Л = 0.
Пример 1. Выясним, какой должна быть разность давлений воздуха внутри и вне мыльного пузыря, чтобы он находился в равновесии (не увеличивался и не уменьшался его радиус) (рис. 75).
а б
Р и с. 75 Р и с. 76
Для равновесия шарообразного мыльного пузыря необходимо, чтобы сумма внешнего давления p 0, молекулярного давления p Ми давления Лапласа на внешней (выпуклой) поверхности 
равнялось сумме давления p воздуха (и паров жидкости) внутри пузыря, молекулярного давления p Μи давления Лапласа на внутренней (вогнутой) поверхности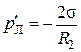 
, т. е.
Откуда искомая разность давлений
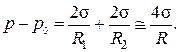
Ввиду малой толщины мыльной пленки положено R 1 @ R 2 = R.
Капиллярные явления
Поместим цилиндрическую трубку малого сечения (капилляр) одним концом в жидкость, налитую в широкий сосуд (рис. 76).
Если жидкость частично смачивает капилляр, то ее поверхность в капилляре будет вогнутой сферической формы (рис. 76, а). При этом жидкость в капилляре поднимется на некоторую высоту h. Это можно объяснить тем, что давление на плоской поверхности жидкости, равное сумме атмосферного давления p 0и молекулярного давления p Мбольше, чем давление p 0 +p М–2s /R на вогнутой поверхности мениска на величину давления Лапласа. Вследствие этой разности давлений жидкость в капилляре поднимется до такого уровня h, при котором гидростатическое давление столба жидкости r gh уравновесится давлением Лапласа p Л = 2s /R, где R – радиус сферы мениска, т. е.
.
Откуда
. (5.5.1)
Как видно из рис. 76 радиус кривизны мениска R связан с радиусом капилляра r равенством R = r/ cosq, где q – краевой угол. Учтя это, перепишем (5.5.1) в виде
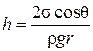. (5.5.2)
Если жидкость полностью смачивает твердое тело капилляра (к примеру, вода - чистое стекло), то q = 0и
. (5.5.3)
В этом случае сферическая поверхность мениска вписана во внутреннюю поверхность цилиндрического капилляра (R = r).
Если же жидкость частично не смачивает капилляр (рис.76, б), то давление на плоской поверхности жидкости, равное p 0 + p М, будет меньше, чем давление p 0 +p М = 2s /R на выпуклой поверхности мениска, в результате чего жидкость в капилляре опустится на величину h, определяемую формулой (5.5.2). При этом h < 0, так как при частичном несмачивании краевой угол p2 £ q £ pи cosq <0.