Если при частоте w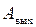 
будет больше, чем 
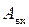, то в замкнутой системе при этой частоте возникнут нарастающие колебания. Если же 
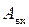будет меньше, чем , то колебания в замкнутой системе будут затухающие.
Поведение амплитуды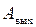 
при изменяющейся частоте w удобно наблюдать с помощью годографа передаточного коэффициента или с помощью так называемого годографа Михайлова.
Исследование устойчивости системы по виду годографа передаточного коэффициента
Рассмотрим дифференциальное уравнение
.
При гармоническом возмущении системы изменение величины у имеет синусоидальный характер:
.
Синусоидальные величины можно представить также в комплексном виде. При этом такой вид будет являться изображением вышеприведённого оригинала. Использование комплексного вида облегчает многие операции с синусоидальными величинами.
Приведённой зависимости в комплексном виде соответствует зависимость
.
Пример геометрического изображения синусоидальной величины на плоскости комплексных чисел представлен на рисунке.
Объясняется это следующим образом.
Синусоидальную функцию можно изобразить проекцией вращающегося в декартовой плоскости координат радиус-вектора на одну из осей.
Здесь A – амплитуда колебаний, а y – их начальная фаза. Причём синусом является проекция вектора с углом поворота y или 
на ось ординат, а косинусом – на ось абсцисс.
Такой вид изображения колебаний удобен при суммировании колебаний с разными амплитудами и начальными фазами. С его помощью легко найти амплитуду и начальную фазу результирующих колебаний[1]:
,
где
,
.
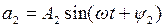Параметры A и y для 
можно найти, пользуясь тригонометрическим преобразованием:
.
(Если речь идёт о проекции вращающихся векторов на ось абсцисс, то есть о косинусе функций, то используют преобразование
.)
Тогда,
,
,
.
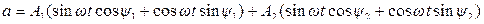Из последнего уравнения очевидно, что
,
.
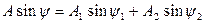Следовательно,
,
,
[2].
Однако такой подход не очень удобен, особенно, если суммируется больше двух колебаний. Поэтому для решения этой задачи обычно прибегают к чисто геометрическим построениям, жертвуя точностью результата.
Возможность проведения точных аналитических расчётов дает перенос радиус-вектора, изображающего синусоидальную функцию времени, на плоскость комплексных чисел.
Всякая действительная функция 
, имеющая на интервале 
n -ю производную 
может быть разложена в ряд Тейлора следующим образом:
,
где 
называется остаточным членом формулы Тейлора.
Раскладывая в ряды различные функции, можно заметить схожесть между разложением в ряд функций 
, 
, а также функции 
. Приведём эти ряды:
,
,
Из приведённых формул видно, что сумма разложений в ряд и отличается от разложения в ряд только знаками. В самом деле,
В XVIII веке, когда жил Эйлер, уже было известно число 
. Им пользовались ещё итальянские математики эпохи возрождения при решении алгебраических уравнений определённого типа. Воспользовавшись тем, что 
, 
, 
и т. д., Эйлер при разложении в ряд заменил аргумент z функции на 
:
На основании последнего выражения он сделал вывод, что
.
Эта формула (которая называется формулой Эйлера) лежит в основе всех комплексных чисел.
Заменим ось Ox на ось действительных чисел Re (от фр. reel – действительный, лат. realis), а ось Oy на ось мнимых чисел Im (от фр. imaginaire – мнимый, лат. imaginari(u)s), сохранив все условия изображения (рис. 6, 7).
 |  |
Такое изображение соответствует геометрическому изображению модуля комплексного числа радиус-вектором.
Запишем комплексное число, пользуясь нашими обозначениями:
.
Тогда модулем числа A будет являться величина
.
Запись комплексного числа можно представить в тригонометрической форме:
.
Пользуясь формулой Эйлера 
, можно перейти к показательной форме:
.
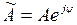Таким же образом можно записать колебания в любой момент времени t:
,
.
Обратим внимание, что мнимая часть комплексного числа равна величине а в обычной форме записи синусоидальных колебаний:
.
Поэтому всегда легко осуществить переход от комплексной формы записи к обычной. Для этого достаточно выделить мнимую часть.
Итак, в приведённом дифференциальном уравнении выходная величина у меняется по синусоидальному закону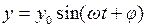 
, которому в комплексном виде соответствует закон 
(или 
, и 
).
Пусть на вход подается сигнал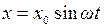 
. Этому сигналу в комплексной форме соответствует 
(или 
, и 
).
Отношение 
называется передаточным коэффициентом.
.
Здесь 
– модуль передаточного коэффициента.
Представим 
в тригонометрической форме:
.
Введём обозначения: 
и 
. Соответственно 
.
Тогда в алгебраической форме будет иметь вид:
.
Графическое изображение модуля передаточного коэффициента представлено на рисунке.
Как известно, при частотном методе анализа динамических звеньев частоту w предполагают переменной величиной. Но при изменении частоты w будет меняться и амплитуда колебаний на выходе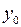 
, а следовательно, и величина 
, а также передаточный коэффициент .
Таким образом, при переменной частоте w радиус-вектор 
становится переменным (он меняется по модулю 
и углу j) и описывает своим концом некоторую кривую, называемую годографом.
(Годограф вектор-функции – кривая, представляющая собой множество концов переменного вектора, начало которого для всех t есть произвольная фиксированная точка).
Годограф передаточного коэффициента можно построить, пользуясь аналитическими расчётами (для этого надо знать все характеристики динамического звена), а можно построить по результатам эксперимента.
Рассмотрим первый способ.
Наше уравнение
можно записать в комплексном виде следующим образом.
Поскольку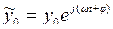 
, то
,
и т. д.
Поэтому (с учётом того, что в правой части уравнения стоит ) запишем:
Тогда
Чтобы построить годограф передаточного коэффициента, надо при каждом значении w откладывать по горизонтальной оси действительную часть P, а по вертикальной оси мнимую часть Q.
Для этого, прежде всего, надо избавиться от мнимой единицы в знаменателе.
Если представить знаменатель функции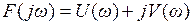 
, то
Чтобы избавиться от j в знаменателе, надо и числитель и знаменатель умножить на 
.
Получим
.
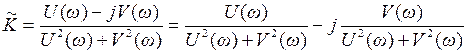Здесь 
, 
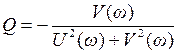
Поскольку 
, , то для того, чтобы найти 
, надо сложить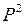 
и 
и извлечь квадратный корень:
.
Поскольку , то
.
Годограф 
обычно называют амплитудно-фазовой характеристикой.
Критерий устойчивости будет следующим.
Если амплитудно-фазовая характеристика разомкнутой системы, построенная для всех значений частоты от 0 до ¥, не охватывает точку (-1; j 0), то система в замкнутом состоянии будет устойчива, если же амплитудно-фазовая характеристика охватывает эту точку, то система в замкнутом состоянии будет неустойчива.
 | |
Если амплитудно-фазовая характеристика проходит через точку (-1; j 0), это означает равенство амплитуд входного и выходного воздействия и отсутствие сдвига фаз между ним. В этом случае система находится на границе устойчивости.
Если аналитически не удаётся рассчитать и построить амплитудно-фазовую характеристику, то её можно построить по результатам эксперимента.
Для этого систему возмущают по гармоническому закону с определенной амплитудой и частотой, изменяемой с определенным шагом.
После того, как на каждом шаге колебания установятся, измеряют амплитуду на выходе и разность фаз между выходом и входом.
При построении радиус-вектора, его длиной служит отношение амплитуды на выходе к амплитуде на входе.
Исследование устойчивости системы по критерию Михайлова
Критерий Михайлова дает необходимое и достаточное условие асимптотической устойчивости линейного дифференциального уравнения n -го порядка
.
Если переписать это уравнение в виде:
,
,
то получим полином ,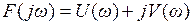
где
,
.
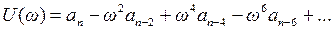Поскольку дифференциальному уравнению соответствует полином
,
то критерий Михайлова звучит так: все корни многочлена
с действительными коэффициентами имеют строго отрицательные действительные части тогда и только тогда, когда комплекснозначная функция 
действительного переменного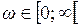 
описывает в комплексной плоскости р кривую (годограф Михайлова), начинающуюся на положительной действительной полуоси, не попадающую в начало координат и последовательно проходящую против хода часовой стрелки n квадрантов.
Эквивалентное условие: когда радиус-вектор 
при возрастании w от 0 до +¥ нигде не обращается в нуль и монотонно поворачивается в положительном направлении на угол 
.
| |
При построении годографа Михайлова по горизонтальной оси откладываются значения 
, а по вертикальной 
.
Если известен вид дифференциального уравнения, описывающего работу звена, и его коэффициенты, то определение данных для построения годографа представляется более простым, чем в случае оценки по передаточному коэффициенту.
Но построить годограф Михайлова можно и по экспериментальным данным, хотя это потребует некоторых дополнительных расчётов.
В результате эксперимента, как известно, мы при каждом значении возмущающей частоты имеем значение амплитуды на выходе, а также разность фаз колебаний между входом и выходом j.
Амплитуда на входе при этом постоянна. Отношение амплитуды на выходе к амплитуде на входе обозначим К.
Пользуясь вышеприведенными обозначениями, определим величины 
и 
для построения годографа Михайлова.
Выпишем некоторые зависимости, выведенные нами для годографа передаточного коэффициента.
; ; ;
;
; ;
.
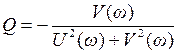Поскольку 
, то
,
,
откуда
,
,
.
(Здесь использована зависимость 
).
Таким образом, частотный метод анализа устойчивости динамических звеньев имеет следующие преимущества:
1) метод может быть применён к системам, уравнения звеньев которых неизвестны. Метод Рауса-Гурвица в этом случае неприменим, а для частотного метода достаточно снять амплитудно-фазовую характеристику экспериментально;
2) метод позволяет оценить влияние отдельных звеньев на устойчивость системы, поскольку передаточный коэффициент системы равен произведению передаточных коэффициентов отдельных её звеньев, а фаза системы – сумме фаз отдельных звеньев;
3) метод может быть применён с некоторыми изменениями для систем с нелинейными звеньями.
Список рекомендуемой литературы
Основная литература
1. Власов, В. М. Информационные технологии на автомобильном транспорте / В. М. Власов, А. Б. Николаев, А. В. Постолит, В. М. Приходько; под общ. ред. В. М. Приходько; МАДИ (Гос. техн. ун-т). – М.: Наука, 2006. – 283 с.
2. Волков, В. С. Электроника и электрооборудование транспортных и транспортно-технологических машин и оборудования: Учебник. 2-е изд., перераб. и доп. – М.: ИЦ «Академия», 2013. – 368 с.
3. Гетманенко, В. М. Современные электронные устройства автотранспортных средств: учеб. пособие. – Зерноград: Изд. ФГОУ ВПО АЧГАА, 2008. – 149 с.
4. Иванов, А. М. Автомобили. Теория эксплуатационных свойств: учебник. / А. М. Иванов, А. Н. Нарбут, А. С. Паршин, А. Н. Солнцев, В. В. Гаев-ский; под ред. А. М. Иванова. – М.: Академия, 2013. – 176 с.
5. Коновалов, Б. И. Теория автоматического управления. / Б. И. Коновалов, Ю. М. Лебедев. – СПб.: Лань, 2010. – 224 с.
6. Пржибыл, П. Телематика на транспорте. / П. Пржибыл, М. Свитек; под ред. В. В. Сильянова. – М: МАДИ (ГТУ), 2003. – 540 с.
7. Ревин, А. А. Автоматика и автоматизация производственных процессов на автомобильном транспорте: учебное пособие / А. А. Ревин, В. С. Котов. – Волгоград: ИПК «Царицын», 1993. – 96 с.
8. Решедько, В. В. Электроника и электрооборудование транспортных и транспортно-технологических машин: учеб. пособие. – Новосибирск: Изд-во СГУПСа, 2009. – 227 с.
9. Ютт, В. Е. Эксплуатация антиблокировочных систем грузовых автомобилей: Учебное пособие. / В. Е. Ютт, А. М. Резник, В. В. Морозов, А. И. Попов. – М.: Горячая линия – Телеком, 2010. – 88 с.
10. Ютт, В. Е. Эксплуатация электронных систем автомобилей: учеб. пособие. / В. Е. Ютт, А. М. Резник, В. В. Морозов, А. И. Попов. – М.: Изд. МАДИ, 2012. – 253 с.
11. Ютт, В. Е. Электронные системы управления ДВС и методы их диагностирования: учеб. пособие / В. Е. Ютт, Г. Е. Рузавин. – М.: Горячая линия – Телеком, 2007. – 104 с.
Дополнительная литература
12. Камке, Э. Справочник по обыкновенным дифференциальным уравнениям / Э. Камке. – СПб: Лань, 2011. – 336 с.
13. Ляпунов, А. М. Общая задача об устойчивости движения / А. М. Ляпунов. – М., Л.: Государственное издательство технико-теоретической литературы, 1950. – 473 с.
14. Максвелл, Д. К. Теория автоматического регулирования (Линеаризованные задачи) / Д. К. Максвелл, И. А. Вышнеградский, А. Стодола; под ред. А. А. Андронова и И. Н. Вознесенского. – М.: Изд-во Академии наук СССР, 1949. – 431 с.
15. Ревин, А. А. Теория эксплуатационных свойств автомобилей и автопоездов с АБС в режиме торможения. / А. А. Ревин. – Волгоград: Изд-во ВолгГТУ, 2002. – 372 с.
16. Соглашение о принятии единообразных технических предписаний для колесных транспортных средств, предметов оборудования и частей, которые могут быть установлены и/или использованы на колёсных транспортных средствах, и об условиях взаимного признания официальных утверждений, выдаваемых на основе этих предписаний. Единообразные предписания, касающиеся официального утверждения транспортных средств категорий M, N и О в отношении торможения. Правила № 13 пересмотр 4 ЕЭК ООН. 2000 г. – 180 с.
17. Стручалин, В. М. Техническая эксплуатация автомобилей, оборудованных компьютерными системами: учеб. пособие / В. М. Стручалин. – Краснодар: Изд-во КубГТУ, 2009. – 194 с.
18. Соснин, Д. А. Новейшие автомобильные электронные системы / Д. А. Соснин, Д. С. Яковлев. – М.: СОЛОН – Пресс, 2005. – 240 с.
19. Чебышёв, П. Л. Избранные труды / П. Л. Чебышёв. – М.: Изд-во Академии наук СССР, 1955. – 929 с.
20. Эйдинов, А. А. Автотранспортные средства с комбинированными энергоустановками (АТС и КЭУ): учеб. пособие / А. А. Эйдинов, В. Е. Ютт, В. Ф. Кутенёв, И. М. Минкин, К. М. Сидоров. – М.: Изд-во МАДИ, 2010. – 155 с.
Оглавление
Задание к контрольной работе......................... 3
Варианты заданий................................ 5
Методические указания по выполнению контрольной работы....... 20
Составитель Константин Владимирович Чернышов
АВТОМАТИКА И АВТОМАТИЗАЦИЯ НА ТРАНСПОРТЕ
Задания и методические рекомендации по выполнению контрольной работы
Темплан 2017 г. Поз. № 112
Подписано в печать 05.11.2017. Формат 60´84 1/16.
Бумага газетная. Печать офсетная. Усл. печ. л. 3,25.
Гарнитура Times. Тираж 100 экз. Заказ.
Волгоградский государственный технический университет.
400131 Волгоград, просп. им. В. И. Ленина, 28.
РПК “Политехник”
Волгоградского государственного технического университета.
400131 Волгоград, ул. Советская, 35.
|
[1] Заметим, что частота и время в расчётах не участвуют.
[2] Последними формулами подтверждается сноска на предыдущей странице.