Вариант A
Задание 1.
Найти 
и 
.
Решение. Находим
,
.
Задание 2.
Найти 
, если:
а) 
; б) 
.
Решение. а) Находим
.
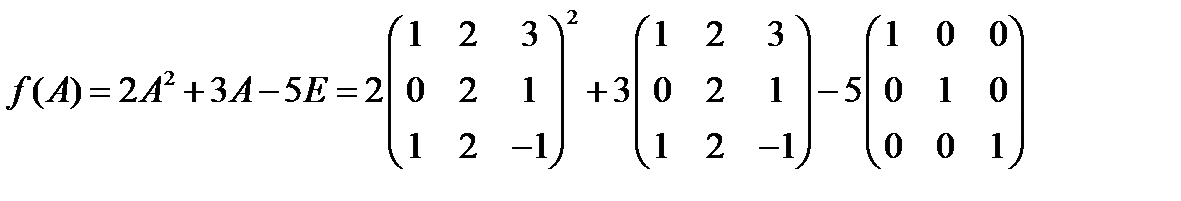Поскольку
,
то
.
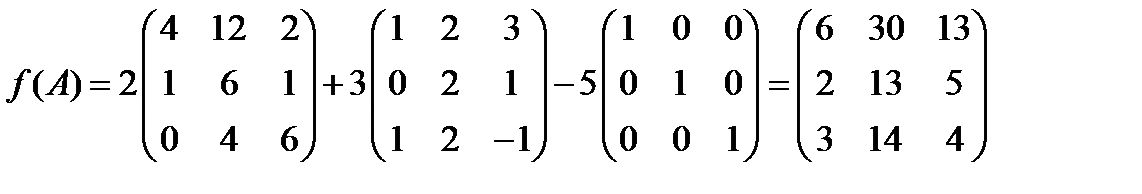б) Находим
.
Поскольку
,
то
.
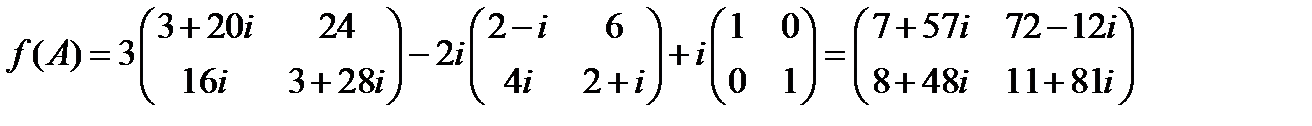Задание 3.
Специальные виды матриц:
а) Найти все матрицы второго порядка, перестановочные с матрицей 
.
б) Вычислить 
и 
, если 
.
Решение. а) Пусть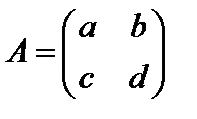 
, тогда должно выполняться равенство
.
После умножения получаем
,
Записывая равенство соответствующих элементов этих матриц, получаем систему уравнений
Следовательно, искомые матрицы имеют вид
.
Например, пусть 
, тогда
.
Действительно,
.
б) Выписываем эрмитово сопряженную матрицу
.
Тогда
,
.
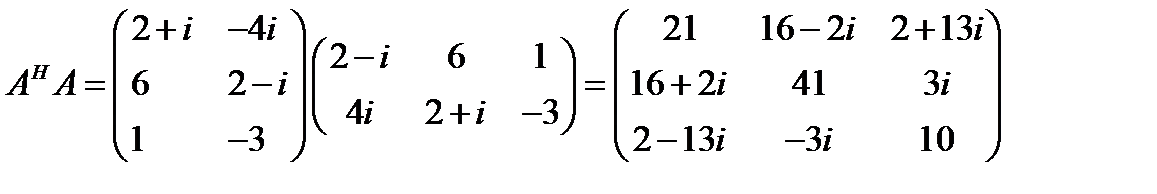Заметим, что обе матрицы будут эрмитовы.
Задание 4.
Блочные матрицы. Найти AB, а) учитывая разбиение на блоки; б) без учета разбиения на блоки, если:
.
Решение. В данном случае можно написать
,
где
,
,
,
.
В результате получаем следующую блочную матрицу
.
Перемножим матрицы без учета разбиения на блоки:
.
Задание 5.
Привести матрицу A: а) к упрощенному виду при помощи преобразований строк; б) к простейшему виду. Последовательность преобразований записать при помощи умножения элементарных матриц и преобразующих элементарных матриц.
.
Решение. При помощи элементарных преобразований строк приводим матрицу к упрощенному виду:
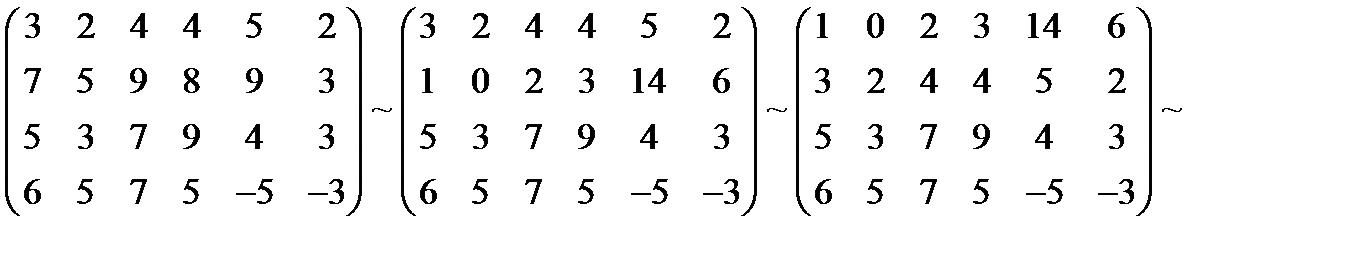
Умножив вторую строчку на (–1), мы получаем матрицу упрощенного вида
.
Результаты преобразований можно записать в матричном виде следующим образом:
,
где
Приведем теперь матрицу 
к простейшему виду при помощи преобразования столбцов:
.
Меняя местами 3-ю и 4-ю столбцы местами, получим матрицу простейшего вида.
Результаты преобразований можно записать в матричном виде следующим образом:
|
|
,
где
Задание 6.
Вычислить определители:
а)  ;
| б)  ;
| в)  ;
| |
г)  ;
| д)  .
| ||
Решение. а) Преобразуем определитель и вычисляем
.
б) Расписываем определитель по правилу треугольников или Саррюса, получаем
.
в) При помощи элементарных преобразований приводим определитель к треугольному виду:
г) При помощи элементарных преобразований приводим определитель к треугольному виду:
.
д) При помощи элементарных преобразований приводим определитель к треугольному виду:
.
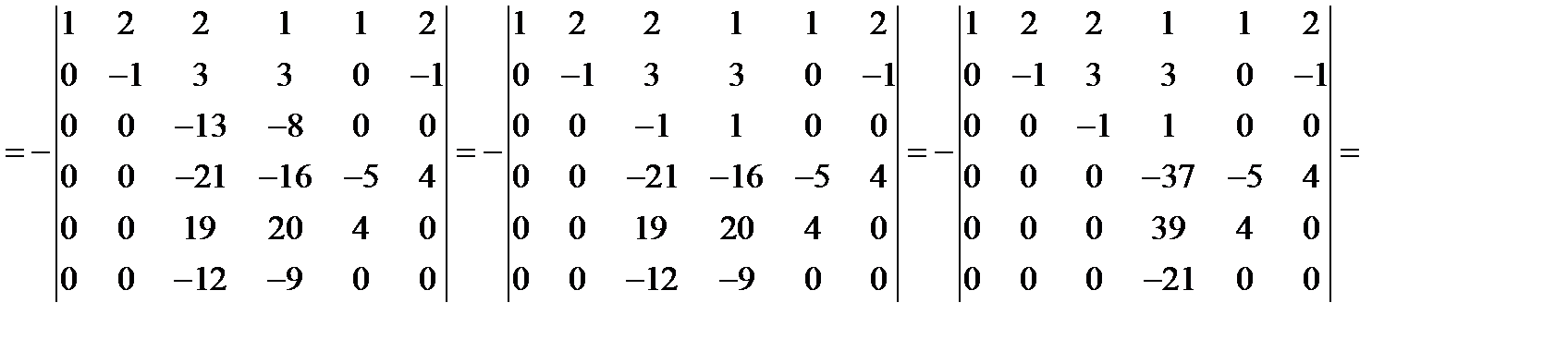
Задание 7.
Вычислить определители n -го порядка:
а)  ;
| б)  .
|
Решение. а) От последнего столбца отнимем предпоследний и т.д.:
.
б) Разложим определитель по первой строке:
.
В результате получаем рекуррентное уравнение
.
Составим характеристическое уравнение:
.
Это уравнение имеет один корень кратности 2: 
. Поэтому решение будем искать в виде
,
где С 1 и С 2 – неизвестные коэффициенты. Подберем теперь коэффициенты С 1 и С 2 так, чтобы при 
и 
она давала правильные результаты, т.е.
.
Решая систему уравнений
получаем 
. Следовательно, исходный определитель равен
. ∎
Задание 8.
Вычислить ранг матрицы A: а) методом окаймляющих миноров; б) методом элементарных преобразований.
Решение.
а) Метод окаймляющих миноров.
Шаг 1. Выбираем ненулевой минор 1-го порядка: 
.
Шаг 2. Ищем ненулевой минор 2-го порядка, окаймляющий минор 
:
.
Шаг 3. Ищем ненулевой минор 3-го порядка, окаймляющий минор 
. Всего окаймляющих миноров 6:
, 
, 
,
, 
, 
.
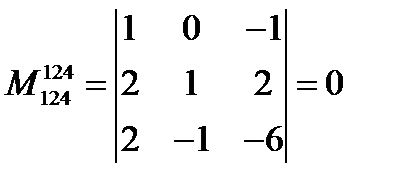Таким образом, все окаймляющие миноры 3-го порядка оказались равными нулю. Следовательно, ранг матрицы равен нулю.
|
|
б) Метод элементарных преобразований.
Количество ненулевых строк в получившейся ступенчатой матрице равно 2 и 
. ∎
Задание 9.
Найти обратную матрицу A: а) методом присоединенной матрицы; б) методом элементарных преобразований, если:
Решение. а) Вычисляем определитель 
. Следовательно обратная матрица существует.
2) Ищем алгебраические дополнения исходной матрицы (не забывать учитывать знаки алгебраических дополнений!):
| 
| 
|
| 
| 
|
| 
| 
|
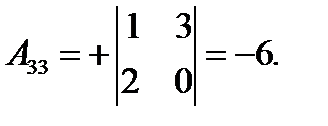
3) Составляем присоединенную матрицу:
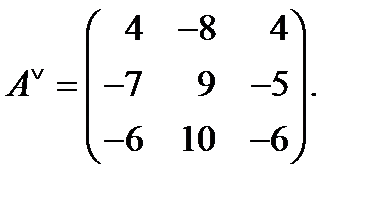
4) Записываем обратную матрицу:
5) Делаем проверку: 
:
Следовательно, обратная матрица найдена правильно. à
б) Образуем расширенную матрицу, приписав справа к матрице А единичную матрицу Е. После этого произведем элементарные преобразования строк:
.
Следовательно,
∎
Задание 10.
Решить матричное уравнение:
а) 
, где 
;
б) 
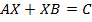, где 
.
Решение. а) Находим обратные матрицы:
.
Решение уравнения находим по формуле
. ∎
б) Запишем матрицу X поэлементно:
.
Тогда в подробной записи матричное уравнение примет вид:
.
Вычислив произведения матриц в левой части уравнения и сложив эти произведения, придем к уравнению
.
Записывая это матричное равенство по элементам, получим следующую систему линейных уравнений:
Следовательно, искомая матрица имеет вид:
.
Задание 11.
Найти решение СЛАУ: а) методом Крамера; б) при помощи обратной матрицы; в) методом Гаусса.
Решение.
а) Метод Крамера. Вычисляем определитель основной матрицы системы
.
Поскольку определитель D¹0, то система имеет единственное решение, которое можно найти по формулам
|
|
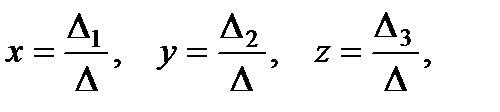
где D i – определитель матрицы, получаемой из основной, путем замены i -го столбца столбцом свободных членов:
, 
, 
.
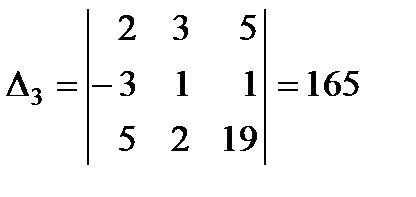Таким образом,
Сделаем проверку,
Следовательно, исходная система имеет решение: 
.
б) Метод обратной матрицы. Запишем исходную систему уравнений в матричном виде:
.
Тогда решение можно формально записать в виде:
.
Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу
.
Найдем ее
1) Вычисляем определитель исходной матрицы: 
.
2) Находим все алгебраические дополнения транспонированной матрицы:
 ,
|  ,
|  ,
|
 ,
|  ,
|  ,
|
 ,
|  ,
|  .
|
3) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:
.
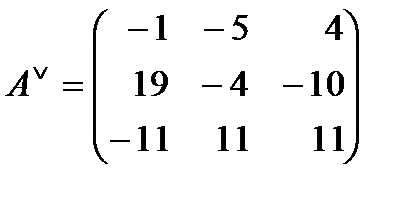4) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:
.
5) Сделаем проверку:
.
Следовательно, обратная матрица найдена правильно.
Теперь, используя найденную обратную матрицу можно найти решение исходной системы:
.
Как и следовало ожидать: 
.
в) Метод Гаусса. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее к треугольному виду:
| -3 |
.
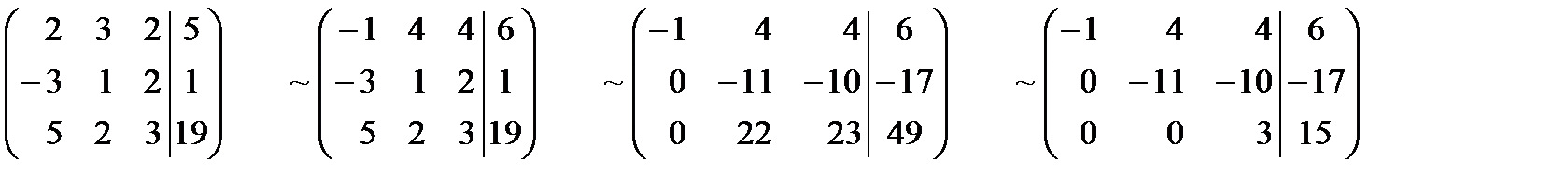Теперь выписываем соответствующую укороченную систему уравнений. Из последнего уравнения, находим значение z и подставляем его во второе уравнение; после этого из второго уравнения находим y; найденные значения x и y подставляем в первое уравнение, из которого затем находим значение x.
Задание 12.
Найти решение СЛАУ: а) методом Крамера; б) методом Гаусса.
Решение.
а) Метод Крамера. Вычисляем определитель основной матрицы системы
.
Поскольку определитель D¹0, то система имеет единственное решение, которое можно найти по формулам
,
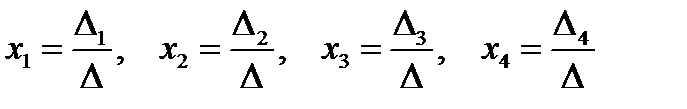где D i – определитель матрицы, получаемой из основной, путем замены i -го столбца столбцом свободных членов:
, 
, 
,
.
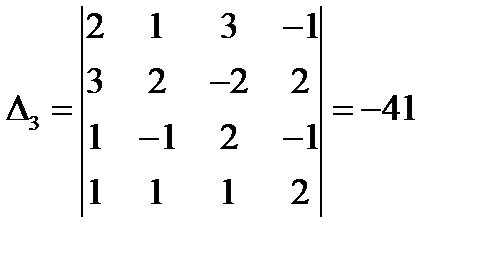Таким образом,
б) Метод Гаусса. Записываем расширенную матрицу
.
.
В результате получаем
Задание 13
Найти общее решение методом Гаусса
Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее трапециевидной форме:
| -1 |
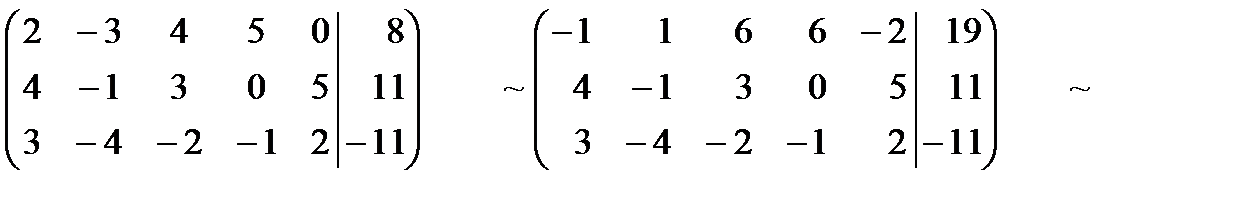
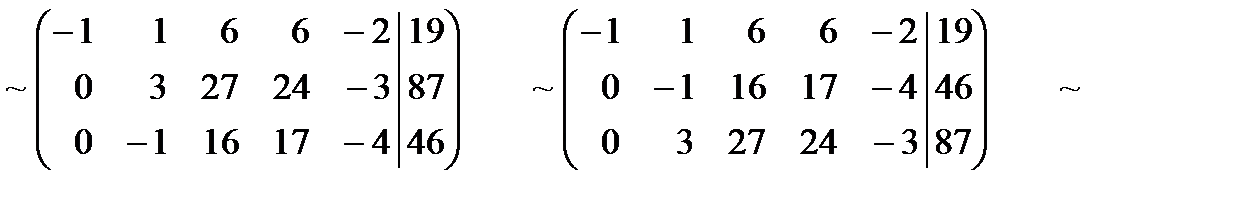
| :15 |
.
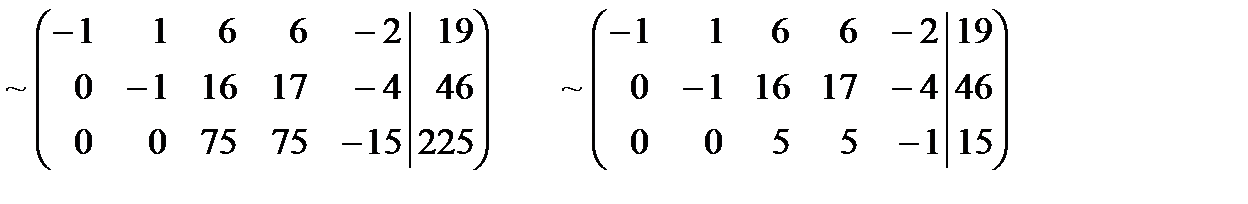Теперь выписываем соответствующую укороченную систему уравнений.
Пусть переменные x 4 и x 5 будут свободными, тогда переменные x 1, x 2 и x 3 будут основными, которые мы перенесем в правую часть:
Разрешая эту систему относительно x 1, x 2 и x 3 получим
Это есть общее решение системы. Запишем это решение в параметрическом виде. Пусть x 4= a и x 5=5 b, то общее решение системы запишется в виде:
Задание 14
Найти фундаментальную систему решений и общее решение однородной СЛАУ
Решение. Ранг матрицы системы равен 2. В качестве базисного минора выберем минор
.
Тогда переменные x 1, x 2 будут базисными, в переменные x 3, x 4 – свободными. Переписываем систему уравнений следующим образом:
Находим фундаментальную систему решений:
1) полагая 
, находим 
;
2) полагая 
, находим 
.
В результате получим фундаментальную систему решений
.
Записываем общее решение однородной СЛАУ:
. ∎
Задание 15
При каких значениях параметров a и b система имеет бесконечное множество решений? Найти эти решения.
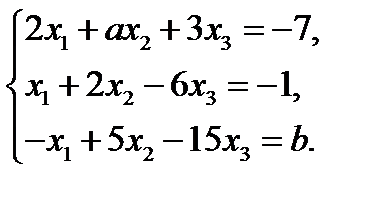
Решение. Найдем определитель системы:
.
Если 
, то по теореме Крамера система имеет единственное решение. Поэтому полагаем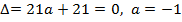 
. Найдем ранг расширенной матрицы
.
Если 
, то 
. В этом случае система несовместна. Положим 
, тогда 
. Следовательно, система имеет бесконечно много решений. Выберем в качестве базисных переменных x 1 и x 2, а качестве свободной – x 3. Оставляя первые два уравнения, получим
Таким образом, при 
система имеет бесконечно много решений, общее решение которой можно записать в виде:
∎
Задание 16-18
Применение СЛАУ для расчета
линейных электрических цепей
Расчет линейных электрических цепей постоянного тока
Состояние любой линейной электрической цепи можно описать СЛАУ, которая записывается в различных формах в зависимости от выбора переменных. Основными методами составления уравнений состояния электрической цепи являются методы контурных токов и узловых потенциалов, основанные на законах Ома и Кирхгофа. Закон Ома устанавливает напряжения U и тока I на участке цепи: 
или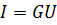 
, где R – сопротивление, 
– проводимость участка цепи. Первый закон Кирхгофа применяется к узлам: алгебраическая сумма токов в любом узле равна нулю, 
. Второй закон Кирхгофа применяется к замкнутым контурам: в любом контуре алгебраическая сумма напряжений на всех ветвях равна нулю, 
.
Метод контурных токов основан на использовании второго закона Кирхгофа. В качестве переменных здесь беру замкнутые контурные токи. Число уравнений, записываемых для контурных токов по второму Кирхгофа, равно числу независимых контуров, т.е. 
, где nв – число ветвей, nу – число узлов в схеме.
Метод узловых потенциалов основан на применении первого закона Кирхгофа. В качестве переменных здесь применяются напряжения (потенциалы) 
независимых узлов относительно одного узла, выбранного в качестве базисного.
Пример 5.6.1. Пользуясь методами контурных токов и узловых потенциалов, определить ток в диагонали мостовой схемы (рис. 5.6.1), где 
Ом, 
Ом, 
Ом, 
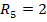Ом, 
Ом, 
Ом, 
В.
Рис. 5.6.1
Решение. а) Метод контурных токов. Число узлов в схеме равно 
, а число ветвей 
. Следовательно, схема содержит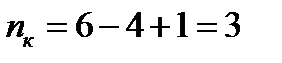 
независимых контура. Выберем эти три контура и зададим в каждом из них направление контурного тока (на схеме направления контурных токов I 1, I 2 и I 3 указаны стрелками). В соответствии со вторым законом Кирхгофа составляем уравнения для каждого контура, обходя их в направлении собственных контурных токов и учитывая напряжения от всех контурных токов. Так, при обходе первого контура против часовой стрелки получаем, что напряжение на сопротивлении R 1 равно 
, на R 2 –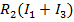 
, на R 5 – 
. Поскольку в этом контуре нет ЭДС, то сумма всех этих напряжений равна нулю:
.
Аналогично получаем уравнения для второго и третьего контуров, соотетственно:
, 
.
В результате имеем следующую систему линейных уравнений относительно токов:
Подставляя числовые значения, получим
Тогда искомый ток в диагонали мостовой схемы равен разности контурных токов: 
А и совпадает по направлению с контурным током I 2.
б) Метод узловых потенциалов. Заданная схема содержит 4 узла, из них 3 независимых. Выберем в качестве базисного узел 4, т.е. положим, что в этом узле потенциал 
. В соответствии с первым законом Кирхгофа составляем уравнения для каждого независимого узла, учитывая, что суммы токов ветвей, подходящих или выходящих из каждого узла, равна нулю. Так, для первого узла по ветви с сопротивлением R 2 выходит ток 
, по ветви с сопротивлением R 1 – ток 
, по ветви с сопротивлением R 6 – ток 
. В результате имеем
.
Аналогично получаем уравнения для второго и третьего, соответственно:
, 
.
В результате имеем следующую систему линейных уравнений относительно потенциалов:
где 
– проводимость ветвей схемы. Подставляя численные значения, получим
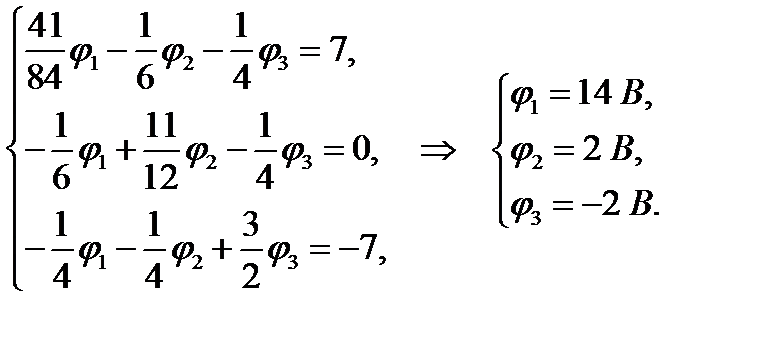
Поскольку падение напряжения между узлами 2 и 4, т.е. напряжение на сопротивлении R 5, равно 
В, то искомый ток будет 
А. ∎