Расчет центрально-растянутых элементов: - в фермах, арках, т.е. в покрытиях.
Расчет - с учетом имеющихся ослаблений сечения. При нахождении площади следует учитывать ослабления, расположенные по длине до 200мм, т.к. они совместно могут служить причиной разрыва стержня.
 , где
, где 
 -расчетная продольная сила;
-расчетная продольная сила;  -площадь поперечного сечения элемента нетто;
-площадь поперечного сечения элемента нетто;
 - расчетное сопротивление древесины растяжению вдоль волокон;
- расчетное сопротивление древесины растяжению вдоль волокон;


Наличие ослаблений приводит к возникновению конценрации напряжений, что может явиться причиной снижения несущей способности элемента. Следовательно учитывается в расчете введением коэффициента условий работы у = 0,8
Расчет центрально-сжатых элементов:
Вследствие вязкой работы на сжатие концентрация напряжений у мест ослаблений существенно не оказывает влияния на снижение сопротивляемости элементов.
Расчет ц-сж элементов постоянного сечения следует производить по формулам:
а) На прочность  б) на устойчивость
б) на устойчивость 
 – расчет сопрот древесины сжатию вдоль волокон;
– расчет сопрот древесины сжатию вдоль волокон;
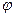 - коэффициент продольного изгиба, и зависит от гибкости, определяется по графику, по таблицам, по формулам.
- коэффициент продольного изгиба, и зависит от гибкости, определяется по графику, по таблицам, по формулам.
Для дерева гибкость определяется по формуле:  ,
, 
 ,
, 
где а - коэффициент для древесины а=0,8, для фанеры а=1, коэффициент А=3000 –для древесины; А=2500 – для фанеры
Гибкость элементов цельного сечения определяют по формуле 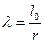 , l0-расчетная длина элемента; r-радиус инерции сечения элемента с максимальными размерами брутто соответственно осей Х или У.
, l0-расчетная длина элемента; r-радиус инерции сечения элемента с максимальными размерами брутто соответственно осей Х или У. 
Расчет длина элементов 
 берем из СНиП табл 14, с учетом назначения сжатого элемента, определяем предельную гибкость, т.е. максимальную гибкость (
берем из СНиП табл 14, с учетом назначения сжатого элемента, определяем предельную гибкость, т.е. максимальную гибкость ( )
) 

При отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (а), если площадь ослаблений не превышает 25% Fбр, Fрас= Fбр, где Fбр – площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% Fбр, Fрас=4/3Fнт,
При симметричных ослаблениях, выходящих на кромки (б), Fрас= Fнт,
3. Расчет изогнутых, сжато-изогнутых и растянуто-изогнутых деревянных элементов цельного сечения.
В изгибаемом элементе от нагрузок, действующих поперек его продольной оси, возникают изгибающие моменты и поперечные силы, определяемые методами строительной механики. Например, в середине пролета l однопролетной балки от равномерной нагрузки q возникает изгибающий момент  . От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба
. От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба  , которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается.
, которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается.
Древесина работает на изгиб достаточно надежно и момент имеет вторую категорию качества. На рис 1. показаны стандартный образец древесины и диаграмма его прогибов при испытании на изгиб. Диаграмма как и при сжатии, примерно до половины имеет линейное очертание, затем изгибается, показывая ускоренный рост прогибов. Разрушение образца начинается с появления складок крайних сжатых волокон и завершается разрывом крайних растянутых, в результате чего образец ломается при среднем напряжении изгиба.
Нормальные напряжения в сечениях изгибаемого элемента распределяется неравномерно по высоте. В начальной расчетной стадии древесина работает упруго и эпюра напряжений изображается прямой линией, показывающей максимальные напряжения сжатия и растяжения у кромок и нулевые у нейтральной оси сечения. При дальнейшем нагружении сжатая часть сечения начинает работать упругопластично, эпюра изгибается и нейтральная ось смещается в сторону растяжения. В стадии разрушения сжатая часть эпюры изгибается еще больше, напряжения сжатия и растяжения достигают предела прочности и элемент ломается.


Изгибаемые элементы рассчитывают по несущей способности: прочности на действие изгибающих моментов и поперечных сил от расчетных нагрузок и по прогибам от нормативные нагрузок. Их прочность и жесткость зависят от размеров и форм поперечных сечений, определяющих их геометрические характеристики – момент инерции, момент сопротивления и статический момент.
Для распространенных сечений деревянных элементов они равны: для прямоугольного с размерами b, h,  ; Для круглого диаметром d
; Для круглого диаметром d  ;
;
Площади ослаблений при вычислении I и S исключается.
Проверку изгибаемого элемента по прочности по нормальным напряжениям производят на действие максимального изгибающего момента от расчетных нагрузок по формуле  , где
, где
М- расчет изгиб момент; Ru –расч сопрот изгибу; Wрасч – расч момент сопрот поперечного сечения элемента.
Для цельных элементов Wрасч= Wнт; для изгибаемых составных элементов на податливых соединениях расчетный момент сопротивления принимают равным моменту сопротивления нетто Wнт, умноженному на коэффициент kw; значение kw для элементов, составляемых из одинаковых слоев, приведены в СНиП. При определении Wн ослабления сечений, расположенные на участке элемента длиной до 200мм, принимают совмещенными в одном сечении.
Подбор сечения изгибаемого элемента по прочности производят по этой же формуле, но относительно требуемого момента сопротивления Wтр, после чего задается один из размеров прямоугольного сечения, b или h, и определяется другой или вычисляется диаметр круглого сечения d по формулам: 
Предельная расчетная нагрузка, которую может выдерживать изгибаемый элемент по прочности, когда все его размеры известны, может быть вычислена по формуле  , но относительно изгибающего момента М. Например, однопролетная балка пролетом l, с размерами bh может выдерживать равномерную нагрузку, определяемую в следующем порядке:
, но относительно изгибающего момента М. Например, однопролетная балка пролетом l, с размерами bh может выдерживать равномерную нагрузку, определяемую в следующем порядке: 
Расчет изгибаемого элемента по прогибам заключается в определении его наибольшего относительного прогиба  от нормативных нагрузок и проверке его значения (чтобы оно не превосходило предельного допускаемого нормами), т.е..
от нормативных нагрузок и проверке его значения (чтобы оно не превосходило предельного допускаемого нормами), т.е..
Относительный прогиб однопролетной балки при равномерной нормативной нагрузке равен: 
При определении прогиба необходимо соблюдать единую размерность: l,м; Е=10000 МПа; I, м4; q, МН/м;
Если относительный прогиб балки, сечения которой подобрано по прочности, получается больше предельного, сечение д.б. увеличено и подобрано по прогибу, для чего формула прогиба д.б. переписана относительно требуемого момента инерции. Для однопролетной балки при равномерной нагрузке 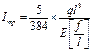 ; после этого можно задаться одним размером прямоугольного сечения и вычислить другой. Прочность древесины балок, сечение которого подобрано по прогибу, используется не полностью. Прямоугольные изгибаемые элементы выгоднее располагать большими сторонами сечения h в направлении действия нагрузки, поскольку их момент сопротивления пропорционален квадрату. А момент – кубу высоты.
; после этого можно задаться одним размером прямоугольного сечения и вычислить другой. Прочность древесины балок, сечение которого подобрано по прогибу, используется не полностью. Прямоугольные изгибаемые элементы выгоднее располагать большими сторонами сечения h в направлении действия нагрузки, поскольку их момент сопротивления пропорционален квадрату. А момент – кубу высоты.
Расчет изгибаемых элементов на прочность по скалыванию (расчет изгибаемых элементов на прочность по максимальным касательным напряжениям):В изгибаемых элементах от действия поперечных сил возникают сдвигающие силы Т и напряжения скалывания, равномерные по ширине сечений. По длине элемента они изменяются пропорционально поперечным силам и достигают максимума у опор, где в однопролетной балке при равномерной нагрузке  .
.
По высоте сечений скалывающие напряжения распределяются неравномерно, возрастая от нулевых у кромок до максимальных у нейтральной оси. Они зависят прямо пропорционально от поперечной силы и статического момента скалываемой части сечения и обратно пропорционально от момента инерции и ширины сечения.

I – момент инерции сечения брутто относительно нейтральной оси;
S – статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;
Rск –расчетное сопротивление скалыванию при изгибе;
B – расчетная ширина сечения элемента;
Q –расчетная поперечная сила;
Расчет элементов цельного сечения на прочность при косом изгибе: косой изгиб возникает в элементах, оси сечений которых расположены наклонно к направлению нагрузок, например, в брусчатых прогонах скатных покрытий. При косом изгибе нормальные напряжения в сечениях суммируются и достигают максимальных значений сжатия только в верхнем, а растяжение – в нижнем углах прямоугольного сечения. Вертикальная нагрузка, например q, и изгибающие моменты при косом изгибе вдоль  раскладываются на нормальную и скатную составляющие вдоль сечения:
раскладываются на нормальную и скатную составляющие вдоль сечения: 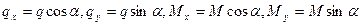 . Относительно этих осей определяют моменты инерции Iх и Iу и моменты сопротивления Wх и Wу сечений. Проверку прочности при косом изгибе производятпо формуле:
. Относительно этих осей определяют моменты инерции Iх и Iу и моменты сопротивления Wх и Wу сечений. Проверку прочности при косом изгибе производятпо формуле: 
Мх и Му –составляющие расчетного изгибающего момента для главных осей сечения х и у;
Wх и Wу – моменты сопротивления поперечного сечения нетто относительно главных осей сечения х и у;
Подбор сечений косоизгибаемых элементов производят методом попыток, причем их следует устанавливать большими размерами сечений в направлении действия больших составляющих нагрузок. Расчет по прогибам производят с учетом геометрической суммы прогибов относительно каждой из осей сечений:
Прогибы при косом изгибе: 
Расчет сжато-изогнутых элементов: Элементы, находящиеся при одновременном действии сжимающей нормальной силы и изгибающего момента, например рамы и арки, называют сжато-изгибаемыми.
В сечениях сжато-изгибаемого элемента возникают равномерные напряжения сжатия от продольных сил и напряжения сжатия и растяжения от изгибающего момента, которые суммируются.

Максимальные напряжения сжатия  возникают в крайних волокнах сечений со стороны сжатия от изгиба. Разрушение сжато-изгибаемого элемента начинается с появления складок волокон в месте действия максимальных сжимающих напряжений и заканчивается разрывом растянутых волокон с противоположной стороны.
возникают в крайних волокнах сечений со стороны сжатия от изгиба. Разрушение сжато-изгибаемого элемента начинается с появления складок волокон в месте действия максимальных сжимающих напряжений и заканчивается разрывом растянутых волокон с противоположной стороны.
МД – изгибающий момент от действия поперечных и продольных нагрузок, определяемый из расчета по деформированной схеме.
Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического, полигонального и близких к ним очертаний, а также для консольных элементов МД определяется по формуле:
МД=М/  kн, где kн =1
kн, где kн =1
Для шарнирно-опертых элементов с эпюрами изгибающих моментов треугольного и прямоуг. очертаний: kн =  +
+  (1-
(1-  )
)
 =1,22 – коэффициент, который принимается при эпюрах изгибающих моментов треугольного очертания и 0,81- при эпюрах прямоугольного очертания (от постоянного изгибающего момента).
=1,22 – коэффициент, который принимается при эпюрах изгибающих моментов треугольного очертания и 0,81- при эпюрах прямоугольного очертания (от постоянного изгибающего момента).
 - коэффициент, изменяющий от1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента;
- коэффициент, изменяющий от1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента;
 , где М – изг. момент в расчетном сечении без учета дополнительного момента от продольной силы;
, где М – изг. момент в расчетном сечении без учета дополнительного момента от продольной силы;
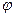 - коэффициент продольного изгиба;
- коэффициент продольного изгиба;
Fбр – площадь поперечного сечения элемента, принимая по наибольшему значению высоты сечения h.
При несимметричном загружении шарнирно-опертых элементов
МД=Мс/ 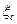 + Мк/
+ Мк/ 
Мс, 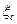 , Мк,
, Мк,  - изгибающие моменты в расчетном сечении элемента и коэффициенты определяемые по формуле при значениях гибкостей, соответствующих симметричной и кососимметричной нагрузкам и формам продольного изгиба;
- изгибающие моменты в расчетном сечении элемента и коэффициенты определяемые по формуле при значениях гибкостей, соответствующих симметричной и кососимметричной нагрузкам и формам продольного изгиба;
При Мс/  расчет плоскости изгиба выполняют по формуле
расчет плоскости изгиба выполняют по формуле  без учета изгибающего момента;
без учета изгибающего момента;
Проверяют элементы по касательным напряжениям по формуле  , поставляя вместо Q значение Qвн= Q/
, поставляя вместо Q значение Qвн= Q/  ,
,
а прогиб  , где f и
, где f и  определяются по СНиП.
определяются по СНиП.
Сжато-изгибаемые элементы прямоугольного поперечного сечения рассчитывают на устойчивость плоской формы деформирования  , где F и W – максимальные значения соответственно площади и момента сопротивления поперечного сечения на рассматриваемом участке l0 сечения;
, где F и W – максимальные значения соответственно площади и момента сопротивления поперечного сечения на рассматриваемом участке l0 сечения; 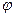 у –коэффициент продольного изгиба для гибкости участка элемента расчетной длиной l0 в плоскости, перпендикулярнорй плоскости деформирования, которые определяются для древесины в СНиП, с умножением на коэффициент kжМ; kжМ - коэффициент, учитывающий переменность высоты сечения по длине элемента, не закрепленного их плоскости по растянутой от момента кромке или при числе подкрепленных точек растянутой кромке менее четырех;
у –коэффициент продольного изгиба для гибкости участка элемента расчетной длиной l0 в плоскости, перпендикулярнорй плоскости деформирования, которые определяются для древесины в СНиП, с умножением на коэффициент kжМ; kжМ - коэффициент, учитывающий переменность высоты сечения по длине элемента, не закрепленного их плоскости по растянутой от момента кромке или при числе подкрепленных точек растянутой кромке менее четырех; 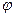 м – по кромки из плоскости деформирования, n=1 –для элементов с закрепленной растянутой кромкой. Определяется по формуле из СНиП.
м – по кромки из плоскости деформирования, n=1 –для элементов с закрепленной растянутой кромкой. Определяется по формуле из СНиП.
-Задаемся размерами bh по сортаменту;
-находим геометрические характеристики F,W,N,M; -находим 
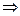 гибкость
гибкость  радиус инерции
радиус инерции  ;
;
-находим Мд 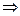
 ; проверяем устойчивость;
; проверяем устойчивость;
Растянуто-изогнутые элементы: Элементы, находящиеся при одновременном действии растягивающей продольной силы и изгибающего момента (например, нижний пояс фермы с подвесным потолком), называют растянуто-изгибаемыми.
В сечениях растянуто- изгибаемого элемента от продольной растягивающей силы возникают равномерные растягивающие напряжения, а от изгибающего момента М –напряжения изгиба, состоящие из сжатия на одной стороне сечения и растяжения на другой. Эти напряжения суммируются чему растягивающие напряжения увеличиваются, сжимающие уменьшаются. Наибольшие напряжения растяжения возникают в крайних сечениях в местах действия максимального момента. Следовательно начинается разрушение элемента от разрыва растянутых волокон древесины.
 Wрас – расчетный момент сопротивления поперечного сечения;
Wрас – расчетный момент сопротивления поперечного сечения;
Fрас – площадь расчетного сечения нетто;