(Прямая задача теории погрешностей)
Прямая (основная) задача теории погрешностей заключается в вычислении погрешности результата математических действий, если известны погрешности аргументов. При этом действия над аргументами можно представить в виде функции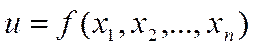 
,
- дифференцируемая функция;
- предельные абсолютные погрешности аргументов 
.
Предельная абсолютная погрешность функции
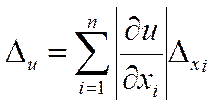, (1.12)
Предельная относительная погрешность функции
(1.13)
Формула (1.13) получена путем деления (1.12) на модуль 
.
Пример 1.1
, 
Из этого следует, что предельная абсолютная погрешность суммы, не может быть меньше предельной абсолютной погрешности наименее точного (в смысле абсолютной погрешности) из слагаемых, т.е. слагаемого, имеющего максимальную абсолютную погрешность. Следовательно, с какой бы степенью точности не были определены остальные слагаемые, мы не можем за их счет увеличить точность суммы. Поэтому не имеет смысла сохранять излишние знаки и в более точных слагаемых. Отсюда вытекает следующее, обычно применяемое, практическое правило для сложения приближенных чисел:
- выделить числа, десятичная запись
которых обрывается ранее других и оставить
без изменения;
- остальные числа округлить по образцу выделенных, сохраняя один или два
запасных десятичных знака;
- произвести сложение данных чисел,
учитывая все сохраненные знаки;
- полученный результат округлить на один
знак.
Пример 1.2
, 
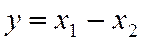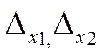
Из результата вычисления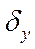 
вытекает, что 
может быть весьма большой, если приближенные числа 
и 
достаточно близки друг к другу, в то время как их погрешности (абсолютные и относительные) остаются малыми, т.е. т.о. происходит потеря точности.
|
|
Исходя из вышесказанного, получаем еще одно практическое правило:
- при приближенных вычислениях следует избегать вычитания двух почти равных приближенных чисел;
- если же приходится вычитать такие числа, то следует преобразовывать такие выражения, или (если такая возможность имеется) уменьшаемое и вычитаемое брать с достаточным числом запасных верных знаков.
Т.о., примеры на определение погрешности суммы, разности, произведения, частного, корня, степени дали возможность выработать рекомендации по выполнению массовых вычислений (без точного учета погрешностей):
- при сложении и вычитании младший сохраненный десятичный разряд результата должен являться наибольшим среди десятичных разрядов, выражаемых последними значащими цифрами исходных данных;
- при умножении, делении следует сохранять столько значащих цифр, сколько их имеет исходное данное с наименьшим числом верных цифр;
- при возведении в степень следует сохранять столько значащих цифр, сколько верных цифр основания степени.
- при извлечении корня в результате следует брать столько значащих цифр, сколько верных цифр имеет подкоренное выражение;
- если некоторые данные имеют излишние младшие десятичные разряды (при сложении и вычитании) или больше значащих цифр, чем другие (при умножении, делении, возведении в степень, извлечении корня), то их предварительно нужно округлить, сохраняя одну (две) запасные цифры;
- во всех промежуточных результатах следует сохранять на одну (две) цифры больше, чем рекомендуют предыдущие правила, в окончательном результате одна из оставленных цифр отбрасывается.
|
|
Обратная задача теории
Погрешностей