1. Испытательные машины 100 кН или 300 кН (10 т.с. или 30 т.с.): УИМ -10 или УИМ – 30.
2. Штангенциркуль и масштабная линейка
Образцы
Цилиндры из модельного материала размерами: диаметром - d = 25 мм и высотой - h = 30 мм с рисками в виде цилиндрических кругов на торцах.
Измерения и ход работы
На бригаду выдаются два цилиндрических образца. С помощью штангенциркуля измеряют их высоты и диаметры. Концентрические окружности на торцах образцов, нанесённые для выявления относительной протяжённости зоны прилипания ( ), замеряют с использованием масштабной линейки. Для того, чтобы исключить влияние на результаты опытов овальности концентрических окружностей, которая может иметь место, замеры их до и после осадки необходимо производить по одному направлению. Для этого на торце по диаметру окружностей проводится риска, по риске и производят все измерения диаметров концентрических окружностей. Кроме того, для наблюдения за переходом металла при осадке с боковой поверхности на контактную проводится риска по образующей цилиндров до самых их торцов. Для того, чтобы риски оставались заметными и после осадки, их предварительно заполняют меловым порошком.
), замеряют с использованием масштабной линейки. Для того, чтобы исключить влияние на результаты опытов овальности концентрических окружностей, которая может иметь место, замеры их до и после осадки необходимо производить по одному направлению. Для этого на торце по диаметру окружностей проводится риска, по риске и производят все измерения диаметров концентрических окружностей. Кроме того, для наблюдения за переходом металла при осадке с боковой поверхности на контактную проводится риска по образующей цилиндров до самых их торцов. Для того, чтобы риски оставались заметными и после осадки, их предварительно заполняют меловым порошком.
Для избежания дополнительных погрешностей все измерения необходимо производить одним и тем же инструментом.
Один из образцов осаживают на шероховатых бойках, то есть при наличии значительных сил внешнего трения.
Образец осаживают на 40% - 50% ( ), после чего определяют его размеры, а также диаметры концентрических окружностей (
), после чего определяют его размеры, а также диаметры концентрических окружностей ( ), нанесённые на его торце. Диаметр зоны прилипания считают равным наибольшему из не изменивших после осадки своих размеров диаметру концентрических окружностей на контактной поверхности образца. Следует иметь ввиду, что диаметры окружностей внутри зоны прилипания тоже не будут изменяться.
), нанесённые на его торце. Диаметр зоны прилипания считают равным наибольшему из не изменивших после осадки своих размеров диаметру концентрических окружностей на контактной поверхности образца. Следует иметь ввиду, что диаметры окружностей внутри зоны прилипания тоже не будут изменяться.
Для установления отношения  , характеризующего форму цилиндрического образца после неравномерной осадки определяют среднее значение диаметра (
, характеризующего форму цилиндрического образца после неравномерной осадки определяют среднее значение диаметра (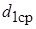 ) цилиндра, принявшего бочкообразную форму. С этой целью замеряют диаметр всей контактной поверхности
) цилиндра, принявшего бочкообразную форму. С этой целью замеряют диаметр всей контактной поверхности 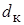 и максимальный диаметр по середине высоты -
и максимальный диаметр по середине высоты -  . Тогда
. Тогда
 ,
,
либо, точнее
 .
.
Проконтролировать правильность замеров образца после деформации можно расчётом, пользуясь условием несжимаемости (постоянства объёма).

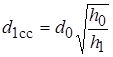 .
. 
Второй образец осаживают на полированных, смазанных маслом бойках до той же степени деформации, что и у предыдущего образца. Целесообразно периодически возобновлять смазку, поскольку она выдавливается из-под бойков в процессе осадки. Все замеры производятся аналогично.
В том случае, когда предполагается установить зависимость относительного диаметра зоны прилипания  от формы цилиндра
от формы цилиндра  все операции по осадке и замеру образцов производят точно также. Отличие состоит лишь в следующем: образцы осаживают не сразу на 40% - 50%, а ступенями по 30% от конечной высоты после предыдущей осадки. Таких осадок делают 2 – 3 для каждого из образцов, причём один из них осаживают всё время на шероховатых, а второй на полированных бойках со смазкой.
все операции по осадке и замеру образцов производят точно также. Отличие состоит лишь в следующем: образцы осаживают не сразу на 40% - 50%, а ступенями по 30% от конечной высоты после предыдущей осадки. Таких осадок делают 2 – 3 для каждого из образцов, причём один из них осаживают всё время на шероховатых, а второй на полированных бойках со смазкой.
Для каждого из образцов после каждой из осадок устанавливают величины отношений  и
и  .
.
Результаты всех измерений сводят в таблицу опытных данных.
В отчёте необходимо отметить цели работы, привести зарисовки контуров цилиндрических образцов до и после деформации, кратко изложить последовательность выполнения работы, дать описание однородной и неоднородной деформации с указанием внешних их проявлений; отметить влияние внешнего трения на схему напряжённого состояния в обоих случаях. Установить зависимость  от формы цилиндра, представив её в виде графика. Установить качественную зависимость относительной зоны прилипания от коэффициента внешнего трения.
от формы цилиндра, представив её в виде графика. Установить качественную зависимость относительной зоны прилипания от коэффициента внешнего трения.
Таблица 1.1
Таблица опытных данных по осадке цилиндрических образцов
| № об | № оп |  мм
мм
|  мм
мм
|  , мм , мм
|  , мм , мм
|  мм
мм
|  мм
мм
|  мм
мм
|  мм
мм
|  мм
мм
| 
|  мм
мм
| 
| Условия осадки | ||||||
2. РАБОТА №2. ВЛИЯНИЕ ВНЕШНЕГО ТРЕНИЯ НА ФОРМОИЗМЕНЕНИЕ ПАРАЛЛЕЛЕПИПЕДА ПРИ ОСАДКЕ
2.1. Общие сведения
При осадке образцов прямоугольного поперечного сечения (параллелепипедов) на плоскопараллельных бойкахпри соответствующем состоянии деформирующих поверхностей наблюдаются те же внешние проявления, что и при осадке цилиндра: наличие или отсутствие зоны прилипания, приращение контактной поверхности либо за счёт скольжения, либо за счёт перехода с боковой поверхности на контактную, бочкообразование и т.д. Однако деформация в этом случае более сложна, так как прямоугольная полоса не является осесимметричным телом.


Рис.2.1. Прямоугольная полоса до осадки
Если на шероховатых бойках осаживать тело с поперечным сечением отличным от круга, например, прямоугольным, то наблюдается выпучивание сторон образца в поперечном и продольном направлениях. Вследствие выпучивания сторон параллелепипед принимает в плане форму эллипса, а при весьма значительных степенях деформации – стремится принять форму круга, то есть форму геометрической фигуры, имеющей наименьший периметр при данной площади. Этот факт формулируется в виде правила наименьшего периметра.
Это правило является следствием закона минимума энергии деформации или закона наименьшего сопротивления. Этот закон гласит: каждая точка деформируемого тела перемещается в том направлении, на котором затраты энергии на это перемещение будут минимальными или в случае возможности перемещения точек деформируемого тела в различных направлениях, каждая его точка перемещается в направлении наименьшего сопротивления со стороны внешних сил.
Силы внешнего трения (касательные напряжения на контактной поверхности) при осадке прямоугольной полосы и представляют собой сопротивления смещению металла относительно поверхности инструмента. При осадке параллелепипеда в условиях неоднородной деформации деформация в направлении короткой его стороны b оказывается большей, чем в направлении длинной стороны l, вследствие того, что в поперечном направлении сопротивление течению металла  меньше, чем в продольном направлении
меньше, чем в продольном направлении  . Или, что то же самое, перемещение в направлении ширины параллелепипеда требует меньших затрат энергии, чем перемещение в продольном направлении [1,2].
. Или, что то же самое, перемещение в направлении ширины параллелепипеда требует меньших затрат энергии, чем перемещение в продольном направлении [1,2].
Это положение можно проиллюстрировать схемой, приведённой на рис.2.2.
В соответствии со схемой сопротивление перемещениям точки A в поперечном и продольном направлениях могут быть соответственно записаны так:
 ,
,
 .
.
Здесь  - коэффициент внешнего трения, p - удельное давление, b ' и l '- расстояние от точки A соответственно до длинной и короткой стороны параллелепипеда.
- коэффициент внешнего трения, p - удельное давление, b ' и l '- расстояние от точки A соответственно до длинной и короткой стороны параллелепипеда.

Рис.2.2. Схема, иллюстрирующая влияние сил внешнего трения на изменение формы поперечного сечения прямоугольной полосы при осадке
Поскольку для точки A и всех других точек, расположенных в трапециевидных зонах поперечного сечения полосы b ' < l ', то при постоянных
значениях  ,
,  . Отсюда следует, что с увеличением
. Отсюда следует, что с увеличением  большая часть металла, смещённого по высоте, будет перемещаться в поперечном направлении, ибо при этом возрастает относительная протяжённость (длина) зон уширения, растёт и величина l. Соответственно, уменьшение
большая часть металла, смещённого по высоте, будет перемещаться в поперечном направлении, ибо при этом возрастает относительная протяжённость (длина) зон уширения, растёт и величина l. Соответственно, уменьшение 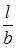 вызовет уменьшение поперечного течения металла. Естественно, что при этом изменятся и энергетические затраты, также обусловливающие характер перемещений в направлении l и b.
вызовет уменьшение поперечного течения металла. Естественно, что при этом изменятся и энергетические затраты, также обусловливающие характер перемещений в направлении l и b.
В связи с более интенсивным приращением ширины основания прямоугольной полосы происходит постепенное выравнивание сопротивлений течению металла в различных горизонтальных направлениях. Круг – единственная форма поперечного сечения тела, у которого по всем направлениям или по всем радиусам сопротивления (энергетические затраты перемещения) одинаковы. Поэтому при осадке прямоугольной полосы на шероховатых бойках и соблюдается правило наименьшего периметра (рис.2.3)

Рис.2.3. Схема постепенного перехода прямоугольного сечения в круглое
При идеальной осадке, то есть при f =0, имеет место линейное напряжённое состояние. Силы внешнего трения, представляющие собой сопротивления течению металла, отсутствуют. В связи с этим форма горизонтального поперечного сечения прямоугольного параллелепипеда сохранится при любой величине деформации.
Можно показать, что при идеальной осадке параллелепипеда отношение сторон его основания остаётся постоянным, то есть  . Поскольку форма поперечного сечения после однородной деформации сохраняется прямоугольной, а отношения его сторон - постоянными, можно сделать вывод о том, что форма продольного поперечного сечения прямоугольной полосы (параллелепипеда) остаётся геометрически подобной первоначальной.
. Поскольку форма поперечного сечения после однородной деформации сохраняется прямоугольной, а отношения его сторон - постоянными, можно сделать вывод о том, что форма продольного поперечного сечения прямоугольной полосы (параллелепипеда) остаётся геометрически подобной первоначальной.
Для любой формы сечения деформируемого тела, при однородной деформации поперечное сечение тела остаётся геометрически подобным первоначальному. Это формулировка правила подобия сечений. Правило подобия, как и правило наименьшего периметра, является частным случаем проявления закона наименьшего сопротивления, а в наиболее общей форме – принципа минимума энергии деформации.
В процессе осадки силы трения полностью устранить невозможно. Тем не менее, при помощи ряда приёмов можно существенно уменьшить их величину и таким путём добиться более равномерной деформации тела. К числу таких приёмов относятся: применение инструмента с поверхностью, обработанной по высокому классу чистоты; применение смазки; подбор надлежащих условий деформации, определяющих состояние тела: температуры, скорости деформации и обжатий; осадка между выпуклыми или коническими бойками и др. приёмы.
Естественно, что наличие больших или меньших по величине подпирающих сил внешнего трения или практически полное их отсутствие не могут не сказываться на величине усилий, которые требуются для деформации.
Рассчитать удельное давление можно, пользуясь следующей формулой [3]:
 ,
,
где 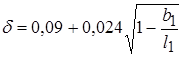 ;
;  ;
;
 ,
, 
 - соответственно высота, ширина и длина прямоугольной полосы в конечный момент деформации;
- соответственно высота, ширина и длина прямоугольной полосы в конечный момент деформации;  - предел текучести (сопротивление деформации) металла.
- предел текучести (сопротивление деформации) металла.
Сила осадки определяется как произведение удельного давления  на площадь F контактной поверхности полосы в конечный момент деформации
на площадь F контактной поверхности полосы в конечный момент деформации
 .
.
Цели работы
1. Проследить за формоизменением прямоугольных полос (параллелепипедов) при их осадке на плоско-параллельных бойках с разным состоянием рабочих поверхностей.
2. На практике последить за проявлениями правил наименьшего периметра и подобия.
3. Установить влияние внешнего трения на удельное давление при осадке прямоугольных полос.
Оборудование, аппаратура и инструмент
1. Испытательные машины 100 кН или 300 кН (10 т.с. или 30 т.с.): УИМ -10 или УИМ – 30.
2. Штангенциркуль.
Образцы
Параллелепипеды из модельного материала разных размеров:
 =
=  мм.
мм.
2.2. Измерения и ход работы
Два параллелепипеда, выданные на бригаду, предварительно замеряют с помощью штангенциркуля. Определяют размеры  ,
,  и
и 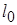 .
.
Один из образцов дважды осаживают на шероховатых бойках (при значительном коэффициенте внешнего трения); степень деформации каждый раз порядка 50%.
В момент окончания осадки фиксируют показания динамометра на прессе.
Поскольку в процессе осадки на шероховатых бойках форма продольного поперечного сечения параллелепипеда сильно искажается, измерения затрудняются. В частности, длину деформированного образца приходится брать как среднее арифметическое замеров  и
и 
 .
.
Ширину параллелепипеда определяют из условия несжимаемости (постоянства деформируемого объёма).
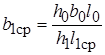 .
.
Второй образец тоже дважды осаживают на полированных смазанных бойках (в условиях, когда  ). После каждых 10% осадки целесообразно смазку на бойках возобновлять. Суммарная деформация как после первой, так и после второй осадки должна быть точно такой же, как и для образца, деформируемого на шероховатых бойках. Нужно при этом иметь в виду, что размеры обоих образцов после первой осадки (
). После каждых 10% осадки целесообразно смазку на бойках возобновлять. Суммарная деформация как после первой, так и после второй осадки должна быть точно такой же, как и для образца, деформируемого на шероховатых бойках. Нужно при этом иметь в виду, что размеры обоих образцов после первой осадки ( ,
,  и
и  ) являются начальными для второй осадки.
) являются начальными для второй осадки.
В связи с тем, что  , некоторое искажение продольного поперечного сучения полосы после осадки всё же происходит. Поэтому замеры продольных размеров необходимо также усреднять, а ширину деформированного параллелепипеда определять из условия несжимаемости (постоянства объёма).
, некоторое искажение продольного поперечного сучения полосы после осадки всё же происходит. Поэтому замеры продольных размеров необходимо также усреднять, а ширину деформированного параллелепипеда определять из условия несжимаемости (постоянства объёма).
На основании опытных данных определяют отношение  для однородной и неоднородной осадки.
для однородной и неоднородной осадки.
Сопоставление этих отношений для каждого из образцов с первоначальными значениями  даёт возможность установить степень соблюдения правила подобия сечений в каждом из случаев.
даёт возможность установить степень соблюдения правила подобия сечений в каждом из случаев.
Результаты всех измерений сводят в таблицу.
В отчёте отметить цели работы, привести зарисовки контуров продольных поперечных сечений полос до и после деформации, кратко изложить последовательность выполнения работы; сформулировать правила наименьшего периметра и подобия сечений. Сделать выводы о правиле подобия при осадке образцов с разным состоянием поверхности и о зависимости удельного давления от коэффициента внешнего трения.
Таблица 2.1
| № об | № оп | Данные опыта |
 МПа
МПа
|

| |||||||||||||
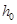 мм
мм
| 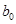 мм
мм
|  мм
мм
|  мм мм
| 
|  мм
мм
| 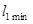 мм мм
|  мм мм
|  мм мм
|  мм мм
| 
| 
| 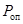 кН кН
|  МПа МПа
| ||||
| I | |||||||||||||||||
| II |
Таблица (продолжение)
| № об | № оп | Расчётные данные | Условия опыта | |||||

| 
| 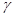
| 
|  МПа
МПа
|  кН
кН
| |||
| I | Осадка на шерохова- тых бойках | |||||||
| II | Осадка на полирован- ных бойках |
3.РАБОТА №3. ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО УГЛА ЗАХВАТА
ПРИ ПРОКАТКЕ
3.1. Общие сведения
Процесс пластической деформации металла между двумя или несколькими вращающимися валками называется прокаткой.

Рис.3. 1. Схема очага деформации при прокатке
Дуга ac на схеме (а также дуга bd) называется дугой захвата или дугой контакта. Соответствующий ей центральный угол  называется углом захвата. Часть прокатываемой полосы, которая подвергается пластической деформации, называется очагом деформации. На схеме область полосы, ограниченная сечениями ab, cd и дугами ас и bd называется геометрическим очагом деформации. Сечение ab образует плоскость входа в очаг деформации, а сечение cd - плоскость выхода из очага деформации. Геометрический очаг деформации является идеализацией. Область полосы, которую занимает реальный или физический очаг деформации больше геометрического очага деформации, и её границы заранее неизвестны.
называется углом захвата. Часть прокатываемой полосы, которая подвергается пластической деформации, называется очагом деформации. На схеме область полосы, ограниченная сечениями ab, cd и дугами ас и bd называется геометрическим очагом деформации. Сечение ab образует плоскость входа в очаг деформации, а сечение cd - плоскость выхода из очага деформации. Геометрический очаг деформации является идеализацией. Область полосы, которую занимает реальный или физический очаг деформации больше геометрического очага деформации, и её границы заранее неизвестны.
При прокатке величина угла захвата не может увеличиваться бесконечно. Пределы, до которых при данном диаметре валков можно увеличивать обжатие  , a следовательно и угол захвата
, a следовательно и угол захвата  , могут быть установлены в результате рассмотрения равновесия системы сил, действующих со стороны валков на прокатываемую полосу в момент её соприкосновения передним торцом с валками. При этом в точке, положение которой определяется величиной угла захвата
, могут быть установлены в результате рассмотрения равновесия системы сил, действующих со стороны валков на прокатываемую полосу в момент её соприкосновения передним торцом с валками. При этом в точке, положение которой определяется величиной угла захвата  , будут действовать две силы: радиальная (нормальная) Р и сила трения (касательная) Т. Обе эти силы могут быть разложены на составляющие Pх, Тх, Ру, Ту по осям X и Y (см. рис.2).
, будут действовать две силы: радиальная (нормальная) Р и сила трения (касательная) Т. Обе эти силы могут быть разложены на составляющие Pх, Тх, Ру, Ту по осям X и Y (см. рис.2).
Составляющие радиальных и касательных сил, направленные по оси Y, будут вызывать обжатие полосы. Составляющие сил по оси X направлены в разные стороны: составляющая Тх силы трения Т будет стремиться втянуть полосу в валки, а составляющая Рx радиальной силы Р - вытолкнуть её из валков.
Очевидно, что соотношение между величинами Pх и Тх будет определять возможность или невозможность осуществления захвата полосы валками. При Tx > Рх захват полосы произойдёт. При Тх= Рх будет иметь место равновесие системы: вращающиеся валки не будут ни втягивать полосу в межвалковое пространство, ни отталкивать её от себя.

Рис. 3.2. Схема сил, действующих на полосу в момент захвата её валками
Запишем уравнения равновесия сил, действующих в направлении оси X [2,5,6]:
2 Тx =2 Рx, или Тх = Рx;
но  ,
,  ;
;
следовательно, можно записать
 .
.
Вспомним, что по закону Кулона радиальная сила Р связана с силой трения Т соотношением
 ,
,
где f - коэффициент трения.
Тогда предыдущее выражение можно записать так

или  , откуда
, откуда  .
.
Поскольку осуществление захвата полосы валками возможно лишь при условии Тх > Рх, то на основании полученных соотношений для этого должно удовлетворяться неравенство 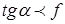 .
.
Тангенс угла (в пределах осуществимых при прокатке углов захвата) приблизительно равен значению его угла, выраженному в радианах. Поэтому можно записать
 <
<  . (3.1)
. (3.1)
При установившемся процессе прокатки, то есть, когда весь очаг деформации заполнен металлом и имеются недеформируемые концы полосы (см. Рис.3.1), можно провести аналогичные рассуждения. Если считать, что нормальные напряжения на контактной поверхности полосы с валками распределены равномерно по дуге захвата, то равнодействующая сила Р переместится к середине длины очага деформации. Точка её приложения будет определяться уже половиной угла захвата  . При этом условии установившийся процесс прокатки становится осуществим при условии
. При этом условии установившийся процесс прокатки становится осуществим при условии
 < f. (3.2)
< f. (3.2)
Таким образом, осуществимость захвата полосы валками и установившегося процесса определяется неравенствами (3.1) и (3.2). Предельными, очевидно, будут соотношения, соответствующие состоянию, при котором Тх = Рх. В этом случае начнётся буксование валков по полосе, то есть валки будут вращаться, а полоса будет неподвижной. При этом углы захвата достигают максимальных значений при данной величине коэффициента трения
 , (3.3)
, (3.3)
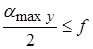 . (3.4)
. (3.4)
Отсюда следует, что  , то есть угол захвата при установившемся процессе меньше угла захвата полосы в начале прокатки в 2 раза.
, то есть угол захвата при установившемся процессе меньше угла захвата полосы в начале прокатки в 2 раза.
В общем виде условия захвата и установившегося процесса можно соответственно записать
 , (3.5)
, (3.5)
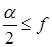 . (3.6)
. (3.6)
Цели работы
1. Определить максимальный угол захвата в момент захвата полосы валками и при установившемся процессе прокатки.
2. Из условий равновесия в момент осуществления захвата полосы валками и установившегося процесса прокатки определить коэффициент внешнего трения.
3. Установить влияние внешнего трения на величину максимального угла захвата.
4.Определить соотношение между максимальным углом захвата в момент захвата (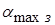 ) и при установившемся процессе прокатки (
) и при установившемся процессе прокатки ( ).
).
Оборудование и инструмент
1.Прокатный стан "130"с валками, имеющими участки с разным состоянием поверхности.
2. Штангенциркуль и масштабная линейка
Образцы из модельного материала
Прямоугольные 20x40x80 мм - 2 шт. и клиновидные с размерами, указанными на рис. 3 - 2 шт.

Рис. 3.3. Клиновидный образец
3.2. Определение максимального угла захвата в момент захвата
Группа студентов разбивается на бригады. Каждой бригаде выдаётся по два прямоугольных образца.
Измерения и ход работы
Сначала предварительно замеряют начальную толщину  обоих выданных прямоугольных образцов. Валки прокатного стана устанавливают так, чтобы зазор между ними составлял примерно 10 мм. Образец кладут на проводковый стол и при помощи деревянного бруска подводят его без нажима передним торцом к вращающимся валкам. Затем, вращая нажимной винт, медленно поднимают верхний валок, увеличивая зазор между валками. В некотором положении верхнего валка произойдёт захват полосы.
обоих выданных прямоугольных образцов. Валки прокатного стана устанавливают так, чтобы зазор между ними составлял примерно 10 мм. Образец кладут на проводковый стол и при помощи деревянного бруска подводят его без нажима передним торцом к вращающимся валкам. Затем, вращая нажимной винт, медленно поднимают верхний валок, увеличивая зазор между валками. В некотором положении верхнего валка произойдёт захват полосы.
Измерив толщину образца  прокатки, определяют величину обжатия
прокатки, определяют величину обжатия
 . Теперь можно рассчитать угол захвата по формуле
. Теперь можно рассчитать угол захвата по формуле
 , (3.7)
, (3.7)
или с помощью приближённой формулы
 , (3.8)
, (3.8)
где D и R – диаметр и радиус валка.
Пользуясь этими выражениями, после подстановки в них опытной величины  , определяют максимальный угол захвата
, определяют максимальный угол захвата  ) в момент захвата. Далее, на основании предельного соотношения (3.3) определяют коэффициент трения f.
) в момент захвата. Далее, на основании предельного соотношения (3.3) определяют коэффициент трения f.
Аналогично поступают и со вторым образцом; только его захват и прокатку осуществляют на той части длины бочки валка, где поверхность имеет большую шероховатость. Таким образом, появляется возможность сравнить максимальные углы захвата  , полученные при разных значениях коэффициента внешнего трения.
, полученные при разных значениях коэффициента внешнего трения.
Опытные и расчётные данные сводят в таблицу.
3.3. Определение максимального угла захвата при установившемся процессе прокатки
На бригаду студентов выдают два клиновидных образца. До прокатки их не замеряют.
Х од работы и измерения
Устанавливают зазор между валками равным 5 мм. Один из образцов задают тонким концом в валки на участке бочки с более чистой поверхностью. Валки будут втягивать клиновидную полосу, обжимая её до толщины  . Поскольку толщина участков клина, поступающих в валки, непрерывно возрастает, также непрерывно растёт и абсолютное обжатие
. Поскольку толщина участков клина, поступающих в валки, непрерывно возрастает, также непрерывно растёт и абсолютное обжатие  .
.
Из выражений (3.7) и (3.8) следует, что с ростом  будет непрерывно возрастать и величина угла захвата
будет непрерывно возрастать и величина угла захвата  . При возрастании a и при данном коэффициенте трения f достигается предельное соотношение (3.4) для установившегося процесса прокатки; валки начнут буксовать по полосе.
. При возрастании a и при данном коэффициенте трения f достигается предельное соотношение (3.4) для установившегося процесса прокатки; валки начнут буксовать по полосе.
В этот момент отключают двигатель стана и с помощью установочного механизма верхний валок поднимают. Остановленную в валках недокатанную полосу извлекают из валков и замеряют  и
и  (рис.3. 4). Затем определяют
(рис.3. 4). Затем определяют
 .
.
Зная  , рассчитывают максимальный угол захвата при установившемся процессе прокатки для данного диаметра валков, используя соотношения (3.7) или (3.8). Используя выражение (3.4), определяют коэффициент трения f.
, рассчитывают максимальный угол захвата при установившемся процессе прокатки для данного диаметра валков, используя соотношения (3.7) или (3.8). Используя выражение (3.4), определяют коэффициент трения f.
Второй клиновидный образец прокатывают на участке длины бочки валка с более шероховатой поверхностью (большее значение f). По достижении при той же, что и в первой половине опыта величине зазора между валками, момента буксования, со вторым образцом поступают точно также как и с первым.
В результате расчёта получают величину  для более высокого значения коэффициента трения f, а по равенству (3.4) и сам коэффициент трения f.
для более высокого значения коэффициента трения f, а по равенству (3.4) и сам коэффициент трения f.

Рис. 3. 4. Клиновидный образец в момент буксования при прокатке
Зная величины f при прокатке первого и второго образцов, можно судить о влиянии коэффициентов внешнего трения на величину максимального угла захвата  при установившемся процессе прокатки.
при установившемся процессе прокатки.
Определив значения  и
и  , необходимо рассчитать отношение
, необходимо рассчитать отношение  и сравнить с теоретически возможным.
и сравнить с теоретически возможным.
Данные, полученные из опыта и рассчитанные, сводят в таблицу.

В отчёте необходимо отметить цели работы, привести эскизы клиновидной полосы до и после прокатки; записать условия осуществления захвата полосы валками и установившегося процесса прокатки. Кратко описать ход работы. На основе полученных данных отчёта сделать вывод о зависимости максимальных углов захвата в момент захвата и при установившемся процессе прокатки от коэффициента внешнего трения, а также о степени отклонений опытных значений  от теоретического.
от теоретического.
4. РАБОТА №4. ЗАВИСИМОСТЬ УШИРЕНИЯ В ГЛАДКИХ ВАЛКАХ ОТ РАЗЛИЧНЫХ ФАКТОРОВ
4.1. Общие сведения
Цель работы. Установление влияния ширины полосы, относительного обжатия, числа проходов (дробности деформации) и состояния контактных поверхностей на уширение металла при прокатке.
При проектировании технологии процесса прокатки необходимо учитывать уширение, т.е. увеличение поперечного размера полосы в процессе деформации её валками. Уширение необходимо знать, для того чтобы выбрать условия прокатки (ритм прокатки, условия трения, размеры валков и т.д.), позволяющие получить из исходной заготовки полосу с заданными размерами поперечного сечения.
Для характеристики уширения используются следующие величины:
1)  - абсолютное уширение, называемое обычно просто “уширением”;
- абсолютное уширение, называемое обычно просто “уширением”;
2)  - коэффициент уширения;
- коэффициент уширения;
3)  - относительный объём, смещённый в ширину (доля металла, смещённого в ширину)
- относительный объём, смещённый в ширину (доля металла, смещённого в ширину)
В этих формулах  и
и 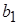 - ширина полосы до прокатки и после неё;
- ширина полосы до прокатки и после неё;  - коэффициент обжатия;
- коэффициент обжатия;  ,
,  - высота полосы до прокатки и после неё.
- высота полосы до прокатки и после неё.
Величина уширения при прокатке на гладкой бочке зависит от условий трения (состояния поверхности валков и полосы, их материала, температуры) и от соотношения геометрических размеров очага деформации. Действительно, силы трения, действующие на поверхности контакта полосы с валками, препятствуют течению металла как в продольном, так и поперечном направлениях, а соотношение между ними, действующими в указанных направлениях, определяют течение металла в ширину. В свою очередь соотношение между поперечными и продольными силами трения зависит от условий трения и соотношения размеров контактной поверхности очага деформации в плане. Кроме того, соотношения геометрических размеров определяют часть поверхности очага деформации, приходящуюся на границу его с внешними (недеформируемыми) зонами. Внешние зоны препятствуют поперечному течению, и уширение будет зависеть от величины поверхности очага деформации с внешними зонами [2,5,6].
Геометрическими характеристиками очага деформации являются диаметр валков D, высота полосы  , ширина её
, ширина её  и длина очага деформации
и длина очага деформации  , которая рассчитывается по формуле
, которая рассчитывается по формуле  (
( - обжатие полосы, R - радиус валков). Таким образом, соотношение между указанными величинами, а также условия трения определяют течение металла при прокатке и, в частности, уширение.
- обжатие полосы, R - радиус валков). Таким образом, соотношение между указанными величинами, а также условия трения определяют течение металла при прокатке и, в частности, уширение.
Известен ряд формул для расчёта величины уширения. Однако в инженерной практике необходимо порой устанавливать влияние различных технологических факторов на уширение, не прибегая к расчётам. В связи с этим в работе ставится задача установить на основании экспериментов качественное влияние различных факторов на уширение. В работе уширение изучается при установившейся стадии прокатки.
4.2. Методика выполнения работ
Работу проводят на стане 130 (диаметр валков 115 мм). Для прокатки используют образцы из модельного материала. Измерения выполняют штангенциркулем.
Работа состоит из четырёх частей.
4.2.1.Зависимость уширения от ширины полосы
Порядок выполнения следующий:
1) на боковых поверхностях клиновидной полосы с переменной шириной (рис.1) проводят вертикальные риски через 10 мм. Риски проводят с таким расчётом, чтобы выделяемый ими объём полосы соответствовал устан