При выполнении чертежей производят различные геометрические построения. Построением называют графический способ решения геометрических задач на плоскости при помощи чертежных инструментов.
Деление окружности на три, шесть и двенадцать равных частей

Рисунок 13. Деление окружности на три, шесть и двенадцать равных частей.
Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности:
- Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью
- Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;
- Точки 1, 2 и 3 делят окружность на три равные части;
- Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;
-Точки 1 - 6 делят окружность на шесть равных частей;
- Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;
- Точки 1 - 12 делят окружность на двенадцать равных частей.
Деление окружности на восемь равных частей

Рисунок 14. Деление окружности на восемь равных частей.
Деление окружности на восемь равных частей производится в следующей последовательности:
Проводят две перпендикулярные оси, которые, пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;
Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.
Деление окружности на пять равных частей

Рисунок 15. Деление окружности на пять равных частей.
Деление окружности на пять равных частей выполняется в следующей последовательности:
- из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
- из точки В опускают перпендикуляр на горизонтальную осевую линию;
- из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;
- из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;
- точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.
Деление окружности на семь равных частей
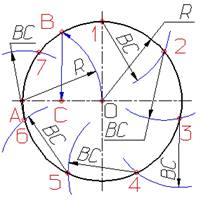
Рисунок 16. Деление окружности на семь равных частей
Деление окружности на семь равных частей выполняется в следующей последовательности:
- из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;
- из точки В опускают перпендикуляр на горизонтальную осевую линию;
- длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7.
Проецирование
Суть метода ортогонального проецирования в следующем: любой предмет можно рассматривать с шести основных точек зрения: спереди, сзади, сверху, снизу, справа и слева. Принято проецировать предмет, находящийся внутри куба, на его грани, при этом предполагается, что зритель находится вне куба, а предмет - за гранью куба, на которую производится проецирование.

Рисунок 17. Проецирование.
После проецирования грани куба как бы разворачиваются и совмещаются в одну плоскость.
Чертеж нескольких проекций пространственного тела (предмета), расположенных на одной линии, называется эпюром.
В черчении изображение обращённой к наблюдателю видимой части поверхности предмета называется видом. Названия видов зависят от того, с какой стороны рассматривают предмет при проецировании.

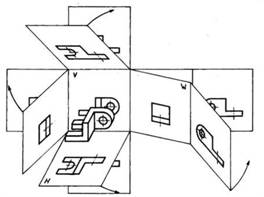
Рисунок 18. Основные виды.
Исходным на чертеже является вид спереди, который называют также главным видом. Если смотреть на предмет слева, под прямым углом к профильной плоскости проекций получают вид слева. Когда смотрят на предмет сверху, перпендикулярно горизонтальной плоскости проекций получают вид сверху.
Направления, по которым смотрят на деталь, получая тот или иной вид, указаны на рис. стрелками с надписями. Каждый вид занимает на чертеже строго определённое место по отношению к главному виду. Вид слева располагают справа от главного вида и на одном уровне с ним, вид сверху - под главным видом. Нельзя нарушать это правило, располагаявиды на произвольных местах без особого обозначения.
Процесс проецирования представлен на рисунке 19:

Рисунок 19. Процесс проецирования.