Красно-черное дерево – это двоичное дерево поиска, вершины которого разделены на красные и черные. Таким образом, каждая вершина хранит один дополнительный код – ее цвет.
При этом должны выполняться определенные требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в 2 раза, поэтому дерево можно назвать сбалансированным.
Каждая вершина красно-черного дерева имеет поля color(цвет), left(левый ребенок), right(правый ребенок) и p(родитель). Если у вершины отсутствует ребенок или родитель, соответствующее поле содержит NIL. Для удобства будем считать, что значения NIL, хранящиеся в полях left и right, являются ссылками на дополнительные листья дерева. В таком пополненном дереве каждая старая вершина имеет двух детей, и тем самым становится внутренней вершиной.
Двоичное дерево поиска называется красно-черным деревом, если оно обладает следующими свойствами(будем считать их RB-свойствами):
1) Каждая вершина – либо красная, либо черная;
2) Каждый лист(NIL) – черный;
3) Если вершина красная оба ее ребенка черные;
4) Все пути, идущие вниз от корня к листьям, содержат одинаковое количество черных вершин.
Рис.1 Красно-черное дерево двоичного поиска
Рассмотрим произвольную вершину х красно-черного дерева и пути, ведущие вниз от нее к листьям. Все они содержат одно и то же число черных вершин. Число черных вершин в любом из них будем называть черной высотой вершины х и обозначать bh(x). Черной высотой дерева будем считать черную высоту его корня.
Следующая лемма показывает, что красно-черные деревья хороши как деревья поиска.
Лемма. Красно-черное дерево с n внутренними вершинами имеет высоту не больше 2log(n+1)
Доказательство. Сначала покажем, что поддерево с корнем в х содержит по меньшей мере 
внутренних вершин. Доказательство проведем индукцией от листьев к корню. Для листьев черная высота равна 0, и поддерево в самом деле содержит не менее 
внутренних вершин. Пусть теперь вершина х не является листом и имеет черную высоту не меньше k – 1. По предположению индукции левое и правое поддеревья вершины х содержат не менее 
вершин, и поэтому поддерево с корнем в х содержит по меньшей мере 
внутренних вершин.
Чтобы завершить доказательство леммы, обозначим высоту дерева через h. Согласно свойству 3, по меньшей мере половину всех вершин на пути от корня к листу, не считая корень, составляют черные вершину. Следовательно, черная высота дерева не меньше h/2. Тогда
.
Перенесем 1 налево и перейдем к логарифмам. Получим
, или 
.
Тем самым для красно-черных деревьев операции Search, Minimum, Maximum, Successor и Predecessor выполняются за время 0(log(n)), так как время их выполнения есть 0(h) для дерева высоты h, а красно-черное дерево с n вершинами имеет высоту 0(log(n)).
Сложнее обстоит дело с процедурами TreeInsert и TreeDelete, проблема в том, что они могут испортить структуру красно-черного дерева, нарушив RB-свойства. Поэтому эти процедуры придется модифицировать.
Вращения
Операции TreeInsert и TreeDelete выполняются на красно-черном дереве за время 0(logn), но они изменяют дерево, и результат может не обладать RB-свойствами. Чтобы восстановить эти свойства надо покрасить некоторые вершины и восстановит структуру дерева.
Рис.2 Операции вращения на двоичном дереве поиска
Мы будем менять структуру с помощью вращений. Вращения представляют собой локальную операцию и сохраняют свойства упорядоченности. На рис.2 показаны два взаимно обратных вращения: левое и правое. Левое вращение возможно в любой вершине х, правый ребенок которой не является NIL. После вращения y оказывается y оказывается сверху, x становится левым ребенком y, а бывший левый ребенок y – правым ребенком x. Процедура RightRotate аналогична.
Процедура LeftRotate:
void tree::LeftRotate(int x){
int y;
y=right[x]; //Находим y.
right[x]=left[y]; //Левое поддерево y становится правым
//поддеревом х.
if(left[y]!=NIL)
{p[left[y]]=x;}
p[y]=p[x]; //Делаем родителя х родителем y
if(p[x]==NIL)
{root=y;}
else{
if(x==left[p[x]])
{left[p[x]]=y;}
else{right[p[x]]=y;}}
left[y]=x; //Делаем х левым ребенком y
p[x]=y;}
void tree::RightRotate(int x){
int y;
y=left[x]; //Находим y.
left[x]=right[y]; //Правое поддерево y становится левым
//поддеревом х.
if(right[y]!=NIL)
{p[right[y]]=x;}
p[y]=p[x]; //Делаем родителя х родителем y
if(p[x]==NIL)
{root=y;}
else{
if(x==left[p[x]])
{left[p[x]]=y;}
else{right[p[x]]=y;}}
right[y]=x; //Делаем х правым ребенком y
p[x]=y;}
Рис.3 Пример действия процедуры LeftRotate.
Добавление вершины
Добавление вершины в красно-черное дерево происходит за время 0(logn). Сначала мы применяем процедуру TreeInsert, как делалось для двоичного дерева поиска, и красим новую Ершину в красный цвет. После этого надо восстановить RB-свойства, для чего приходится перекрасить некоторые вершины и произвести вращения.
void tree::InsertRBTree(int x)
{ cout << "\n";
int y;
left[x]=NIL;right[x]=NIL;
InsertTree(x);
color[x]=RD;
while((x!=root)&(color[p[x]]==RD)){
if(p[x]==left[p[p[x]]]){ // p[x] – левый ребенок
y=right[p[p[x]]];
if(color[y]==RD){
color[p[x]]=BL; //Случай 1
color[y]=BL; //Случай 1
color[p[p[x]]]=RD; //Случай 1
x=p[p[x]];} //Случай 1
else{if(x==right[p[x]]){
x=p[x]; //Случай 2
LeftRotate(x);} //Случай 2
color[p[x]]=BL; //Случай 3
color[p[p[x]]]=RD; //Случай 3
RightRotate(p[p[x]]);}} //Случай 3
else{ // p[x] – правый ребенок
y=left[p[p[x]]];
if(color[y]==RD){
color[p[x]]=BL; //Случай 4-симметричный 1
color[y]=BL; //Случай 4-симметричный 1
color[p[p[x]]]=RD; //Случай 4-симметричный 1
x=p[p[x]];} //Случай 4-симметричный 1
else{if(x==left[p[x]]){
x=p[x]; //Случай 5-симметричный 2
RightRotate(x);} //Случай 5-симметричный 2
color[p[x]]=BL; //Случай 6-симметричный 3
color[p[p[x]]]=RD; //Случай 6-симметричный 3
LeftRotate(p[p[x]]);}}} //Случай 6-симметричный 3
color[root]=BL;}
После выполнения первых трех строк, выполняются все RB-свойства кроме одного: красная вершина х может иметь красного родителя, и это нарушение единственно.
Такая ситуация будет сохраняться после любого числа итераций цикла. После каждой итерации вершина х поднимается вверх по дереву.
Внутри цикла рассматриваются шесть случаев, но три из них симметричны трем другим, различия лишь в том, является ли родитель вершины х левым или правым ребенком своего родителя. Эти случаи разделяются в строке 5.Поэтому мы рассмотри первые 3. Мы будем предполагать, что во всех рассматриваемых нами красно-черных деревьях корень черный, и поддерживать это свойство – для этого используется последняя строка. Поэтому в строке 5 красная вершина не может быть корнем.
Операции внутри цикла начинаются с нахождения вершины y, которая является “дядей” вершины х. Если вершина y красная, имеет место случай 1, если черная – то один из случаев 2 или 3. Во всех случаях вершина p[p[x]] черная, так как пара x - p[x] была единственным нарушением RB-свойств.
Случай 1 показан на рис.5, обе вершины p[x] и y – красные, а вершина p[p[x]] – черная. Перекрасим p[x] и y в черный цвет, а p[p[x]] – в кансый. При этом число черных вершин на любом пути от корня к листьям останется прежним. Нарушение RB-свойств возможно в единственном месте нового дерева: у p[p[x]] может быть красный родитель. Поэтому надо продолжить выполнение цикла, присвоив х значение p[p[x]].
Рис 4. Работа процедуры RB-Insert
Рис. 5 Случай 1
Рис.6 Случаи 2 и 3 в процедуре RBInsert.
В случаях 2 и 3 вершина у черная. Эти два случая различаются тем, каким ребенком х приходится своему родителю – левым или правым. Если правым, исполняется случай 2. В этом случае выполняется левое вращение, которое сводит случай 2 к случаю 3, когда х является левым ребенком. Так как и х и p[x] красные, после вращения количества черных вершин на путях остаются прежними.
Итак, осталось рассмотреть случай 3: красная вершина х является левым ребенком красной вершины p[x], которая является левым ребенком черной вершины p[p[x]], правым ребенком которой является черная вершина у. В этом случае достаточно произвести правое вращение и перекрасить две вершины, чтобы устранить нарушение RB-свойств. Цикл больше не выполняется, так как вершина p[x] теперь черная.
Общее время работы есть O(logn). Причем выполняется не более 2 вращений, после которых мы выходим из цикла.
Удаление вершины
Как и другие операции удаление вершины из красно-черного дерева требует O(logn). Удаление вершины несколько сложнее добавления.
Процедура RBDelete следует схеме процедуры TreeDelete. Вырезав вершину, она вызывает вспомогательную процедуру RBDeleteFixup, которая меняет цвета и производит вращения, чтобы восстановить RB-свойства.
void tree::DeleteRBTree(int z){
int y,x;
if(left[z]==NIL){
y=z;}
else{if(right[z]==NIL){y=z;}
else{y=TreeSuccessor(z);}}
if(left[y]!=NIL)
{x=left[y];
right[x]=right[y];
p[right[x]]=x;}
else{x=right[y];}
p[x]=p[y];
if(p[y]==NIL){
root=x;}
else{if(y==left[p[y]]){
left[p[y]]=x;}
else{right[p[y]]=x;}}
if(y!=z){
if(z==root){root=y;}
if(right[p[z]]==z){
right[p[z]]=y;}else{
left[p[z]]=y;}
p[right[z]]=y;
p[left[z]]=y;
left[y]=left[z];
right[y]=right[z];
p[y]=p[z];
color[y]=color[z];
}
if(color[y]==BL){
DeleteFixup(x);}
При удалении возможны 3 случая если. Если у z нет детей, для удаления z достаточно поместить NIL в соответствующее поле его родителя. Если у z есть один ребенок, можно вырезать z, соединив его родителя напрямую с его ребенком. Если же детей двое, требуются некоторые приготовления: мы находим следующий за z элемент y. Теперь можно скопировать данные из у в z, а из у его ребенку.
Далее если вершина у была черной то ее перемещение могло привести к потер RB-свойств. Для етого необходимо запустить процедуру RBFixup.
Процедура RB-Fixup:
void tree::DeleteFixup(int x){
int w;
while((x!=root)&(color[x]==BL)){
if(x==left[p[x]]){
w=right[p[x]];
if(color[w]==RD){
color[w]=BL; //Случай 1
color[p[x]]=RD; //Случай 1
LeftRotate(p[x]); //Случай 1
w=right[p[x]];} //Случай 1
if((color[left[w]]==BL)&(color[right[w]]==BL)){
color[w]=RD; //Случай 2
x=p[x];} //Случай 2
else{if(color[right[w]]==BL)
{color[left[w]]=BL; //Случай 3
color[w]=RD; //Случай 3
RightRotate(w); //Случай 3
w=right[p[x]];} //Случай 3
color[w]=color[p[x]]; //Случай 4
color[p[x]]=BL; //Случай 4
color[right[w]]=BL; //Случай 4
LeftRotate(p[x]); //Случай 4
x=root;}} //Случай 4
else{
w=left[p[x]];
if(color[w]==RD){ //Случай симметричный 1
color[w]=BL; //Случай симметричный 1
color[p[x]]=RD; //Случай симметричный 1
RightRotate(p[x]); //Случай симметричный 1
w=left[p[x]];}
if((color[right[w]]==BL)&(color[left[w]]==BL)){
color[w]=RD; //Случай симметричный 2
x=p[x];} //Случай симметричный 2
else{if(color[left[w]]==BL)
{color[right[w]]=BL; //Случай симметричный 3
color[w]=RD; //Случай симметричный 3
LeftRotate(w); //Случай симметричный 3
w=left[p[x]];} //Случай симметричный 3
color[w]=color[p[x]]; //Случай симметричный 4
color[p[x]]=BL; //Случай симметричный 4
color[left[w]]=BL; //Случай симметричный 4
RightRotate(p[x]); //Случай симметричный 4
x=root;}}} //Случай симметричный 4
color[x]=BL;} 
Рис. 7 Случай 1 и 2 в процедуре RB-Fixup
Рис. 8 Случай 3 и 4 в процедуре RB-Fixup
Передаваемая процедуре вершина х это вершина являющаяся ребенком у. Если удаленная процедурой RBTreeDelete вершина была черной, то любой путь, через нее проходивший, теперь содержит на одну черную вершину меньше. Таким образом, свойство 4 нарушилось. Мы можем компенсировать это а счет вершины х, занявшей место вершины у. Если х – красная, сделаем ее черной. Если х – черная, объявим ее дважды черной и будем считать за две при подсчете числа черных вершин на пути от корня к листьям. Конечно, такой выход может быть лишь временным, поскольку определение красно-черных деревьев не предусматривает дважды черных вершин, и мы должны постепенно избавиться от такой вершины.
Процедура RB-Fixup применяется к дереву, которое обладает свойствами красно-черного дерева, если учесть дополнительную единицу черноты в вершине х, и превращает его в настоящее красно-черное дерево. В цикле дерево меняется, и значение переменной х тоже меняется, но сформулированное свойство остается верным.
Цикл завершается, если (1) х указывает на красную вершину, тогда мы красим ее в черный цвет, или если (2) х указывает на корень, тогда лишняя чернота может быть просто удалена. Может оказаться также, что (3) внутри тела цикла удается выполнить несколько вращений и перекрасить несколько вершин, после чего дважды черная вершина исчезнет. В этом случае присваивание х=root позволяет выйти из цикла.
Внутри цикла х указывает на дважды черную вершину, не являющуюся корнем. В строке 3 мы определяем, каким ребенком является х – левым или правым. Подробно описана часть процедуры для случая с левым ребенком, второй случай симметричен. Переменная w (строка 4) указывает на вторго ребенка вершины p[x]. Так как вершина х – дважды черная, w не может быть равно NIL, поскольку в это случае вдоль одного пути от p[x] вниз было бы меньше черных вершин, чем вдоль другого.
Четыре возможных случая показаны на рис. 7 и рис. 8. Прежде чем разбираться с ними детально, посмотрим, как проверить, что преобразования не нарушают свойство 4. Достаточно убедиться, что количество черных вершин от корня показанного поддерева до каждого из поддеревьев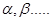 
не изменилось. Например на рисунке иллюстрирующим первый случай, количество черных вершин от корня до каждого из поддеревьев 
равно 3 как до, так и после преобразования. Аналогично, количество черных вершин от корня до 
равно 2 до и после преобразования. На рисунке, иллюстрирующим 2 случай, вершина B может быть и черной, и красной. Если она красная, то число черных вершин от корня до 
равно 2, если черная то 3. Остальные случаи проверяются аналогично.
Итак, рассмотрим все случаи по порядку. Случай 1 имеет место, когда вершина w, брат х, красная. Так как оба ребенка вершины w черные, мы можем поменять цвета w и p[x] и произвести левое вращение вокруг p[x], не нарушая RB-свойств. Вершина х остается дважды черной, а ее новый брат – черный, так что мы свели дело к одному из случаев 2, 3 или 4.
Если вершина w черная, имеет место один из случаев 2-4. Они различаются между собой цветом детей вершины w. В случае 2 оба ребенка вершины w черные. Так как вершина w тоже черная, мы можем снять черную окраску с х и с w, и добавить черноту родителю, p[x]. После этого продолжим выполнение цикла. Заметим, что если мы попали в случай 2 из случая 1, то вершина p[x] – красная, поэтому цикл сразу же завершится.
В случае 3 вершина w черная, ее левый ребенок – красный, а правый – черный. Мы можем поменять цвета w и ее левого ребенка и потом применить правое вращение так, что RB-свойства будут сохранены. Новым братом вершины х теперь будет черная вершина с красным правым ребенком, и мы свели случай 3 к случаю 4.
Наконец, в случае 4 вершина w является черной, а ее правый ребенок красный. Меняя некоторые цвета и производя левое вращение вокруг p[x], мы можем удалить лишнюю черноту у х, не нарушив RB-свойств. Присваивание х=root выводит нас из цикла.
Таким образом, процедура RBFixupDelete требует времени O(logn), и общее время RBDelete также есть O(logn), отметим, что при это производится не более 3 вращений.
Заключение
В курсовой работе были рассмотрены двоичные деревья поиска. Более подробно были рассмотрены красно-черные деревья. Которые более подходят для процедуры поиска так как являются сбалансированными. Время выполнения операций не более O(logn).