Лекция 6.1 Параметрические методы сравнения 2х независимых совокупностей данных
Общее в сравнении 2х независимых совокупностей данных
В таблице приводятся 7 различных критериев (методов) сравнения 2х независимых совокупностей. Выбор метода зависит от уровня измерения анализируемой переменной. При этом, методы, предлагаемые для номинальных переменных можно использовать и для порядковых и метрических. Методы, предлагаемые для порядковых, применимы и для метрических, но не применимы для номинальных переменных. Методы, предлагаемые для метрических переменных, применимы только для этого уровня измерения (не применимы для порядковых и номинальных).

Следует также иметь ввиду, что эти критерии не всегда являются аналогами с точки зрения выводов. В таблице ниже приводится информация о том, какие выводы можно сделать применив тот или иной метод (методы, которые являются аналогами по отношению к друг другу выделены одним цветом поля).

СРАВНЕНИЕ ДИСПЕРСИЙ ДВУХ НЕЗАВИСИМЫХ СОВОКУМНОСТЕЙ ДАННЫХ
Основными условиями для использования критерия Фишера при сравнении дисперсий двух совокупностей являются: (1) метрический уровень измерения переменной и (2) соответствие выборочных данных нормальному закону распределения.
Сравнение дисперсий позволяет оценить различие в вариативности признака в выборках. Чаще всего такая задача в психологических исследованиях не ставится как самостоятельная, а рассматривается как промежуточный этап при решении других статистических задач, зависящих от равенства дисперсий. Например, при сравнении средних t критерием Стьюдента.

Сглаженные графики распределения относительных частот (долей) для юношей и девушек по показателю тревожности. График 1 – юноши, график 2 - девушки (Наследов А.Д., 2007).
Сравнивая графики на рисунке, можно сделать выводы как по уровню выраженности, так и по индивидуальной изменчивости тревожности у юношей и девушек. Так, юноши в среднем менее тревожны, чем девушки. Но изменчивость по тревожности выше у юношей, чем у девушек: девушки в этом отношении более похожи друг на друга (Наследов А.Д., 2007).
Для оценки равенства дисперсий используют дисперсионное отношение Фишера (Гласс Дж., Стэнли Дж., 1976; стр.179):

Статистические гипотезы:
1. Нулевая гипотеза Н0: генеральные дисперсии равны.
2. Альтернативная гипотеза Н1: генеральные дисперсии различны.
Если Fэмп > Fкрит, то нулевую гипотезу Н0 отвергают на соответствующем уровне значимости и принимают альтернативную гипотезу
Пример сравнения дисперсий
Задача: Отличаются ли две учебные группы психологов по вариативности тревожности?
Для проверки гипотезы были сравнены дисперсии двух учебных групп психологов (женщины). Испытуемым был предложен опросник MMPI. В примере приводится анализ по шкале Pt7 этого опросника – шкала психастении / тревожности (кол-во баллов). Данные по шкале и необходимые предварительные вычисления приведены в таблице ниже:
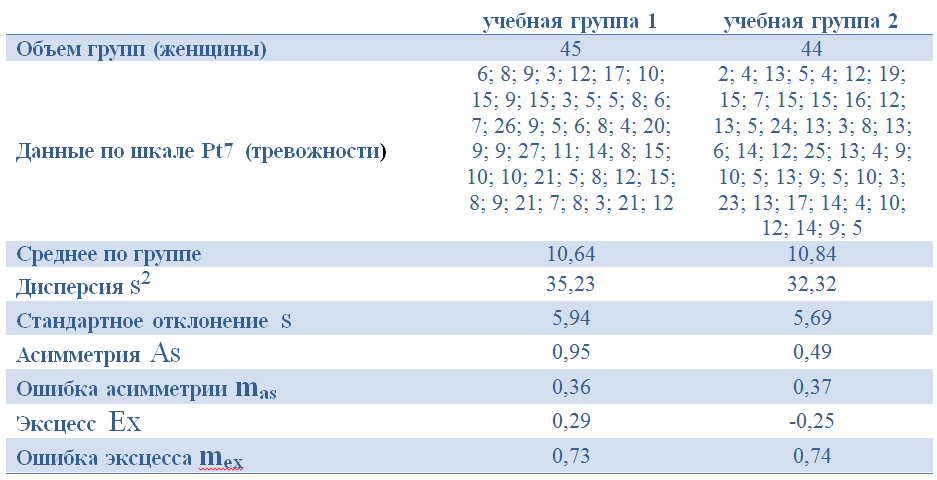
Решение
Этап 1: проверка на соответствие выборочных данных нормальному закону распределения
Проведем проверку посредством оценки асимметрии и эксцесса. Выборочные данные соответствуют нормальному закону в том случае, если асимметрия и эксцесс незначительны.
Схема проверки выраженности асимметрии
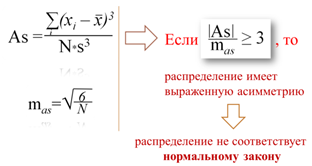

| В учебной группе №1 = 0,95/0,36 = 2,61 < 3 соответствует закону нормального распределения | В учебной группе №2 = 0,49/0,37 = 1,33 < 3 соответствует закону нормального распределения |