Проведем проверку через оценку выраженности асимметрии и эксцесса. Выборочные данные соответствуют нормальному закону в том случае, если асимметрия и эксцесс незначительны.

| В медитативной группе = 0,36/0,53 = 0,68 < 3 соответствует закону нормального распределения | В контрольной группе = 0,18/0,56 = 0,32 < 3 соответствует закону нормального распределения |

| В медитативной группе = 1,35/1,07 = 1,26 < 3 соответствует закону нормального распределения | В контрольной группе = 1,16/1,12 = 1,04 < 3 соответствует закону нормального распределения |
Пример2 шаг 2 равенство дисперсий
Общий вывод по первому этапу: выборочные данные соответствуют закону нормального распределения. Таким образом, переходим ко второму этапу - проверке гипотезы о равенстве дисперсий.

Этап 2: проверка равенства дисперсий

Статистика F как отношение двух дисперсий. В числителе – большая дисперсия из двух.
Эмпирическое значение F(18;20) = 125,61/92,03 = 1,36
По таблице Фишера (приложение 4) находим критические значения для уровней значимости 0,05 и 0,01
Критическое значение F(18;20)0,05 = 2,15
Критическое значение F(18;20)0,01 = 3,01

Пример шаг 3 сравнения средних
вывод: так как эмпирическое значение F попадает в область допустимых отклонений, то принимаем нулевую гипотезу о равенстве дисперсий
Этап 3: проверка равенства средних значений
1. Нулевая гипотеза Н0: Среднее значение по шкале I опросника POI в «медитативной» группе не отличается от среднего в контрольной
2. Альтернативная гипотеза Н1 (направленная): Среднее значение по шкале I опросника POI в «медитативной» группе больше среднего в контрольной.
Поскольку мы приняли гипотезу о равенстве дисперсий, то вычисление эмпирического значения Стьюдента надо производить по следующей формуле:

Мы уже рассчитали среднее значение и дисперсию в каждой группе

Вычислим обобщенную дисперсию, подставляя значения из таблицы → s2 = 107,93 → стандартное отклонение s = 10,39
Эмпирическое значение статистики Стьюдента t = 2,405, Степени свободы k = 38 (df=38)
Пример 2 шаг 3 сравнение средних оценка значимости
Для односторонней критической области в таблице значений Стьюдента (приложение, таблица 2) находим критические значения:
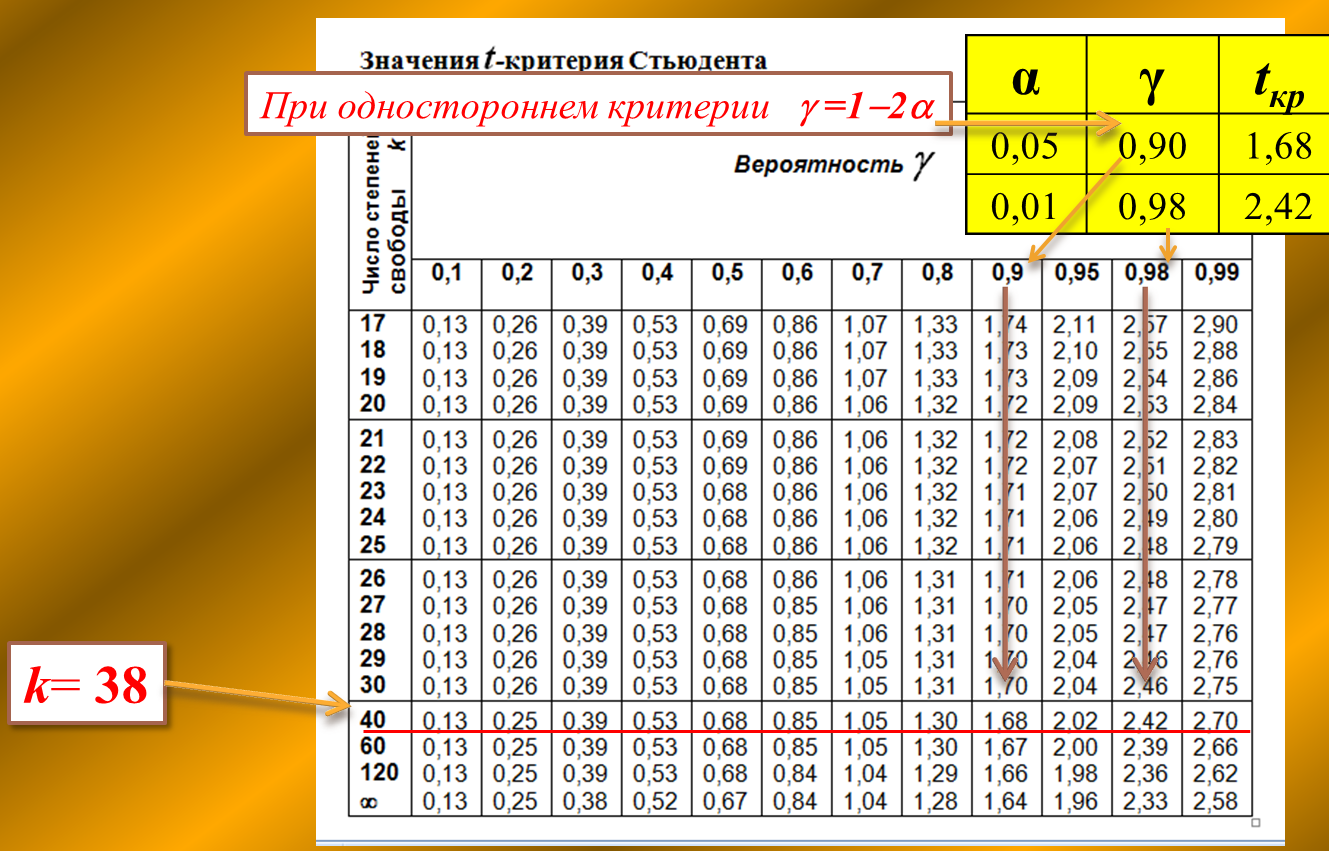
| Вероятность α | Вероятность γ | Критическое значение t |
| 0.05 → | 0.90 → | 1.68 |
| 0.01 → | 0.98 → | 2.42 |

Вывод: так как эмпирическое значение t превышает критическое, то отвергаем нулевую гипотезу на уровне значимости 0,05 и принимаем альтернативную о том, что среднее значение по шкале I опросника POI в «медитативной» группе больше среднего в контрольной
SPSS равенство дисперсий и средних
Для того, чтобы провести оценку равенства дисперсий и средних в приложении SPSS, надо в меню "Анализ" перейти на "сравнение средних" (compare means) и далее на "Т-критерий для независимых выборок" (independent-samples test)

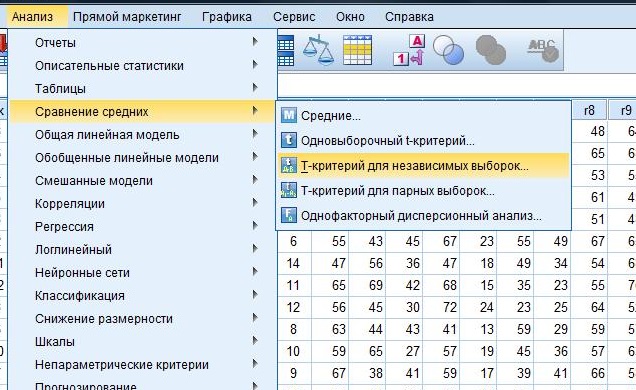
SPSS шаг 2
Во всплывающем окне перебросить в первый лист (проверяемые переменные) переменные, которые вы собираетесь сравнивать по средним и дисперсиям. Во строку ниже (группировать по) нужно перебросить переменную, которая классифицирует испытуемых по группам.

С этой строке необходимо указать коды по которым классифицируются испытуемые на группы
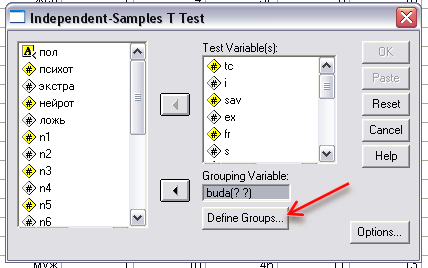
Например, 1 - экспериментальная группа и 0 – контрольная

SPSS шаг 3 результат
После чего нажимаете OK и получаете отчет. Отчет содержит две таблицы. Первая содержит описательную информацию о группах (количество наблюдений, средние, стандартные отклонения).

Вторая таблица содержит результат сравнения групп по дисперсиям и средним.



Следует заметить, что для каждой переменной дается по два значения t, df, sig. (две строки). Выбор верхней или нижней строки данных определяется выводами сравнения дисперсий. Если принята гипотеза о равенстве дисперсий, то используется верхняя строка в статистики Стьюдента (Equal variances assumed). Если принята гипотеза о неравенстве дисперсий (в третьем столбце значение sig<0,05), то используется нижняя строка в статистики Стьюдента (Equal variances not assumed).
В русскоязычной версии:

Если дисперсии равны, как для переменной "Продуктивность", то при сравнении средних мы используем первую строку.

В данном примере мы считаем, что средние равны, потому что значение значимости (=0,531) не меньше 0,05.
В этом примере и дисперсии неравны и средние неравны.
Поскольку дисперсии неравны мы используем для оценки значимости равенства средних вторую строку
