Приведём другое решение. Прямоугольный треугольник

Прямоугольный треугольник

Задание 16 № 118

В тре­уголь­ни­ке ABC угол C прямой, BC = 8, sin A = 0,4. Найдите AB.

Решение.

Синус угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та ВС к ги­по­те­ну­зе АВ. Поэтому:

 

Ответ: 20.

Ответ: 20

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.

Задание 16 № 132773

Два ост­рых угла пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4:5. Най­ди­те боль­ший ост­рый угол. Ответ дайте в градусах.

Решение.

Сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90°. Ост­рые углы пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4 части к 5 частям, сумма этих углов 4 + 5 = 9 частей. По­это­му одна часть равна 10°. Так как боль­ший угол со­дер­жит в себе 5 частей, он равен 5·10° = 50°.

 

Ответ: 50.

Ответ: 50

Задание 16 № 311387

В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

Решение.

Так как тре­уголь­ник ABC — прямоугольный, то . Имеем:

 

 

Ответ: 21.

Ответ: 21

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

Задание 16 № 311399

В тре­уголь­ни­ке угол равен 90°, . Найдите .

Решение.

Так как тре­уголь­ник ABC — прямоугольный, то . Имеем:

 

 

Ответ: 33.

Ответ: 33

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)

Задание 16 № 311498

В тре­уголь­ни­ке угол прямой, . Най­ди­те .

Решение.

Треугольник ABC — прямоугольный. Таким образом,

 

 

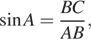
Ответ: 20.

Ответ: 20

Источник: ГИА-2013. Математика. Экзамен. Вариант 9

Задание 16 № 311500

В тре­уголь­ни­ке угол прямой, . Най­ди­те .

Решение.

Треугольник ABC — прямоугольный. Таким образом,

 

 

Ответ: 30.

Ответ: 30

Источник: ГИА-2013. Математика. Экзамен. Вариант 10

Задание 16 № 311760

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 20, tg A = 0,5. Най­ди­те BC.

Решение.

Тангенс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та к прилежащему, поэтому

 

 

 

Ответ: 10.

Ответ: 10

Задание 16 № 311816

В тре­уголь­ни­ке ABC угол C равен 90°, BC = 20, = 0,5. Най­ди­те AC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му:

 

 

Ответ: 40.

Ответ: 40

Задание 16 № 316283

В тре­уголь­ни­ке ABC угол C равен 90°, BC = 12, tg A = 1,5. Най­ди­те AC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му:

 

 

Ответ: 8.

Ответ: 8

Задание 16 № 316320

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 12, tg A = 1,5. Най­ди­те BC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му поэтому:

 

Ответ: 18.

Ответ: 18

Задание 16 № 322819

Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны 35 и 120. Най­ди­те вы­со­ту, про­ве­ден­ную к ги­по­те­ну­зе.

Решение.

Пусть ка­те­ты имеют длины и а ги­по­те­ну­за — длину Пусть длина высоты, проведённой к ги­по­те­ну­зе равна Найдём длину ги­по­те­ну­зы по тео­ре­ме Пифагора:

 

 

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка может быть най­де­на как по­ло­ви­на про­из­ве­де­ния ка­те­тов или как по­ло­ви­на про­из­ве­де­ния высоты, проведённой к ги­по­те­ну­зе на гипотенузу:

 

 

Ответ: 33,6.

Ответ: 33,6

33,6

Задание 16 № 322979

Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны и 1. Най­ди­те синус наи­мень­ше­го угла этого тре­уголь­ни­ка.

Решение.

Пусть ка­те­ты имеют длины и а ги­по­те­ну­за — длину Найдём длину ги­по­те­ну­зы по тео­ре­ме Пифагора:

 

 

Наименьший угол в тре­уголь­ни­ке лежит про­тив наи­мень­шей стороны, 4 > 1 следовательно, синус наи­мень­ше­го угла равен:

Ответ: 0,25.

Ответ: 0,25

0,25

Задание 16 № 323344

Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину ги­по­те­ну­зы.

Решение.

Пусть — длина катета, лежащего против угла в 30°, тогда гипотенуза равна второй катет равен .

Площадь прямоугольного треугольника равна половине произведения катетов.

 

 

Следовательно, длина гипотенузы, равна 16.

 

Ответ: 16.

 

Приведём другое решение.

 

Пусть длина ги­по­те­ну­зы равна а длина катета, при­ле­жа­ще­го к углу 30° равна Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

 

 

Откуда получаем:

 

Ответ: 16

Задание 16 № 339365

В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Решение.

По опре­де­ле­нию тан­ген­са от­ку­да По тео­ре­ме Пифагора:

 

 

Ответ: 28.

Ответ: 28

Задание 16 № 339370

В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Решение.

Найдём ко­си­нус угла

 

 

По опре­де­ле­нию косинуса, от­ку­да

Ответ: 15

Задание 16 № 339385

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину катета, ле­жа­ще­го на­про­тив этого угла.

Решение.

Пусть длина ги­по­те­ну­зы равна а длина катета, ле­жа­ще­го на­про­тив угла 30° равна Сумма углов в тре­уголь­ни­ке равна 180°, следовательно, вто­рой ост­рый угол равен 180° − 90° − 30° = 60°. Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

 

 

Откуда получаем:

 

 

Ответ: 38.

Ответ: 38

Задание 16 № 339406

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину катета, при­ле­жа­ще­го к этому углу.

Решение.

Пусть длина ги­по­те­ну­зы равна а длина катета, при­ле­жа­ще­го к углу 30° равна Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

 

 

Откуда получаем:

 

 

Ответ: 34.

Ответ: 34

Задание 16 № 339436

Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 6, AC = 24.

Решение.

Рассмотрим тре­уголь­ни­ки и они — прямоугольные, угол — общий, следовательно, тре­уголь­ни­ки подобны. Откуда:

 

Ответ: 12.

Ответ: 12

Источник: Банк заданий ФИПИ

Задание 16 № 340000

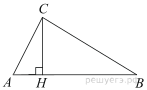
В пря­мо­уголь­ном тре­уголь­ни­ке катет , а вы­со­та , опу­щен­ная на гипотенузу, равна Най­ди­те

Решение.

Из пря­мо­уголь­но­го тре­уголь­ни­ка по тео­ре­ме Пи­фа­го­ра найдём

 

 

Углы и равны как углы с вза­им­но пер­пен­ди­ку­ляр­ны­ми сторонами, по­это­му их си­ну­сы равны:

 

Ответ: 0,2.

Ответ: 0,2

0,2

Задание 16 № 340078

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 4, tg A = 0,75. Най­ди­те BC.

Решение.

По опре­де­ле­нию тангенса:

Ответ: 3.

Ответ: 3

Задание 16 № 340384

В тре­уголь­ни­ке = 35, угол равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 20.

Ответ: 20

Задание 16 № 341380

Найдите пло­щадь пря­мо­уголь­но­го треугольника, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 12 и 13.

Решение.

По тео­ре­ме Пифагора най­дем второй катет: , зна­чит, площадь равна:

 

 

Ответ: 30.

Ответ: 30

Задание 16 № 348415

Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов () равна квадрату гипотенузы (). Таким образом:

 

 

 

Ответ: 17

Ответ: 17

Задание 16 № 348419

В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов () равна квадрату гипотенузы (). Таким образом:

 

 

 

Ответ: 9

Ответ: 9

Задание 16 № 348430

В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов () равна квадрату гипотенузы (). Таким образом:

 

 

 

Ответ: 30

Ответ: 30

Задание 16 № 348615

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 10.

Ответ: 10

Задание 16 № 348758

Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Ответ: 67

Ответ: 67

Задание 16 № 348837

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 9,5.

Ответ: 9,5

9,5

Задание 16 № 348945

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 15,5.

Ответ: 15,5

15,5

Задание 16 № 348999

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 22.

Ответ: 22

Задание 16 № 349009

В треугольнике угол равен 90°, , . Найдите .

Решение.

Синус угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та ВС к ги­по­те­ну­зе АВ. Поэтому:

 

Ответ: 2.

Ответ: 2

Задание 16 № 349061

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 18.

Ответ: 18

Задание 16 № 349073

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

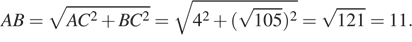
Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 5,5.

Ответ: 5,5

5,5

Задание 16 № 349084

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 10.

Ответ: 10

Задание 16 № 349181

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 6

Ответ: 6

Задание 16 № 349193

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 20

Ответ: 20

Задание 16 № 349195

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 12

Ответ: 12

Задание 16 № 349225

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 4.

Ответ: 4

Задание 16 № 349294

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

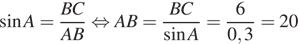
Ответ: 20

Ответ: 20

Задание 16 № 349357

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 8

Ответ: 8

Задание 16 № 349434

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 2,5.

Ответ: 2,5

2,5

Задание 16 № 349483

Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Ответ: 69

Ответ: 69

Задание 16 № 349485

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 5.

Ответ: 5

Задание 16 № 349522

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 19.

Ответ: 19

Задание 16 № 349526

Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Ответ: 47

Ответ: 47

Задание 16 № 349534

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 21,5.

Ответ: 21,5

21,5

Задание 16 № 349585

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 5

Ответ: 5

Задание 16 № 349686

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 5.

Ответ: 5

Задание 16 № 349694

Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Ответ: 27

Ответ: 27

Задание 16 № 349799

В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы . Таким образом,

 

 

Ответ: 12

Ответ: 12

Задание 16 № 349840

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

 

 

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

 

Ответ: 14.

Ответ: 14

Задание 16 № 349868

Два катета прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

Решение.

По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы . Таким образом,

 

 

Ответ: 34

Ответ: 34

Задание 16 № 349873

Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Ответ: 33

Ответ: 33

Задание 16 № 350007

В треугольнике угол равен 90°, , . Найдите .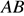

Решение.

В прямоугольном треугольнике синус угла - отношение противолежащего катета к гипотенузе, следовательно:

 

 

Ответ: 4

Ответ: 4

Задание 16 № 353514

Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 8, AC = 32.