Лекция 2_Корреляционный и регрессионный анализ
План:
1. Корреляционная зависимость
2. Линейная парная регрессия
3. Коэффициент корреляции
Корреляционная зависимость
Под функциональной зависимостью понимают такую зависимость, когда каждому значению одной переменной соответствует вполне определенное значение другой.
В экономике в большинстве случаев между переменными величинами существуют зависимости, при которых каждому значению одной переменной соответствует не какое-то определенное значение, а множество возможных значений другой переменной.
Определение. Зависимость называется статистической, если каждому значению одной переменной соответствует определенное (условное) распределение другой переменной.
Примером статистической связи может служить зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности.
Частным случаем статистической зависимости является такая зависимость, при которой изменению одной величины соответствует изменение среднего значения (математического ожидания) другой величины.
Определение. Статистическая зависимость между двумя переменными, при которой каждому значению одной переменной соответствует определенное среднее значение (условное математическое ожидание) другой, называется корреляционной.
Другими словами, корреляционная зависимость между двумя переменными – это функциональная зависимость между значениями одной из них и условным математическим ожиданием другой величины:
 (11.1)
(11.1)
Наиболее общей является статистическая зависимость, ее частным случаем является корреляционная зависимость. Частным случаем корреляционной является функциональная зависимость.
Уравнения (11.1) называются модельными уравнениями регрессии или просто уравнениями регрессии соответственно У по Х и Х по У. Правые части уравнений (11.1) называют функциями регрессии, а их графики – линиями регрессии.
Цель регрессионного анализа - оценка функциональной зависимости условного среднего значения результативного признака от факторных х₁, х₂,… хn в виде уравнения регрессии ŷ = f(х₁, х₂,… хn).
Число факторных признаков, включаемых в модель, должно быть оптимально и должно быть в 5-6 раз меньше объема изучаемой совокупности.

Линейная парная регрессия
Даны наблюдения 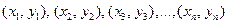 .
.
Пусть зависимость результирующего признака у от факторного признака х будем искать в виде линейной зависимости:
 . (11.2)
. (11.2)
Применяем метод наименьших квадратов (МНК). Согласно этому методу неизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi, где i=1, 2,…,n, от значений yxi, найденных по уравнению регрессии(11.2), была минимальной:
 (11.3)
(11.3)
На основании необходимого условия экстремума функции двух переменных приравниваем к нулю частные производные функции 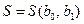 .
.
То есть для нахождения параметров необходимо решить систему:
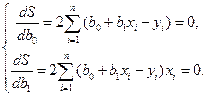 (11.4)
(11.4)
После преобразований системы (11.4) получим:
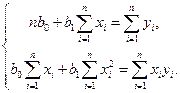 (11.5)
(11.5)
Решая систему линейных уравнений (11.5), получим параметры уравнения линейной регрессии (11.2).
В уравнении линейной регрессии (11.2) параметр b0 – свободный член регрессии. Отражает влияние неучтенных факторов на результирующий признак у.
Параметр b1 называется коэффициентом регрессии, который показывает на сколько единиц изменяется переменная у при изменении х на одну единицу. Если b1>0, то связь между х и у прямая, если b1<0, то связь обратная.
Ошибка аппроксимации для каждого наблюдения определяется по формуле:
 .
.
Средняя ошибка аппроксимации находится как средняя арифметическая из индивидуальных ошибок.
Коэффициент корреляции
Тесноту линейной связи оценивают выборочным коэффициентом корреляции r.
Коэффициент корреляции r совпадает по знаку с коэффициентом регрессии. Если  , то корреляционная связь между переменными называется прямой, если
, то корреляционная связь между переменными называется прямой, если  - обратной. При прямой (обратной) связи увеличение одной из переменных ведёт увеличению (уменьшению) условной средней другой.
- обратной. При прямой (обратной) связи увеличение одной из переменных ведёт увеличению (уменьшению) условной средней другой.
Коэффициент корреляции находится по формуле:
 (11.6)
(11.6)
где 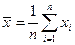 ,
, 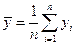 ,
, 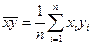 ,
, 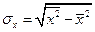 ,
, 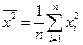 ,
, 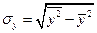 ,
, 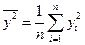 .
.
Отметим основные свойства коэффициента корреляции:
1. Коэффициент корреляции принимает значения на отрезке  , т.е.
, т.е.
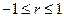 .
.
В зависимости от того, насколько  приближается к 1, различают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную, т.е. чем ближе
приближается к 1, различают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную, т.е. чем ближе  к 1, тем теснее связь.
к 1, тем теснее связь.
2. Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, то величина коэффициента корреляции не изменится.
3.При 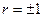 корреляционная связь представляет линейную функциональную зависимость. При этом линии регрессии Y по Х и Х по Y совпадают и все наблюдаемые значения располагаются на общей прямой.
корреляционная связь представляет линейную функциональную зависимость. При этом линии регрессии Y по Х и Х по Y совпадают и все наблюдаемые значения располагаются на общей прямой.
4. При r = 0 линейная корреляционная связь отсутствует.

Коэффициент детерминации определяется по формуле  и показывает на сколько процентов вариация у объясняется вариацией х.
и показывает на сколько процентов вариация у объясняется вариацией х.
Значимость уравнения регрессии проверяют с помощью критерия Фишера  , где n – число наблюдений.
, где n – число наблюдений.
Если расчетное значение F больше табличного F(α; k1; k2), то уравнение регрессии статистически значимо. Где k1 для парной регрессии равно 1, k2 равно числу наблюдений минус количество оцениваемых коэффициентов (для парной регрессии (n-2)), α – уровень значимости.