(рис.2)
В этом методе положение тела на траектории его движения задается радиусом-вектором r, проведенным из произвольной точки О, называемой полюсом, в заданную точку траектории. Точка О обязательно должна быть связана с выбранным материальным телом, называемым телом отсчета. Вектор  , проведенный из точки
, проведенный из точки  в точку
в точку  положения тела на траектории (рис.2) называется перемещением тела. Точки нумеруются в порядке возрастания времени движения тела. Длина
положения тела на траектории (рис.2) называется перемещением тела. Точки нумеруются в порядке возрастания времени движения тела. Длина  участка траектории между этими точками называется длиной пути тела или путем, пройденным телом, между этими точками.
участка траектории между этими точками называется длиной пути тела или путем, пройденным телом, между этими точками.
Скорость  и ускорение a тела определяются как
и ускорение a тела определяются как
 ,
,  .
.
Вектор скорости  всегда направлен по касательной к траектории движения тела, в направлении его импульса
всегда направлен по касательной к траектории движения тела, в направлении его импульса  , а вектор ускорения a, согласно второму закону Ньютона, – в направлении результирующей силы
, а вектор ускорения a, согласно второму закону Ньютона, – в направлении результирующей силы  , действующей на тело. Направления векторов F и p, а значит и векторов a и v при движении тела по криволинейной траектории не совпадают.
, действующей на тело. Направления векторов F и p, а значит и векторов a и v при движении тела по криволинейной траектории не совпадают.
Изменение скорости  тела и его перемещение
тела и его перемещение  за время t его движения определяются соотношениями
за время t его движения определяются соотношениями
 ,
,  ,
,
где  и
и  – начальная скорость и начальное положение тела при
– начальная скорость и начальное положение тела при 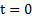 .
.
При движении тела с постоянным ускорением  уравнения движения тела будут иметь вид
уравнения движения тела будут иметь вид

Пример 1. См. пример 4.5.
Координатный метод описания движения тела. В этом методе для описания движения тела обычно выбирается декартова (прямоугольная) система координат XYZ с началом в произвольной точке О, связанной с телом отсчета. Такая система координат называется лабораторной системой отсчета. Возможно также использование других систем координат: полярной, цилиндрической, сферической и т.д. Направления координатных осей X,Y,Z выбираются произвольно, но рационально, чтобы решение задачи оказалось максимально простым.
В декартовой системе координат положение тела на его траектории относительно начала О выбранной системы отсчета задается уравнением  , где (x, y, z) – координаты положения материальной точки или центра масс (ЦМ) тела, а i, j, k –орты (единичные векторы) координатных осей X, Y, Z (рис.2). Скорость тела по определению равна
, где (x, y, z) – координаты положения материальной точки или центра масс (ЦМ) тела, а i, j, k –орты (единичные векторы) координатных осей X, Y, Z (рис.2). Скорость тела по определению равна

где  – компоненты вектора скорости
– компоненты вектора скорости  тела в направлении осей X, Y, Z (проекции вектора
тела в направлении осей X, Y, Z (проекции вектора  на оси X, Y,Z).
на оси X, Y,Z).
Ускорение тела по его определению
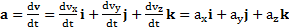 ,
,
где  – компоненты вектора ускорения a тела в направлении осей X, Y, Z (проекции вектора a на оси X, Y, Z).
– компоненты вектора ускорения a тела в направлении осей X, Y, Z (проекции вектора a на оси X, Y, Z).
Величины скорости и ускорения тела равны
 ,
,  .
.
В случае двумерного движения тела (z=0) ориентации векторов  и a по отношению к оси X определяются соотношениями
и a по отношению к оси X определяются соотношениями
 .
.
В случае плоского движения изменения скорости тела  и
и  и его перемещения
и его перемещения  и
и  вдоль осей X и Y равны
вдоль осей X и Y равны


где  и
и  – компоненты начальной скорости и координаты начального положения тела вдоль осей X и Y при
– компоненты начальной скорости и координаты начального положения тела вдоль осей X и Y при 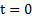 .
.
При движении тела с постоянным ускорением  уравнения движения тела вдоль осей X и Y будут иметь вид
уравнения движения тела вдоль осей X и Y будут иметь вид
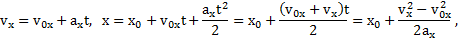
 .
.
Пример 1. Тело движется по закону  . Найти зависимость его скорости и ускорения от времени t.
. Найти зависимость его скорости и ускорения от времени t.
Дано:  . Найти:
. Найти: 
Решение: Согласно условию  . Откуда
. Откуда  и
и 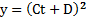 . Компоненты скорости и скорость тела
. Компоненты скорости и скорость тела
 ,
,  ,
,
 .
.
Компоненты ускорения и ускорение тела
 ,
, 
 .
.
Ответ:  ,
,  .
.
Пример 2. Тело движется по закону  . Найти уравнение траектории движения тела и направление движения тела вдоль нее. Чему равны положение тела, его скорость и ускорение в момент времени
. Найти уравнение траектории движения тела и направление движения тела вдоль нее. Чему равны положение тела, его скорость и ускорение в момент времени  ?
?
Дано:  . Найти:
. Найти: 
Решение: Исключая синус и косинус из уравнений движения с помощью тождества  , получаем уравнение траектории тела
, получаем уравнение траектории тела  . Это уравнение эллипса с полуосями A и B. Задавая значения аргумента функций
. Это уравнение эллипса с полуосями A и B. Задавая значения аргумента функций  , получим последовательность точек
, получим последовательность точек  , которая говорит о том, что тело движется из точки
, которая говорит о том, что тело движется из точки 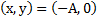 по эллипсу по часовой стрелке (рис.3).
по эллипсу по часовой стрелке (рис.3).
(рис.3)
Положение тела на эллипсе задается координатами x и y, которые с учетом, что при  :
: 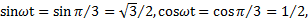 равны
равны  . Расстояние от центра эллипса до тела в момент времени
. Расстояние от центра эллипса до тела в момент времени  равно
равно
 .
.
Компоненты скорости тела  ,
,  . Величина скорости
. Величина скорости
 .
.
Компоненты ускорения 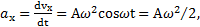
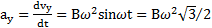 . Величина ускорения
. Величина ускорения
 .
.
Ответ:  , тело движется по эллипсу по часовой стрелке,
, тело движется по эллипсу по часовой стрелке,  ,
,  ,
, 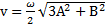 ,
, 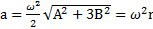 .
.
Пример 3. Тело бросили с высоты  с начальной скоростью
с начальной скоростью 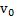 под углом α к горизонту. Найти максимальную высоту его подъема, время и дальность полета.
под углом α к горизонту. Найти максимальную высоту его подъема, время и дальность полета.
Дано:  . Найти:
. Найти: 
Решение: Выберем начало О системы координат XOY на поверхности земли под точкой броска, ось X направим параллельно поверхности земли, а ось Y перпендикулярно к ней (рис.1). В выбранной системе отсчета уравнения движения тела будут иметь вид 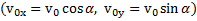

В точке максимального подъема  , поэтому максимальная высота подъема тела
, поэтому максимальная высота подъема тела

Время  полета тела до его падения на землю находим из условия
полета тела до его падения на землю находим из условия  , которое приводит к квадратному уравнению
, которое приводит к квадратному уравнению  . Отсюда находим (t>0)
. Отсюда находим (t>0)
 . Дальность полета тела
. Дальность полета тела  .
.
Ответ: 
Пример 4. Решить предыдущую задачу в предположении, что тело брошено с поверхности земли.
Дано:  . Найти:
. Найти: 
Решение: Повторяя решение примера 1 в предположении  , получим
, получим
 .
.
Ответ:  ,
, 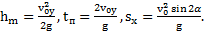
Пример 5. Тело брошено с поверхности земли под углом α к горизонту. При этом оказалось, что дальность его полета в 4 раза больше максимальной высоты подъема тела. Найти угол броска тела.
Дано:  Найти:
Найти: 
Решение: Используя решение примера 4, получим

Отсюда 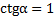 или
или 
Ответ: 
Пример 6. Тело брошено с поверхности земли вертикально вверх и побывало на некоторой высоте в моменты времени 1 с и 2 с. Найти эту высоту и начальную скорость броска камня. Через какое время тело упадет на землю?
Дано:  Найти:
Найти: 
Решение: Выберем начало О системы координат на поверхности земли, а ось Y направим вверх. В выбранной системе отсчета уравнение движения тела имеет вид  . Полагая
. Полагая  , приходим к квадратному уравнению
, приходим к квадратному уравнению  . Решения этого уравнения
. Решения этого уравнения  и
и  соответствуют моментам времени, в которые тело побывало на высоте
соответствуют моментам времени, в которые тело побывало на высоте  . Они должны удовлетворять теореме Виета для квадратного уравнения:
. Они должны удовлетворять теореме Виета для квадратного уравнения: 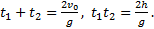 Откуда
Откуда

Время  полета тела до его падения на землю находим из условия
полета тела до его падения на землю находим из условия

Откуда 
Ответ: 
Пример 7. Ракета, запущенная с поверхности земли с начальной скоростью 20  , под углом
, под углом  к горизонту побывала на некоторой высоте с интервалом времени 2 с. Найти эту высоту.
к горизонту побывала на некоторой высоте с интервалом времени 2 с. Найти эту высоту.
Дано:  . Найти:
. Найти: 
Решение: Выберем начало О системы координат XOY на поверхности земли в точке запуска ракеты, ось X направим параллельно поверхности земли, а ось Y перпендикулярно к ней (рис.1). В выбранной системе отсчета уравнение движения тела будут иметь вид  .
.
Полагая  , приходим к квадратному уравнению
, приходим к квадратному уравнению  решение которого имеет вид
решение которого имеет вид  . Отсюда получаем
. Отсюда получаем
 .
.
Откуда высота  ракеты над землей в моменты времени
ракеты над землей в моменты времени  и
и  с учетом, что
с учетом, что  , равна
, равна

Ответ: 
Естественный способ описания движения тела. В этом методе движение тела описывается в системе координат (τ,n), жестко связанной с движущимся телом (рис.4). Такая система отсчета называется естественной. Ось τ направляют в направлении вектора скорости v тела, а ось n перпендикулярно к ней к центру кривизны траектории движения тела. Положение тела на траектории его движения в естественной системе отсчета задают дуговой координатой 
(рис.4)
При движении тела по кривой направления векторов ускорения a и скорости v тела не совпадают. Обозначим  угол между векторами a и v. Проекцию вектора ускорения a на ось τ, равную
угол между векторами a и v. Проекцию вектора ускорения a на ось τ, равную  α, называют касательным (тангенциальным) ускорением, а проекцию a на ось n, равную
α, называют касательным (тангенциальным) ускорением, а проекцию a на ось n, равную  , - нормальным (центростремительным) ускорением тела.
, - нормальным (центростремительным) ускорением тела.
Можно показать, что величина скорости v тела, его касательное  , нормальное
, нормальное  и полное a ускорения тела и угол
и полное a ускорения тела и угол  в еcтественной системе отсчета определяются соотношениями
в еcтественной системе отсчета определяются соотношениями
 ,
,
где  – радиус кривизны траектории в точке нахождения тела.
– радиус кривизны траектории в точке нахождения тела.
При движении по кривой с постоянной скоростью  При движении тела по прямой
При движении тела по прямой 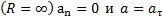 .
.
Изменение скорости  тела и путь
тела и путь  , пройденный им за время t, равны
, пройденный им за время t, равны
 ,
,
где  и
и  – начальные скорость и положение тела относительно выбранного начала отсчета при
– начальные скорость и положение тела относительно выбранного начала отсчета при  .
.
Уравнения движения тела при  имеют вид
имеют вид
 ,
,
где  – проекция вектора a полного ускорения тела на направление скорости v его движения и имеет знак (
– проекция вектора a полного ускорения тела на направление скорости v его движения и имеет знак ( ) или (
) или ( ) при ускоренном и замедленном движении тела.
) при ускоренном и замедленном движении тела.
Пример 1. Тело бросили с поверхности земли с начальной скоростью 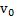 под углом α к горизонту. Найти радиусы кривизны
под углом α к горизонту. Найти радиусы кривизны  и R траектории в точке броска тела и в точке его максимального подъема.
и R траектории в точке броска тела и в точке его максимального подъема.
Дано: 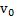 , α, g. Найти:
, α, g. Найти: 
Решение: Выберем начало О системы отсчета XOY в точке броска тела, ось X направим параллельно поверхности земли, а ось Y перпендикулярно к ней. Полное ускорение тела  в данной задаче известно.
в данной задаче известно.
(рис.5)
Нормальное ускорение тела в точке его броска (рис. 5) равно  и радиус кривизны траектории в этой точке
и радиус кривизны траектории в этой точке
 .
.
В верхней точке траектории  и скорость тела
и скорость тела  . Радиус кривизны траектории в верхней точке
. Радиус кривизны траектории в верхней точке

Ответ: 
Пример 2. Тело движется вдоль осей X и Y по закону:  Найти угол
Найти угол  между направлениями векторов скорости
между направлениями векторов скорости  и полного ускорения
и полного ускорения  тела и радиус кривизны
тела и радиус кривизны  траектории в точке, в которой тело окажется в момент времени
траектории в точке, в которой тело окажется в момент времени  .
.
Дано:  Найти:
Найти: 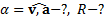
Решени е:  и
и  компоненты скорости тела и его скорость
компоненты скорости тела и его скорость 

 ,
,
 и
и  компоненты ускорения тела и его полное ускорение
компоненты ускорения тела и его полное ускорение 
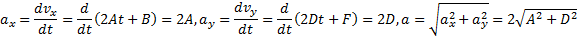
Касательное ускорение  тела
тела
 .
.
Нормальное ускорение  тела
тела
 .
.
Угол  между направлениями векторов
между направлениями векторов  и
и 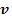 при
при  определяется условием
определяется условием

Радиус  кривизны в точке траектории, в которой тело будет находиться в момент времени
кривизны в точке траектории, в которой тело будет находиться в момент времени  :
:  .
.
Ответ:  ,
,  .
.
Пример 3. Тело бросили под углом α к горизонту с начальной скоростью  . Найти касательное
. Найти касательное  и нормальное
и нормальное  ускорение тела, угол
ускорение тела, угол 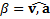 между направлениями векторов
между направлениями векторов  и
и  и радиус
и радиус  кривизны траектории в точке, в которой тело окажется в момент времени t.
кривизны траектории в точке, в которой тело окажется в момент времени t.
Дано:  . Найти:
. Найти: 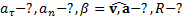
Решение: В данной задаче надо использовать две системы координат: лабораторную XOY и естественную  , выбираемые стандартным образом (рис.6). Полное ускорение тела
, выбираемые стандартным образом (рис.6). Полное ускорение тела  в данной задаче известно.
в данной задаче известно.
Рис.6
Построим алгоритм решения задачи: 


Появление знака  в формулах тригонометрических функций обусловлено тем, что они вычисляются через параметры
в формулах тригонометрических функций обусловлено тем, что они вычисляются через параметры  и
и  , определенными в системе координат XOY, в которой угол
, определенными в системе координат XOY, в которой угол  является отрицательным (отсчитывается от оси Y против часовой стрелки).
является отрицательным (отсчитывается от оси Y против часовой стрелки).
Ответ: 
Вращательное движение
Вращательное движение тела описывается углом поворота тела  , его угловой скоростью ω и угловым ускорением ε, которые являются аналогами величин s, v,
, его угловой скоростью ω и угловым ускорением ε, которые являются аналогами величин s, v,  , используемыми для описания поступательного движения тела. Согласно определению
, используемыми для описания поступательного движения тела. Согласно определению
 .
.
Параметры  являются векторами. Направление векторов
являются векторами. Направление векторов  совпадает с направлением оси вращения тела (рис.7) и связано с ним правилом правого винта: если правый буравчик вращать по направлению вращения тела, то направление его движения укажет направление векторов
совпадает с направлением оси вращения тела (рис.7) и связано с ним правилом правого винта: если правый буравчик вращать по направлению вращения тела, то направление его движения укажет направление векторов  .Вектор ε в случае фиксированной неподвижной оси вращения также направлен вдоль оси вращения. Он параллелен вектору ω при ускоренном вращении тела и антипараллелен ему при его замедленном вращении.
.Вектор ε в случае фиксированной неподвижной оси вращения также направлен вдоль оси вращения. Он параллелен вектору ω при ускоренном вращении тела и антипараллелен ему при его замедленном вращении.
Рис.7
Элементарный поворот d ϕ тела всегда вектор, однако угол поворота тела 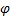 является вектором только при вращении тела вокруг фиксированной оси его вращения.
является вектором только при вращении тела вокруг фиксированной оси его вращения.
Изменение угловой скорости тела Δ ω и угол  его поворота за время вращения тела t равны
его поворота за время вращения тела t равны
 ,
,
где 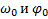 – начальная угловая скорость и начальное угловое положение тела при t=0.
– начальная угловая скорость и начальное угловое положение тела при t=0.
При вращении тела с постоянным угловым ускорением  уравнения вращательного движения имеют вид
уравнения вращательного движения имеют вид
 .
.
где + ε и – ε соответствуют ускоренному и замедленному вращению тела.
Наряду с угловыми величинами 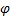 (рад) и ω (рад/с) для описания вращательного движения используются величины N (об) – число оборотов тела и n (об/с) – частота вращения тела, определяемые соотношениями
(рад) и ω (рад/с) для описания вращательного движения используются величины N (об) – число оборотов тела и n (об/с) – частота вращения тела, определяемые соотношениями  и
и  . В терминах этих величин уравнения вращательного движения при
. В терминах этих величин уравнения вращательного движения при  имеют вид
имеют вид

Однако, если ε =0 и  то
то  .Только в этом случае частота вращения тела может рассчитываться по формуле
.Только в этом случае частота вращения тела может рассчитываться по формуле  и можно ввести понятие периода T вращения тела (n=1/T). Это можно отнести к описанию вращения Земли вокруг своей оси.
и можно ввести понятие периода T вращения тела (n=1/T). Это можно отнести к описанию вращения Земли вокруг своей оси.
3. Связь между линейными и угловыми величинами
Угловые величины  для всех точек вращающегося тела относительно любых параллельных осей вращения одинаковы, а линейные величины
для всех точек вращающегося тела относительно любых параллельных осей вращения одинаковы, а линейные величины  различны. Для установления связи между ними используют определение радианной меры угла
различны. Для установления связи между ними используют определение радианной меры угла  , опирающегося на дугу длиной s окружности радиуса R:
, опирающегося на дугу длиной s окружности радиуса R:  и определения линейных величин. В результате получим следующие уравнения связи
и определения линейных величин. В результате получим следующие уравнения связи
 ,
,
где в случае 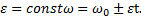 Угол
Угол  между векторами a и v в некоторый момент времени t определяется соотношением
между векторами a и v в некоторый момент времени t определяется соотношением 
рис.8
В теории представляет интерес векторная связь между векторами v и ω: 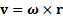 , где r - вектор, проведенный из произвольной точки О на оси вращенияZ в произвольную точку вращающегося тела (рис.8). Направления векторов v и ω cвязаны между собой правилом правого винта. Переходя к скалярной форме, получим
, где r - вектор, проведенный из произвольной точки О на оси вращенияZ в произвольную точку вращающегося тела (рис.8). Направления векторов v и ω cвязаны между собой правилом правого винта. Переходя к скалярной форме, получим  , где
, где  – угол между векторами ω и r,
– угол между векторами ω и r,  расстояние от рассматриваемой точки тела до его оси вращения Z или радиус окружности, по которой эта точка вращается.
расстояние от рассматриваемой точки тела до его оси вращения Z или радиус окружности, по которой эта точка вращается.
Пример 1. Тело, вращающееся по окружности радиуса R с постоянным угловым ускорением, увеличило свою частоту вращения от  до
до  оборотов в секунду, совершив при этом
оборотов в секунду, совершив при этом  оборотов. Найти угловое ускорение вращения тела и время его вращения, угол его поворота, начальную и конечную угловые скорости. Чему равны путь, пройденный телом вдоль окружности, его начальная и конечная скорости, касательное, центростремительное и полное ускорение?
оборотов. Найти угловое ускорение вращения тела и время его вращения, угол его поворота, начальную и конечную угловые скорости. Чему равны путь, пройденный телом вдоль окружности, его начальная и конечная скорости, касательное, центростремительное и полное ускорение?
Дано:  Найти:
Найти: 
Решение: Построим решение задачи в виде последовательного алгоритма. Число оборотов N тела при  дается уравнениями
дается уравнениями
 .
.
Откуда находим угловое ускорение и время вращения тела
 .
.
Угол поворота и угловые скорости тела:  . Линейные величины:
. Линейные величины:  .
.
Ответ:  ,
,  ,
,
 .
.
Относительное движение
Рассмотрим произвольную неподвижную систему отсчета XOY с началом в точке О, и движущуюся систему отсчета  , положение начала координат которой
, положение начала координат которой  относительно точки О задается радиус-вектором
относительно точки О задается радиус-вектором  , а точка
, а точка  движется относительно XOY со скоростью
движется относительно XOY со скоростью  и ускорением
и ускорением  .Обозначим через
.Обозначим через  положение, скорость и ускорение некоторой точки (она может принадлежать и твердому телу) в системе координат XOY, а через
положение, скорость и ускорение некоторой точки (она может принадлежать и твердому телу) в системе координат XOY, а через  те же параметры этой точки в системе координат
те же параметры этой точки в системе координат 
Рис.9
Учитывая, что  (рис.9) и последовательно дифференцируя по времени обе части этого равенства, придем к следующим уравнениям связи
(рис.9) и последовательно дифференцируя по времени обе части этого равенства, придем к следующим уравнениям связи

между скоростями 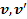 и ускорениями
и ускорениями  рассматриваемойточки в неподвижной и движущейся системах отсчета.
рассматриваемойточки в неподвижной и движущейся системах отсчета.
Движение в неподвижной СО называют также абсолютным, движение подвижной СО относительно неподвижной – переносным, а движение тела в движущейся СО – относительным.
Пример 1. Тело, движущееся со скоростью  , сталкивается абсолютно упруго с движущейся со скоростью
, сталкивается абсолютно упруго с движущейся со скоростью  вертикальной массивной стенкой. Найти скорость тела после соударения со стенкой.
вертикальной массивной стенкой. Найти скорость тела после соударения со стенкой.
Дано:  . Найти:
. Найти: 
Решение: Будем считать стенку, движущуюся со скоростью  , движущейся системой отсчета. Обозначим
, движущейся системой отсчета. Обозначим  скорость тела в этой системе отсчета. Тогда скорость те
скорость тела в этой системе отсчета. Тогда скорость те  ладо его столкновения
ладо его столкновения
 . После столкновения со стенкой тело вследствие абсолютно упругого удара приобретет относительно стенки скорость
. После столкновения со стенкой тело вследствие абсолютно упругого удара приобретет относительно стенки скорость  , и его скорость станет равной
, и его скорость станет равной  . Из этих двух уравнений получим:
. Из этих двух уравнений получим:  .
.
В проекциях на направление движения тела и стенки при их встречном движении получим  . В случае же движения стенки и тела в одном направлении
. В случае же движения стенки и тела в одном направлении  . Отсюда следует: если стенка движется от тела со скоростью
. Отсюда следует: если стенка движется от тела со скоростью 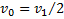 , то тело после столкновения с ней остановится
, то тело после столкновения с ней остановится  .Чтобы тело отскочило от удаляющейся стенки, она должна удаляться от него со скоростью
.Чтобы тело отскочило от удаляющейся стенки, она должна удаляться от него со скоростью  .
.
Ответ:  .
.
Пример 2. Скорость струи пара перед попаданием на лопатки паровой турбины равна 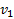 . Какой должна быть скорость
. Какой должна быть скорость  лопаток, чтобы вся кинетическая энергия струи пара могла перейти в энергию вращения турбины?
лопаток, чтобы вся кинетическая энергия струи пара могла перейти в энергию вращения турбины?
Решение: Чтобы вся кинетическая энергия струи пара перешла в энергию вращения турбины, его скорость после отражения от лопаток должна равняться нулю  . Согласно примеру 1 получим
. Согласно примеру 1 получим 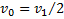 . Это соотношение выполняется в рабочем режиме турбины.
. Это соотношение выполняется в рабочем режиме турбины.
Ответ: 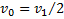 .
.
Пример 3. Два автомобиля движутся по одной дороге. Скорость первого автомобиля  , а второго –
, а второго –  . Найти относительную скорость движения автомобилей при их движении в одном направлении и навстречу друг другу.
. Найти относительную скорость движения автомобилей при их движении в одном направлении и навстречу друг другу.
Дано:  . Найти:
. Найти: 
Решение: Свяжем с первым автомобилем движущуюся СО. Тогда  , а относительная скорость второго автомобиля относительно первого
, а относительная скорость второго автомобиля относительно первого  , его абсолютная скорость относительно земли
, его абсолютная скорость относительно земли  . Откуда относительная скорость автомобилей
. Откуда относительная скорость автомобилей  .
.
При движении автомобилей в одном направлении в проекциях на направление их движения получим  . При встречном движении автомобилей в проекциях на направление движения любого из автомобилей:
. При встречном движении автомобилей в проекциях на направление движения любого из автомобилей:  .
.
Ответ:  при движении автомобилей в одном направлении,
при движении автомобилей в одном направлении,  при встречном движении автомобилей.
при встречном движении автомобилей.
Пример 4. Два тела бросают с поверхности земли вертикально вверх с начальными скоростями  и
и  с задержкой по времени, равной τ. Найти относительную скорость движения тел в произвольный момент времени.
с задержкой по времени, равной τ. Найти относительную скорость движения тел в произвольный момент времени.
Дано:  . Найти:
. Найти: 
Решение: проекции абсолютных скоростей тел на вертикальное направление их движения равны 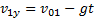 и
и  . Проекция относительной скорости тел на вертикальное направление
. Проекция относительной скорости тел на вертикальное направление  . Относительная скорость тел
. Относительная скорость тел  в любой момент времени одинакова.
в любой момент времени одинакова.
Ответ:  .
.
Пример 5. Два тела движутся в одной плоскости, их скорости изменяются по закону  ,
,  . Найти скорость движения их ЦМ, импульс системы и скорости тел относительно их ЦМ. Отличаются ли относительные скорости тел в неподвижной СО и в системе их ЦМ?
. Найти скорость движения их ЦМ, импульс системы и скорости тел относительно их ЦМ. Отличаются ли относительные скорости тел в неподвижной СО и в системе их ЦМ?
Дано:  ,
,  . Найти:
. Найти: 
Решение: Система понятий, используемых в данной задаче, введена в разделах 7 и 12 (Центр масс и второй закон Ньютона для системы тел). Задачу будем решать в векторной форме. Скорость ЦМ системы двух точек


Импульс системы совпадает с импульсом ее ЦМ:  .
.
Если скорость тела относительно ЦМ  , а скорость ЦМ относительно земли
, а скорость ЦМ относительно земли 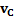 , то скорость тела относительно земли
, то скорость тела относительно земли  , откуда
, откуда  . В частности,
. В частности,
 ,
, 
 ,
, 
Скорости тел относительно друг друга в неподвижной СО и системе ЦМ
 ,
,
то есть относительные скорости тел в обеих системах отсчета одинаковы.
Ответ:  ,
,  ,
,  ,
,
 ,
,  .
.