Согласно уравнениям вращательного движения 
, 
момент импульса тела или системы тел сохраняется, если момент внешних сил, действующих на систему 
(замкнутая система тел). Тогда 
и 
. Наиболее часто встречается случай, когда в направлении некоторой оси, например Z, 
(система замкнута в направлении оси Z). В этом случае 
и 
.
В быстрых процессах (удар, столкновения тел) длительность процесса 
и согласно уравнению вращательного движения в интегральной форме 
или .
Пример 1. К концу нити, накрученной на цилиндрический блок радиуса R и массой M, привязано тело массой m. Тело поднимают на высоту 
и отпускают. После упругого рывка нити тело отскакивает на высоту 
(рис.65). Какое количество теплоты выделилось при рывке? Чему будет равна угловая скорость вращения блока сразу же после рывка?
Рис.65
Дано: 
. Найти: 
Решение: Скорости тела до и после рывка нити равны 
и 
. Тепло, выделившееся при рывке, согласно закону сохранения энергии: 
.
Рывок нити – быстрый процесс, и при рывке имеет место закон сохранения момента импульса системы блок-тело: 
. Откуда угловая скорость вращения блока сразу же после рывка 
.
Ответ: 
.
Пример 2. Человек массой m стоит на краю круглой платформы массой M и радиусом R, вращающейся с угловой скоростью 
. Какой станет угловая скорость вращения платформы, если человек перейдет на расстояние R/2 от ее центра?
Дано: 
Найти: 
Решение: В системе действуют только силы, параллельные оси вращения Z, перпендикулярной плоскости платформы. Поэтому имеет место закон сохранения момента импульса системы относительно оси Z. Начальный момент импульса системы 
. После перехода человека на середину платформы 
. Из условия 
получим 
, откуда 
.
Ответ: .
Пример 3. Человек массой m, находящийся на краю платформы массой M и радиусом R, начинает двигаться вдоль края платформы с линейной скоростью 
. Найти угловую скорость вращения платформы, считая человека материальной точкой. Может ли она быть больше угловой скорости движения человека?
Рис.66
Дано: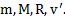 
Найти: 
Решение: В системе действуют силы, параллельные оси вращения Z, перпендикулярной плоскости платформы(рис.66). Поэтому имеет место закон сохранения момента импульса системы относительно оси Z.
Задачу будем решать в векторной форме. В задаче две системы отсчета с общей осью вращения Z: неподвижная, связанная с землей, и вращающаяся, связанная с платформой. При движении человека с угловой скоростью 
относительно оси вращения платформы она придет во вращательное движение относительно земли с угловой скоростью 
, и угловая скорость человека относительно земли будет равна 
.
Момент импульса системы платформа-человек согласно закону его сохранения в СО, связанной с землей (параметры тел в законе сохранения в начальной его формулировке должны быть заданы в одной и той же СО), будет равен
.
Откуда угловая скорость вращения платформы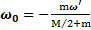 
. Знак минус говорит о том, что платформа и человек вращаются относительно оси Z в противоположных направлениях. В скалярной форме 
. Продифференцировав или проинтегрировав обе части этого равенства по времени, получим, что связь между ускорениями 
и 
иуглами поворота 
и 
человека и платформы вокруг оси Z будет иметь аналогичный вид. Отношение угловых скоростей платформы и человека 
. Это означает, что всегда 
.
Ответ: , всегда .