Из уравнения связи 
, обозначив 
, придем к уравнению 
, называемому дифференциальным уравнением гармонических колебаний или уравнением гармонического осциллятора без затухания. Его решением является функция 
. Величина 
называется собственной частотой колебаний системы без затухания.
Собственная частота и период 
колебаний математического маятника (материальной точки подвешенной на нерастяжимой нити длиной l): 
, 
. Для пружинного маятника – 
, 
, где m – масса тела, подвешенного к пружине с жесткостью k.
Рис.73
Для физического маятника (тела с распределенной массой m), центр масс которого находится на расстоянии 
от оси колебаний О (рис.73) и он по теореме Штейнера имеет момент инерции 
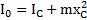относительно этой оси: 
, 
. Период колебаний физического маятника можно представить в виде 
, где величина 
называется приведенной длиной физического маятника, который колеблется с тем же периодом, что и математический маятник на нити длиной 
.
Если 
определить экспериментально, то можно найти момент инерции тела со сложной конфигурацией, рассчитать который теоретически довольно сложно. Для этого надо найти новую ось качания маятника 
, относительно которой он колеблется с тем же периодом 
, что и относительно начальной оси колебаний O. Расстояние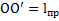 
и будет приведенной длиной физического маятника (рис.73). Приведенную длину маятника можно найти также по определенному экспериментально периоду собственных колебаний маятника , тогда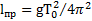 
.
Положение ЦМ тела определяется путем нахождения точки равновесия тела либо путем подвешивания тела в двух точках. Если провести из точек подвеса тела две прямые в направлении его силы тяжести, то пересечение этих прямых даст положение ЦМ тела.
Пример 1. Найти период колебаний стержня длиной l и массой m с насаженным на него диском радиусом R и массой M, находящимся на расстоянии 
длины стержня от его конца, если стержень подвешен на расстоянии 
его длины от его второго конца. Ось колебаний перпендикулярна плоскости диска.
Дано: l, m, R, M. Найти: 
Решение: Решение задачи построим в виде последовательного алгоритма. Центры масс стержня и диска находятся на расстоянии 
и 
от точки подвеса О. Положение общего центра масс системы относительно точки О 
. Собственные моменты инерции тел 
и 
. Моменты инерции тел относительно точки О по теореме Штейнера 
и 
. Полный момент инерции системы относительно точки О 
. Период колебаний физического маятника 
.
Ответ: 
.
Пример 2. На каком расстоянии от ЦМ надо подвесить физический маятник, собственный момент инерции которого рассчитывается по формуле 
, чтобы его период колебаний был минимальным? Рассмотреть случаи стержня длиной l, равностороннего треугольника с длиной стороны b и круглых тел радиуса R – диска (сплошного цилиндра), кольца (полого цилиндра), шара и сферы.
Дано: 
длина стороны треугольника, для круглых тел 
, 
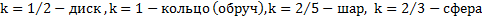. Найти: 
Решение: Период колебаний физического маятника
Период колебаний маятника минимален 
, если подкоренная функция 
или 
. Откуда 
. Подставляя 
получим 
. Минимальный период колебаний маятника 
.
Ответ: 
, 
.
Пример 3. Найти период колебаний круглых тел (обруча или полого цилиндра, диска или сплошного цилиндра, шара) относительно оси колебаний проходящей вдоль их образующей (вдоль края кольца и диска перпендикулярно их плоскости). Во сколько раз отличается этот период от минимального периода колебаний маятника?
Дано: 
, 
. Найти: 
Решение: Момент инерции круглых тел относительно оси, проходящей вдоль их образующей, равен 
. Период колебания маятника относительно этой оси 
. С учетом примера 2 отношение периодов колебаний 
Ответ: 
,
Пример 4. В опыте найдено положение двух осей О и физического маятника массой m, находящихся по разные стороны от его ЦМ, на расстояниях и 
от него, относительно которых он колеблется с одинаковым периодом. Найдите приведенную длину, период собственных колебаний и собственный момент инерции маятника, и его моменты инерции относительно осей О и .
Дано: 
. Найти: 
Решение: Согласно формуле для периода колебаний физического маятника и определению его приведенной длины 
. Отсюда следует, что расстояния и от ЦМ маятника до осей колебания и качания маятника O и являются корнями квадратного уравнения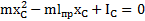 
. Согласно теореме Виета корни это уравнения удовлетворяют соотношениям 
и 
. Откуда 
. Моменты инерции маятника относительно осей O и равны 
и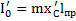 
.
Ответ: 
.