После получения начального решения (опорного плана) для получения оптимального плана перемещения груза используется итерационный алгоритм, основу которого составляют понятия потенциала и цикла.
Для перехода от одного базиса к другому при решении транспортной задачи используются так называемые циклы.
Циклом пересчёта в таблице перевозок называется последовательность неизвестных, удовлетворяющая следующим условиям:
1. Одно из неизвестных последовательности свободное, а все остальные – базисные.
2. Каждые два соседних в последовательности неизвестных лежат либо в одном столбце, либо в одной строке.
3. Три последовательных неизвестных не могут находиться в одном столбце или в одной строке.
4. Если, начиная с какого-либо неизвестного, мы будем последовательно переходить от одного к следующему за ним неизвестному, то через несколько шагов мы вернёмся к исходному неизвестному.
Второе условие означает, что у двух соседних неизвестных в цикле либо первые, либо вторые индексы одинаковы.
Если каждые два соседних неизвестных цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в свободной клетке, а остальные – в базисных клетках.
Можно доказать, что для любой свободной клетки таблицы перевозок существует один и только один цикл, содержащий свободное неизвестное из этой клетки, и что число вершин в цикле всегда чётно.
Пусть теперь мы имеем некоторую свободную клетку с соответствующим ей циклом. Если мы изменим значение свободного неизвестного, увеличив его на некоторое число х, то, переходя последовательно от одной вершины цикла к другой, мы должны будем в силу неизменности сумм по строкам и по столбцам поочередно уменьшать и увеличивать значения неизвестных в цикле на то же число х.
Очевидно, если снабдить вершины цикла поочередно знаками
«+» и «–», приписав вершине в свободной клетке знак «+», то можно сказать, что в вершинах со знаком «+» число х прибавляется к прежнему значению неизвестного, находящегося в этой вершине, а в вершинах со знаком «–» это число х вычитается из прежнего значения неизвестного, находящегося в этой вершине.
Если в качестве х выбрать наименьшее из чисел, стоящих в вершинах, снабженных знаком «–», то по крайней мере одно из прежних базисных неизвестных примет значение нуль, и мы можем перевести его в число свободных неизвестных, сделав вместо него базисным то неизвестное, которое было свободным.
Выбор в качестве х минимальное среди чисел, стоящих в отрицательных вершинах цикла, обеспечивает допустимость нового базиса.
Если минимальное значение среди базисных неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной отрицательной вершине, то свободной оставляют только одну из них, а в других клетках с тем же минимальным значением пишут нули. В этом случае новое базисное решение будет вырожденным. Может случиться, что и само минимальное значение среди чисел в отрицательных клетках равно нулю. Тогда преобразование таблицы перевозок сведётся к перестановке этого нуля в свободную клетку. Значения всех неизвестных при этом остаются неизменными, но решения считаются различными, так как различны базисы. Оба решения вырождены.
Описанное выше преобразование таблицы перевозок, в результате которого преобразуется базис, называется пересчётом по циклу.
Заметим, что неизвестные, не входящие в цикл, этим преобразованием не затрагиваются, их значения остаются неизменными, и каждое из них остаётся либо в группе базисных, либо в группе свободных неизвестных, как и до пересчёта.
Выясним теперь, как пересчет по циклу влияет на общий объём затрат на перевозки и при каком условии эти затраты становятся меньше.
Пусть хpq – некоторое свободное неизвестное, для которого мы построили цикл и осуществили пересчёт по циклу с некоторым числом х. Если вершине цикла, находящейся в i -й строке и j -м столбце таблицы перевозок, приписан знак «+», то значение неизвестного хij, находящегося в этой вершине, увеличивается на х, что в свою очередь вызывает увеличение затрат на сijх, где сij – тариф, соответствующий этой клетке; если же указанной вершине приписан знак «–», то значение неизвестного хij уменьшается на х, что вызывает уменьшение затрат на сijх.
Сложим тарифы, соответствующие положительным вершинам цикла, и вычтем из этой суммы сумму тарифов, соответствующих отрицательным вершинам цикла; полученную разность Spq назовём алгебраической суммой тарифов для данного свободного неизвестного хpq. Подсчёт алгебраической суммы тарифов можно истолковать и так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком («относительных тарифов»).
Теперь, очевидно, мы можем заключить, что в целом при пересчёте по циклу, соответствующему свободному неизвестному хpq общий объём затрат на перевозки изменится на произведение алгебраической суммы тарифов на х, т. е. на величину Spqх. Следовательно, если алгебраическая сумма тарифов для некоторого свободного неизвестного хpq отрицательна (Spq < 0), то пересчёт по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна (Spq >0), то пересчёт по соответствующему циклу приведёт к увеличению общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю (Spq = 0), то пересчёт по соответствующему циклу не изменит общую сумму затрат (два различных базисных плана требуют одинаковых затрат на их реализацию).
Рассмотрим цикл на примере в таблице перевозок, составленной по диагональному методу.
Рисунок 6.8 – Пояснение №1 методу потенциалов
Свободн8ой (небазисной переменной) х31 соответствует цикл х31, х33, х13, х11, х31.
В указанном выше цикле для свободного неизвестного х31 получим:
старые значения: х31 = 0, х33 = 25, х13 = 5, х11 = 20;
новые значения: х´31 = х, х'33 = 25 – х, x´13 = 5 + х, х'11 = 20 – х.
Так, в рассмотренном выше цикле имеем отрицательные вершины х33 и х11; следовательно, выбрав х = min{20;25} = 20, мы получаем: старые значения х31 = 0, х33 = 25, х13 = 5, х11 = 20; новые значения: х´31 = 20, х'33 = 5, x´13 = 25, х'11 = 0.
Переменная х31 стала базисной, а переменная х11 небазисной, т.е. вместо прежнего базисного решения получаем новое базисное решение:
Рисунок 6.9 – Пояснение №2 методу потенциалов
Для циклах31, х33, х13, х11, х31 в рассмотренной задаче алгебраическая сумма тарифов:
S21 = c31 – c33 + c13 – c11 = 5 –10 + 30 –10 = 15 > 0.
Значит, пересчёт по этому циклу не снижает расходы. И действительно, осуществив такой пересчёт, мы получаем план, по которому объём перевозок составит:
S2 = 20·5 + 5·10 + 15·20 + 25·30 +5·20 = 1300.
Тогда как по исходному плану он составил S1 = 1000. Имеем увеличение объёма перевозок на 300 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в данном случае равна 15, а пересчёт по циклу осуществляется с помощью числа х = 20 (изменение затрат равно -15·20 = 300).
Теперь рассмотрим цикл на примере в таблице перевозок, составленной по методу наименьшей стоимости.
Рисунок 6.10 – Пояснение №3 методу потенциалов
Неизвестному х11 соответствует цикл х11, х13, х33, х31, х11.
В указанном выше цикле для свободного неизвестного х11 получим:
старые значения: х11 = 0, х13 = 30, х33 = 5, х13 = 20;
новые значения: х´11 = х, х'13 = 30 – х, x´33 = 5 + х, х'31 = 20 – х.
Так, в рассмотренном выше цикле имеем отрицательные вершины х13 и х31; следовательно, выбрав х = min{20;30} = 20, мы получаем:
старые значения х11 = 0, х13 = 30, х33 = 5, х13 = 20;
новые значения: х´11 = 20, х'13 = 10, x´33 = 25, х'31 = 0,
т. е. вместо прежнего базисного решения получаем новое базисное решение:
Рисунок 6.11 – Пояснение №4 методу потенциалов
Для цикла х11, х13, х33, х31, х11 в рассмотренной задаче алгебраическая сумма тарифов:
S21 = c11 – c13 + c33 – c31 = 10 –30 + 10 –5 = -15 < 0.
Значит, пересчёт по этому циклу снижает расходы. И действительно, осуществив такой пересчёт, мы получаем план, по которому объём перевозок в тонно-километрах составит:
S2 = 20·10 + 10·30 + 5·10 +20·10 + 25·10 = 1000.
Тогда как по исходному плану он составил S1 = 1300:
S1 = 20·5 + 5·10 + 15·20 + 25·30 +5·20 = 1300.
Имеем снижение объёма перевозок на 300 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в данном случае равна 15, а пересчёт по циклу осуществляется с помощью числа х = 20 (изменение затрат равно -15·20 = -300).
Вычисление алгебраической суммы тарифов для каждого из свободных неизвестных можно производить без построения соответствующего цикла, пользуясь так называемыми потенциалами. Припишем каждой базе Ai некоторое число ui и каждому потребителю Вj – некоторое число νj:
Ai → ui (i = 1,2, …, m) Bj → vj (j =1,2,..., n),
так что
| ui + vj=cij, | (6.4) |
где cij – тарифы, соответствующие клеткам, заполненным базисными неизвестными. Эти числа ui и νj называются потенциалами соответствующих баз и потребителей.
Зная потенциалы, легко вычислить алгебраическую сумму тарифов. Действительно, если в алгебраической сумме тарифов по циклу, соответствующему свободному неизвестному xpq, заменить тарифы базисных клеток их выражениями через потенциалы по формулам (6.4), то в силу чередования знаков при вершинах цикла все потенциалы, кроме uр и νq, сократятся, и мы получим:
Spq = cpq – (up + νq).
Для базисных клеток сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке; если же
клетка для неизвестного xpq свободная, то сумму потенциалов
| up + νq = c´pq | (6.5) |
называют косвенным тарифом этой клетки. Следовательно, алгебраическая
сумма тарифов для свободной клетки xpq равна разности её настоящего («истинного») и косвенного тарифов:
| Spq = cpq – c´pq. | (6.6) |
Из (6.6) следует, что если косвенный тариф для данной свободной клетки больше её истинного тарифа, то алгебраическая сумма тарифов по циклу, соответствующему этой клетке, будет отрицательна; если же косвенный тариф меньше истинного, то алгебраическая сумма тарифов положительна, и, наконец, если косвенный тариф равен истинному, то алгебраическая сумма тарифов равна нулю.
Потенциалы можно найти из системы равенств (6.4), рассматривая их как систему m + n – 1 уравнений с m + n неизвестными. Так как неизвестных здесь на единицу больше, чем уравнений, то по крайней мере один из потенциалов мы можем выбрать произвольно, положив, например, u1 = 0; тогда остальные потенциалы легко определяются из уравнения (6.4).
Применим метод потенциалов для двух рассмотренных выше опорных
планов. Для плана, полученного по методу северо-западного угла, имеем
Рисунок 6.12 – Пояснение №5 методу потенциалов

Система содержит пять уравнений с шестью неизвестными. Выбирая произвольно значение u1, находим последовательно из первых трёх уравнений значения ν1 = 10 – u1, ν2 = 20 – u1, ν3 = 30 – u1, затем из четвёртого уравнения – u2 = 30 – ν3, из пятого уравнения – u3 = 10 – ν3.
Положив, например, u1 = 0, получаем значения потенциалов:
u1 = 0; ν1 = 10; ν2 = 20; ν3 = 30; u2 = -10; u3 = -20.
Найдём теперь косвенные тарифы для свободных клеток и сравним их с истинными тарифами:




Так как все косвенные тарифы не больше истинных тарифов, то мы получили оптимальный план. В данном случае начальный план, полученный по методу северо-западного угла, представляет собой и оптимальный план.
Произведём аналогичные вычисления для плана, полученного по методу наименьшей стоимости.
Рисунок 6.13 – Пояснение №6 методу потенциалов

Положив аналогично u1 = 0, получаем значения потенциалов:
u1 = 0; ν3 = 30; u2 = -10; ν2 = 20 u3 = -20; ν1 = 25.
Найдём косвенные тарифы для свободных клеток и сравним их с истинными тарифами:
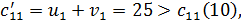



Для клетки с неизвестными х11 косвенный тариф больше истинного. Следовательно, для них мы будем иметь отрицательные алгебраические суммы тарифов:
S11 = c11 - c '11 =10 - 25 = -15.
Это означает, что стоимость перевозки груза можно уменьшить (создать новый план перевозки). Свободная переменная х11 должна быть переведена в базис. Для определения исключаемой из базиса переменной необходимо по строить цикл с началом в клетке с х11.
Цикл (1,1), (1,3), (3,3), (3,1), (1,1) – вершины цикла помечены значками плюс (+) и минус (-).
Рисунок 6.14 – Пояснение №7 методу потенциалов
В указанном выше цикле для свободного неизвестного х11 получим:
старые значения: х11 = 0, х13 = 30, х33 = 5, х13 = 20;
новые значения: х´11 = х, х'13 = 30 – х, x´33 = 5 + х, х'31 = 20 – х.
Так, в рассмотренном выше цикле имеем отрицательные вершины х13 и х31; следовательно, выбрав х = min{20;30} = 20, мы получаем:
старые значения х11 = 0, х13 = 30, х33 = 5, х13 = 20;
новые значения: х´11 = 20, х'13 = 10, x´33 = 25, х'31 = 0,
т. е. вместо прежнего базисного решения получаем новое базисное решение:
Рисунок 6.15 – Пояснение №8 методу потенциалов
S2 = 20·10 + 10·30 + 5·10 +10·20 + 25·10 = 1000.
Полученное решение было улучшено на 1300 – 1000 = 300 тонно-километров. Продолжим вычисления подобно вышеописанному, определим новые потенциалы.

Положив, например, u1 = 0, получаем значения потенциалов:
u1 = 0; ν1 = 10; ν2 = 20; ν3 = 30; u2 = -10; u3 = -20.
Найдём теперь косвенные тарифы для свободных клеток и сравним их с истинными тарифами:
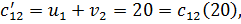



Так как все косвенные тарифы не больше истинных тарифов, то мы получили оптимальный план.
S2 = 20·10 + 10·30 + 5·10 + 10·20 + 25·10 = 1000.