При определении коэффициента местного сопротивления (в данном случае внезапного расширения) необходимо иметь в виду, что за местным сопротивлением, где поток претерпевает значительную деформацию лежит достаточно протяженный «участок стабилизации», на котором существуют крупные вихри с возвратными течениями. Поэтому экспериментальный коэффициент местного сопротивления должен учитывать полные потери на участке стабилизации, а значит должен явно зависеть от числа Рейнольдса. Совпадение с теоретической формулой Борда можно ожидать только при весьма больших числах Рейнольдса.
Расчетными соотношениями для определения коэффициента местного сопротивления по экспериментальным данным являются следующие:
из уравнения Бернулли для двух сечений следует
| (18) |
где hвн.р - искомые потери на внезапном расширении.
Здесь сечение 2 выбирается на расстоянии достаточном для расширения потока на все сечение ω2. Отнеся потери к скоростному напору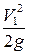 
получим
| (19) |
Разности пьезометрических напоров 
определяется по пьезометрам, а скорость 
по расходу, измеренному ротаметрами. Тогда формула (19) позволяет вычислить экспериментальное значение 
.Результаты вычислений заносятся в таблицу 6. Отклонение расчетного значения коэффициента от опытного (погрешность) определяется по формулам (14) и (15).
Измерив пьезометрами давления во всех точках их подключения, можно построить пьезометрическую линию вдоль трубы, а также напорную линию (см. лабораторную работу №1). Студентам рекомендуется объяснить физическую сущность полученных графиков, а также обозначить на них потери напора в местном сопротивлении.
По результатам измерения расходов для каждого опыта определяются значения чисел Рейнольдса (за местным сопротивлением) по формуле (13) и строится график зависимости коэффициент местного сопротивления от числа Рейнольдса. При этом по оси абсцисс откладывают числа Рейнольдса, по оси ординат – значения коэффициентов. . По графику следует проанализировать изменение коэффициента местного сопротивления в зависимости от числа Рейнольдса и сделать выводы.
Контрольные вопросы к лабораторной работе №4
1. Что такое местное сопротивление?
2. Привести примеры местных сопротивлений?
3. Почему в местах возникновения местных сопротивлений происходит увеличение потерь напора?
4. По какой формуле определяются местные потери напора в общем случае?
5. От чего зависит коэффициент местного сопротивления?
6. Как рассчитать потерю напора при внезапном расширении?
7. Как можно определить потерю напора при внезапном расширении опытным путем?
Таблица 5 – Протокол проведения эксперимента
| № | Показания ротаметров | Показания пьезометров, м | |||||||||||||
| РМ-0,16 | РМ-0,4 | РМ-1,6 | h1 | h2 | ….. | ….. | ….. | ….. | ….. | ….. | hn | ||||
| отметки шкалы | л/ч | отметки шкалы | л/ч | отметки шкалы | л/ч | ||||||||||
| …… | |||||||||||||||
Таблица 6 – Обработка экспериментальных данных
| № | Расход воды, Q, м3/с | Показания контрольных пьезометров | Разность пьезометрических напоров h2- h1, м | Скорость
 , м/с
| Число Рейнольдса,
| Коэффициент местного сопротивления,
| Погрешность | ||||
| h1, м | h2, м | опытный (ф.19) | расчётный (ф. 17) | абсолютная
Δ
| относительная δ, % | ||||||
| …… | |||||||||||
ЛАБОРАТОРНАЯ РАБОТА №5
ИСПЫТАНИЯ МЕРНОЙ ДИАФРАГМЫ
Цель работы:
Опытным путем определить величину коэффициента расхода нестандартной диафрагмы и его зависимость от числа Рейнольдса.
Общие сведения
Диафрагма является частным типом сужающих устройств, применяемых для измерения расхода. Основным параметром, характеризующим диафрагму как расходомера, является ее коэффициент расхода 
, входящей в основную расчетную формулу
| (20) |
где ω0 - площадь отверстия диафрагмы,
p1 и p2 - давления в сечениях, расположенных непосредственно перед диафрагмой и за ней (рисунок 7).
Коэффициент расхода зависит от ряда геометрических параметров (например, от степени сжатия потока диафрагмой, от формы кромки ее отверстия, от расположения точек определения давлений и др.), а также от числа Рейнольдса. Диафрагмы являются широко применяемыми в технике расходомерами и потому многократно испытаны, их параметры и конструкции стандартизованы и занесены в ГОСТы. В настоящей работе ставится задача познакомить студентов с постановкой лабораторного эксперимента по определению величины коэффициента расхода конкретной нестандартной диафрагмы и его зависимости от числа Рейнольдса.