Уравнения непрерывности, Лапласа и Пуассона
Уравнение непрерывности (закон сохранения заряда) выводится из первого уравнения Максвелла в дифференциальной форме:
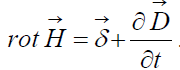
Применим оператор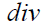 
ко всем членам этого уравнения. Получим
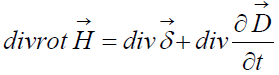
Так как
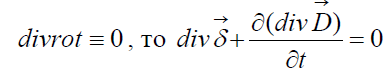
С учётом третьего уравнения Максвелла (1.11) можно записать
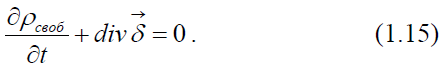
Полученное выражение называется законом сохранения заряда или уравнением непрерывности линий полного тока. Для получения закона сохранения заряда в интегральной форме проинтегрируем уравнение (1.15) по объёму V. Получим
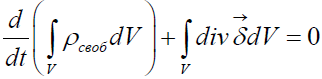
Воспользовавшись теоремой Остроградского-Гаусса (1.7), запишем интегральную форму закона сохранения заряда:
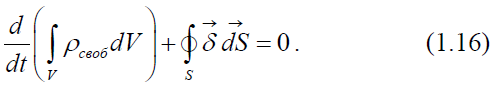
Физический смысл этого уравнения: ток проводимости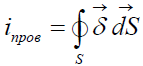 
обусловлен движением свободных зарядов 
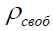или заряд не может перемещаться из одной точки в другую, не создав между ними тока.
Уравнения Пуассона и Лапласа для скалярного потенциала ϕ являются основными дифференциальными уравнениями электростатики. Они следуют из третьего уравнения Максвелла: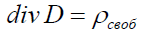 
. Так как
а 
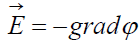то
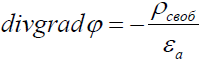
Оператор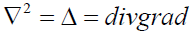 
называют оператором Лапласа или лапласианом. Поэтому можно записать, что
Это уравнение называют уравнением Пуассона.
Если свободных зарядов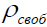 
нет, то уравнение Пуассона переходит в уравнение Лапласа:
В декартовой системе координат уравнения Пуассона и Лапласа имеют вид:
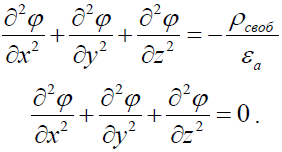
Уравнение энергетического баланса электромагнитного поля (теорема Умова-Пойнтинга)
Кроме уравнений Максвелла и закона сохранения заряда, большое значение в теории электромагнитного поля имеет теорема Умова-Пойнтинга, которая описывает энергетические соотношения распределения полей в заданном объёме. Её не сложно получить из уравнений Максвелла.
Для вывода теоремы Умова-Пойнтинга воспользуемся первым и вторым уравнениями Максвелла в дифференциальной форме, записанными с учётом материальных уравнений (1.1), (1.2), (1.6).
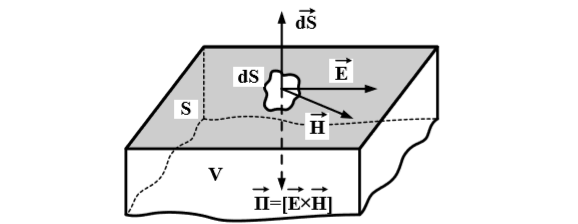
В окончательном виде теорема Умова-Пойнтинга в дифференциальной форме записи имеет вид
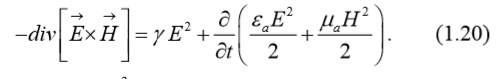
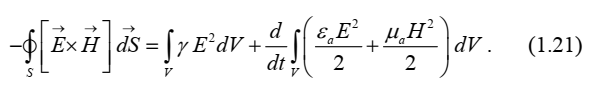
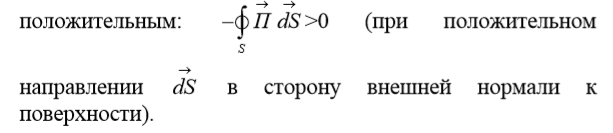
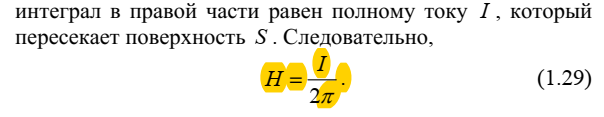
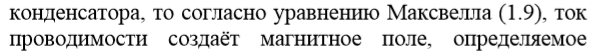
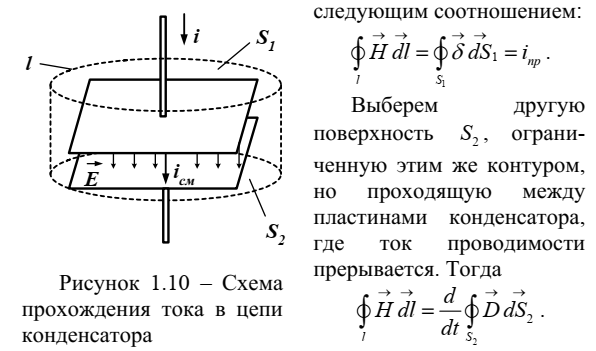
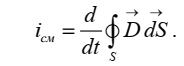
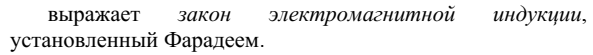
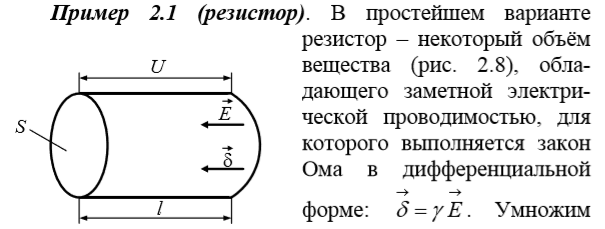
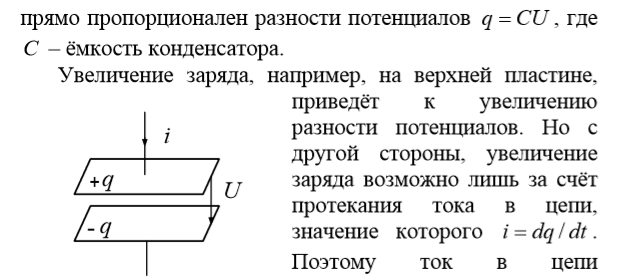
Пример 1.5 (уравнение непрерывности)
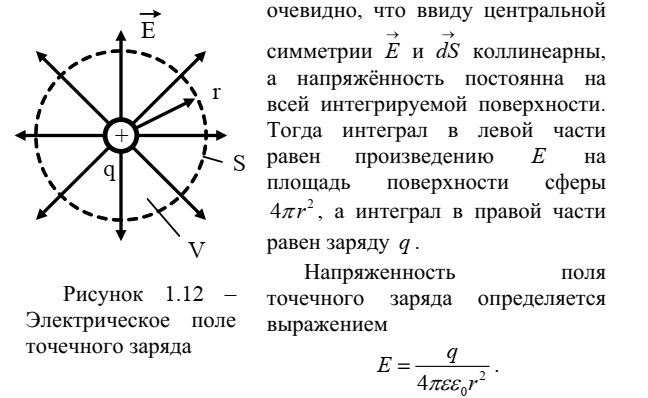
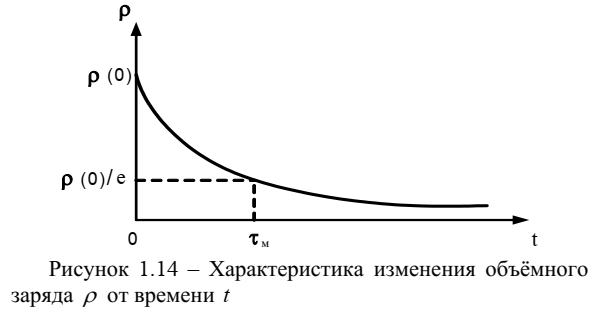
Если в однородной среде, характеризующейся удельной электропроводностью γ, каким-либо образом создать объемный заряд ρ, то очевидно, что за счет токов проводимости этот
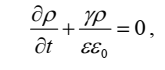
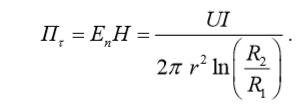
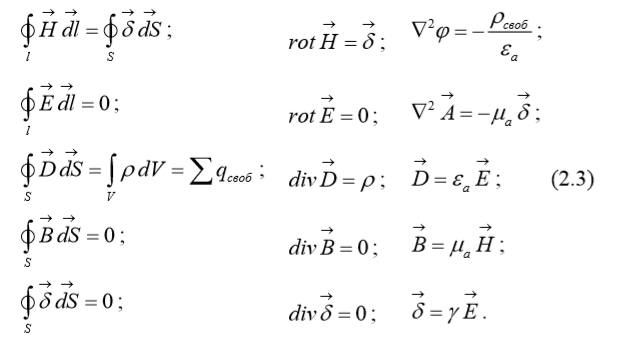
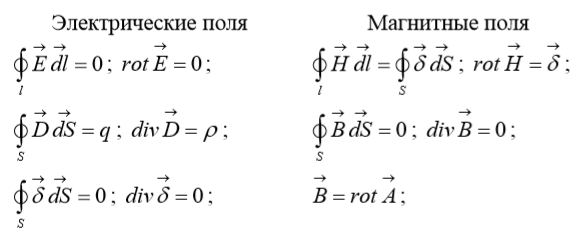
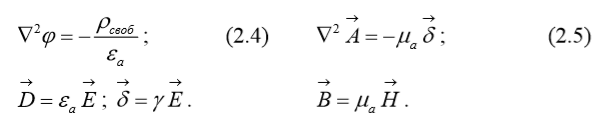
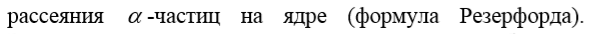
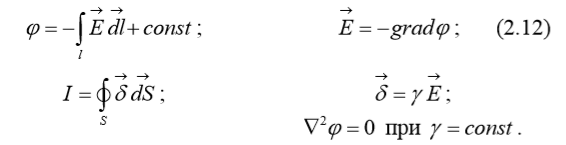
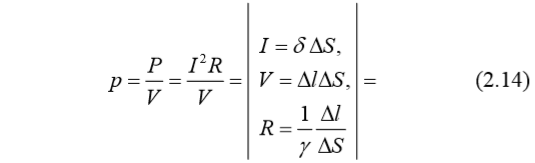
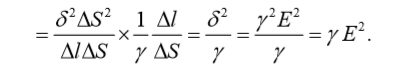
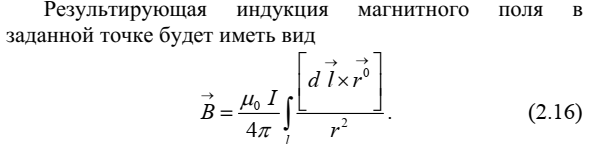
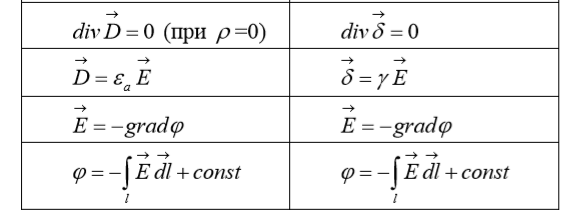
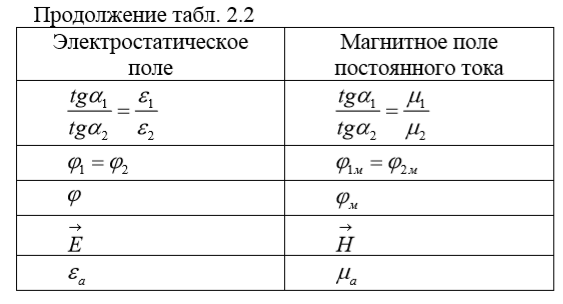
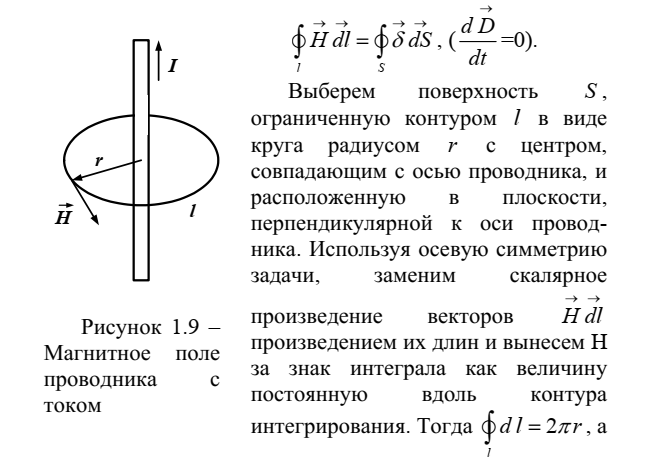
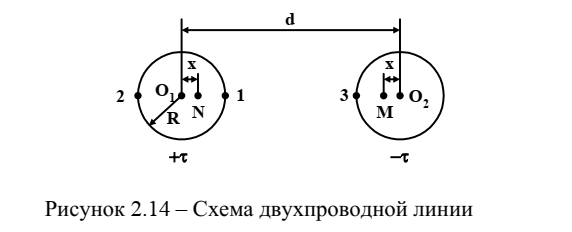
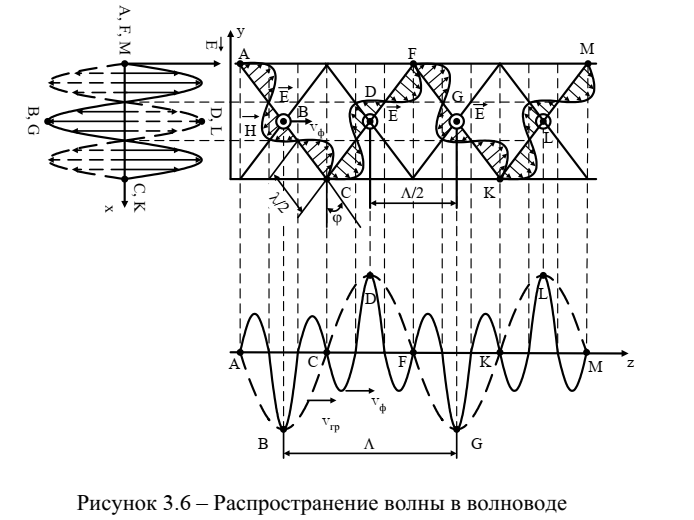
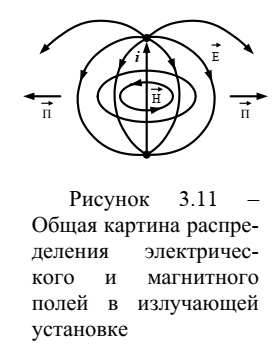
силовые линии магнитного поля.
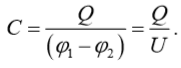
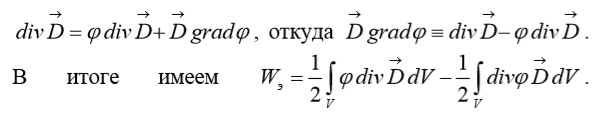
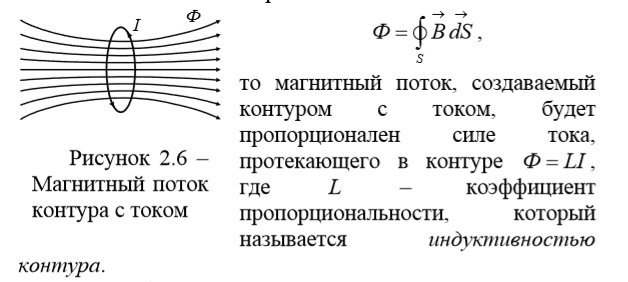
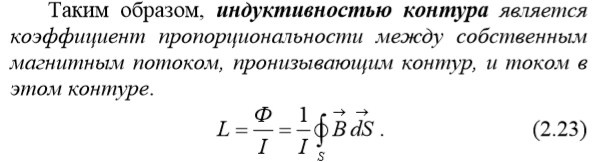
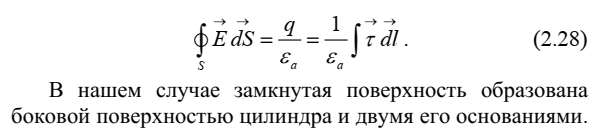
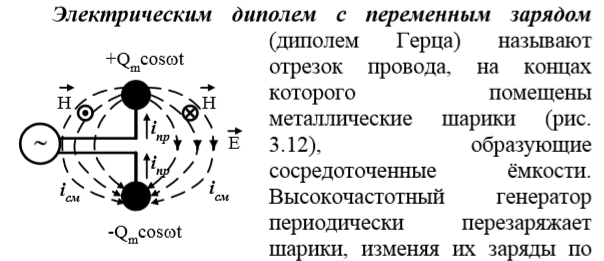
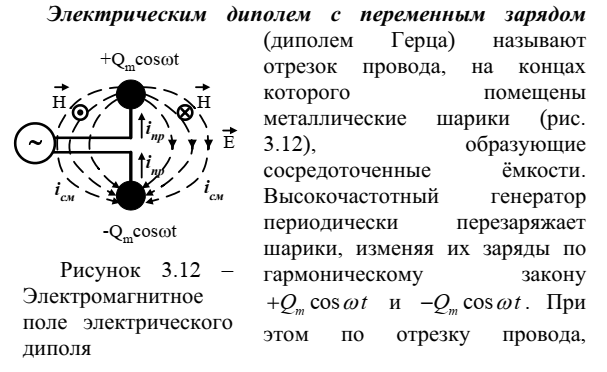
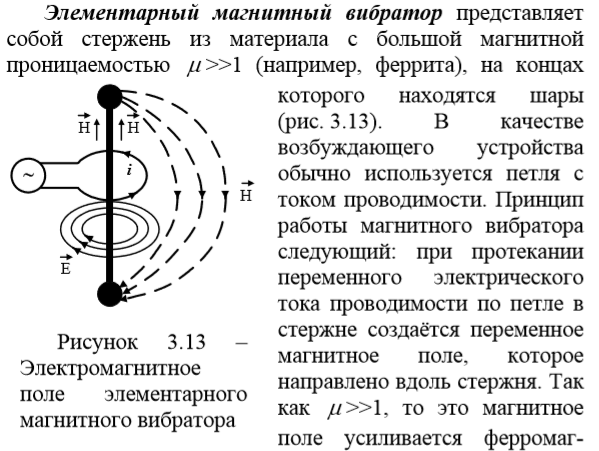
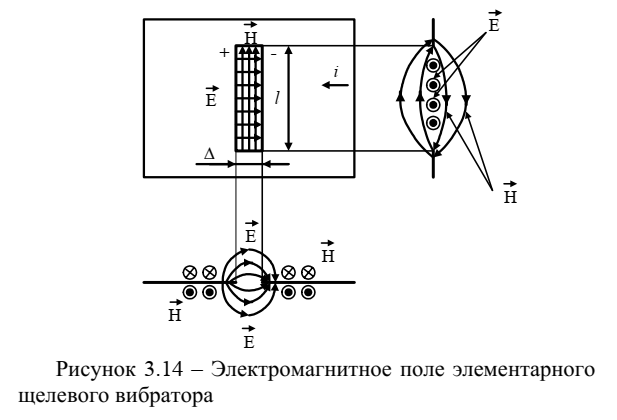
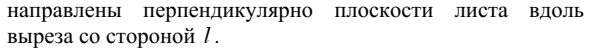
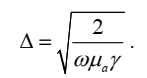
Источники электромагнитного поля
Среди основных источников ЭМИ можно перечислить:
1. Электротранспорт (трамваи, троллейбусы, поезда).
2. Линии электропередач (городского освещения, высоковольтные).
3. Электропроводка (внутри зданий, телекоммуникации).
4. Бытовые электроприборы.
5. Теле- и радиостанции (транслирующие антенны).
6. Спутниковая и сотовая связь (транслирующие антенны).
7. Радары.
8. Персональные компьютеры.
В качестве примера источников с высоким уровнем ЭМИ можно привести:
1. Высоковольтные ЛЭП.
2. Все виды электротранспорта, а также сопутствующая ему инфраструктура.
3. Теле- и радиовышки, а также станции передвижной и мобильной связи.
4. Установки для преобразования напряжения электрической сети (в частности, волны, исходящие от трансформатора или распределяющей подстанции).
5. Лифты и другие виды подъемного оборудования, где используется электромеханическая силовая установка.
К типичным источникам, излучающим низкоуровневые излучения можно отнести следующее электрооборудование:
1. Практически все устройства с ЭЛТ дисплеем (например: платежный терминал или компьютер).
2. Различные типы бытовой техники, начиная от утюгов и заканчивая климатическими системами;
3. Инженерные системы, обеспечивающие подачу электричества к различным объектам (подразумеваются не только кабель электропередач, а сопутствующее оборудование, например розетки и электросчетчики).