Лекция 11. Математическое доказательство
Понятие умозаключения. Виды умозаключений.
Правила вывода или схемы дедуктивных умозаключений.
Индуктивные умозаключения. Полная индукция. Неполная индукция.
Аналогия.
Способы математического доказательства.
Большую часть знаний об окружающем нас мире мы получаем с помощью рассуждений. Знание будет истинным, если оно получено путем правильного рассуждения, а таким считают рассуждение, построенное по правилам логики.
Рассуждения лежат в основе доказательства, без которого трудно представить математику. На сегодняшней лекции мы познакомимся с правилами, в соответствии с которыми строятся правильные рассуждения, познакомимся со структурой и способами доказательств, и взаимосвязях дедукции и индукции.
Понятие умозаключения. Виды умозаключений
В логике вместо термина «рассуждение» чаще используется (как его синоним) слово «умозаключение», им и будем пользоваться.
Определение. Умозаключение - эта форма мышления или логическое действие, в результате которого из одного или нескольких известных нам определенным образом связанных суждений получается новое суждение, в котором содержится новое знание.
Умозаключения бывают разные. Среди умозаключений, которые выполняют младшие школьники, изучая математику, выделяют:
- дедуктивные умозаключения;
- индуктивные умозаключения;
- рассуждения по аналогии.
Рассмотрим пример.
Пример 1. Ученику предлагается объяснить, почему число 23 можно представить в виде суммы 20 + 3. Он рассуждает: "Число 23 - двузначное. Любое двузначное число можно представить в виде суммы разрядных слагаемых. Следовательно, 23 = 20 + 3".
Первое и второе предложения в этом умозаключении - посылки, причем, одна посылка - общего характера - это высказывание "любое двузначное число можно представить в виде суммы разрядных слагаемых", а другая - частная, она характеризует только число 23 - "оно двузначное". Заключение - это предложение, которое стоит после слова "следовательно", - также носит частный характер, т.к. в нем речь идет о конкретном числе 23.
В примере 1 заключение логически следует из посылок, и мы не сомневаемся в его истинности. Такие умозаключения называют в логике дедуктивными.
Определение. Дедуктивным умозаключением называют умозаключение, в котором посылки и заключение находятся в отношении логического следования.
Если посылки дедуктивного умозаключения обозначить буквами А1, А2,...Аn, а заключение - буквой В, то схематично само умозаключение можно представить так:
А1, А2,...Аn 
В. Часто используют такую запись:
А1, А2,...Аn. Здесь черта заменяет слово "следовательно".
В
Замечание.
- В дедуктивных умозаключениях мысль движется от общего к частному.
- Дедуктивные умозаключения позволяют строить частные суждения из общих.
- В дедуктивном умозаключении при истинных посылках, истинно и заключение.
Определение. Индуктивное умозаключение - это такое умозаключение, в результате которого на основании знания об отдельных предметах данного множества (или об отдельных подмножествах данного множества) получается общий вывод, содержащий какое-либо знание обо всех предметах данного множества.
В начальном курсе математики выделяют полную и неполную индукцию.
Определение.Полная индукция – умозаключение, в правильности которого убеждаются, рассматривая все отдельные случаи (объекты, фигуры, числа), которые составляют конечное множество.
Утверждения, которые делаются на основе использования полной индукции, всегда правильные, так как полная индукция является методом доказательства.
Кроме полной индукции, в математике и в методике ее преподавания встречаются рассуждения по неполной индукции.
Определение. Неполная индукция – умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.
Является ли это умозаключение логически строгим? Конечно, нет. Верно ли, что такого типа умозаключениями нельзя пользоваться? Нет, так как такого типа умозаключения часто являются источником правильных гипотез, укрепляют веру в истинность утверждений, которые на определенном этапе обучения нельзя обосновать строго.
Например, построив по точкам графики нескольких линейных функций, учащиеся убеждаются, что графиком их является прямая линия. После этого по индукции делается вывод, что графиком какой–либо функции является прямая линия. Этот вывод правильный, хоть и имеет характер гипотезы, пока в аналитической геометрии не будет доказан.
Рассуждения по неполной индукции часто встречаются в начальном курсе обучения математике. Они являются как бы источником веры в правильность действий учителя и ученика. Приведем пример рассуждений, называемых неполной индукцией.
Пример 2. Один из приемов ознакомления младших школьников с переместительным законом умножения заключается в следующем. Используя различные средства наглядности, школьники вместе с учителем устанавливают, что 6∙3=3∙6, 5∙2=2∙5, 3∙7=7∙3. А затем, на основе полученных равенств, делают вывод: для всех натуральных чисел а и b верно равенство a∙b=b∙a.
В данном умозаключении посылками частного вида являются первые три равенства: в них утверждается, что для конкретных натуральных чисел выполняется такое свойство. Заключением является утверждение общего характера - переместительное свойство умножения натуральных чисел.
Очевидно, что ни один из приведенных аргументов не является логически достаточным для того, чтобы сделать вывод о справедливости переместительного закона умножения. Демонстрация конечного (и даже большого) количества числовых примеров не является достаточным аргументом для того, чтобы утверждать, что свойство справедливо для всех пар чисел.
Замечание. Часто рассуждения по неполной индукции приводят к неправильным выводам. Однако в методике преподавания начального курса математики они используются в тех случаях, когда вывод не вызывает сомнений и когда нет возможности обосновать правило или закон в полной мере. Таких случаев довольно много.
Еще одним важным видом умозаключений, используемых в математике, является аналогия.
Определение.Аналогия - умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Пример 3. При обучению делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значение выражения 12:4, следует узнать, на какое число надо умножить делитель 4, чтобы получить 12. Известно, что 4∙3=12. Значит, 12:4=3.
Затем учащимся предлагается, рассуждая также, найти, например, частное 8:4. И они сначала находят число, на которое надо умножить 4, чтобы получить 8. Получают число 2 и делают вывод - 8:4=2.
Далее, используя тот же способ рассуждений, находят частные 9:3, 20:5 и др.
Аналогия – достаточно эффектный механизм познания, умственный прием, используемый как в научных исследования, так и в обучении. Рассуждения по аналогии имеют следующую общую схему:
А обладает свойствами a и b;
В обладает свойствами a,
Возможно, В обладает свойством b.
Широко используется аналогия в обучении математике младших школьников. Аналогию можно использоватьдля:
- «открытия» новых свойств изучаемых объектов.
- установления отношений между данными объектами.
- для выводов о способе действия на основе изучения другого способа.
Аналогия часто приводит к неправильным выводам.
Приведем несколько типичных примеров ошибок, совершаемых учениками из-за неправильного применения рассуждений по аналогии.
В начальной школе известно, что действия сложения и умножения переместительны и сочетательны. Некоторые ошибки могут возникнуть из-за переноса этих свойств по аналогии на действия вычитания и деления. Например, 158-18-10=158-(18-10)=158-8=150. Здесь «незаконно» использовалось свойство сочетательности вычитания, которого у вычитания нет.
Если в математике ошибки по аналогии достаточно «безобидны», то в жизни это не так. Съев ягоду, похожую на хорошую, ребенок может отравиться.
Правила вывода или схемы дедуктивных умозаключений
Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению, в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?
В логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных умозаключений. Наиболее часто встречаются следующие:
- правило заключения;
- правило отрицания;
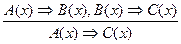- правило силлогизма.
Приведем примеры умозаключений, выполненных по этим правилам:
Правило заключения: Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.
Правило отрицания: Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, число 177 не оканчивается цифрой 5.
Правило силлогизма: Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то х кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.
В логике существуют различные способы проверки правильности умозаключений. Один из них состоит в использовании кругов Эйлера. Для этого сначала умозаключение записывают на теоретико-множественном языке, а посылки изображают на кругах Эйлера, считая их истинными. После чего выясняют, всегда ли при таких посылках истинно заключение. Если оказывается, что всегда, то говорят, что данное умозаключение дедуктивное. Если же возможен рисунок, из которого видно, что заключение может быть ложным, то говорят, что всякое умозаключение, выполненное по такой схеме, не является дедуктивным.
Покажем, что умозаключение, выполненное по правилу заключения, является дедуктивным. Сначала запишем это правило на теоретико-множественном языке.
Посылка 
может быть записана в виде ТА 
, где ТА и ТВ - множества истинности высказывательных форм А(х) и В(х). Частная посылка А(а) означает, что а 
ТВ. Все умозаключения, построенные по правилу заключения, записываются на теоретико-множественном языке так:
Изобразив на кругах Эйлера множества ТА и ТВ и обозначив элемент а 
, видим, что а 
, т.е. а а .