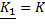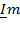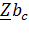Комплексные величины электрической цепи

Практическая работа №12

« Расчет неразветвленной цепи переменного тока символическим методом»

 

Цель: закрепить навыки расчета цепей переменного тока с применением комплексных чисел при последовательном соединении активных и реактивных сопротивлений.

Теоретические положения

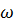Для определения в произвольный момент времени заданной частоты необходимо знать два числа, например амплитуду и начальную фазу (а также 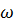), можно записать, что в любой момент времени

.

Однако вместо двух действительных чисел можно пользоваться одним комплексным числом. Применение комплексных чисел упрощает расчеты цепей переменного тока и находит широкое применение.

Комплексным числом или, короче, комплексом называется сумма числа и мнимого , представляющего собой квадратный корень из отрицательно числа или произведение действительного числа 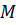и квадратного корня отрицательной единицы , называемой мнимой единицей и обозначаемой в электротехнике буквой .

Таким образом, комплексное число

 

. (1)

 

Действительное число графически изображают отрезком на оси абсцисс , которую называют осью действительных величин или, короче, действительной осью (рисунок 1). Например, заданное действительное положительное число 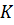изображено на рисунке 1 отрезком или вектором 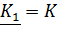на положительной полуоси действительных величин.

Таким образом, мнимая единица представляет собой поворотный множитель, при умножении на который вектор, изображающий действительное число 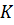, поворачивается на угол против направления движения часовой стрелки, т.е. в положительную сторону. Умножение на мнимого числа или в общем случае комплексного числа также приводит к повороту изображающего вектора на в том же направлении. Например, умножение на поворачивает изображающий вектор на угол в том же направлении, и вектор получается , изображающий отрицательное число , так как

;

Здесь принято во внимание, что по определению

 

Ось действительных величин 0	0 α +1 +j
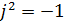
Рисунок 1 – Графическое изображение действительных и мнимых чисел	Рисунок 2 – Разложение вектора на составляющие, совпадающие по направлению с осями координат

 

Третье умноженье числ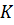а на дает отрицательное мнимое число

 

,

 

т.е.

 

и изображающий вектор вновь повернется на и займет положение на отрицательной полуоси мнимых величин – вектор 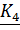на рисунке 1.

Четвертый поворот возвращает вектор в исходное положение, при этом

 

.

 

На рисунке 2 комплексное число изображено вектором , проекция которого на действительную ось равна его действительной части re , а проекция на мнимую ось – мнимой части Im ; таким образом, можно записать, что

 

, (2)

где и – обозначения действительной и мнимой составляющих.

Положительные полуоси действительных и мнимых величин обычно обозначают знаками «+1» и «+j», как и показано на рисунке 2 и последующих. Плоскость на которой изображаются комплексные величины или числа, называют комплексной плоскостью.

Векторы, изображающие комплексные величины, записывают с чертой снизу (, , , , ).

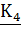Длина вектора или модуль вектора

 

. (3)

 

Угол α, образованный вектором и положительной полуосью действительных величин и называемый аргументом вектора , определяется через его тангенс:

 

. (4)

 

Положение вектора на комплексной плоскости определяется по знакам и или значению .

Итак, вектор, изображающий комплексную величину или число, определяется действительной мнимой частями или значениями модуля и аргумента.

Кроме рассмотренной алгебраической формы записи комплексных величин и чисел применяется еще тригонометрическая форма, при которой действительная и мнимая части комплекса (2) выражаются через модель и аргумент. Как видно на рисунке 2,

 

. (5)

 

Применяется еще третья – показательная форма комплексных величин. Комплексное число в показательной форме выражается произведением модуля и поворотного множителя

 

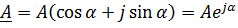(6)

 

Из (6) следует, что поворотный множитель (формула Эйлера)

 

, (7)

 

где и .

 

Поворотный множитель показывает, что вектор повернут относительно положительной полуоси действительных величин на угол α против направления движения часовой стрелки. Отрицательному значению угла α соответствует поворот вектора по часовой стрелке.

Так как показатель степени должен быть отвлеченным числом, то угол поворотного множителя должен выражаться в радианах. Однако ради большей наглядности допускается его условная запись в градусах.

Рассмотрим несколько характерных примеров вычислений с поворотным множителем, результаты которых полезно запомнить:

1) ;

2)

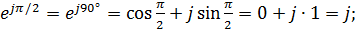
3) ;

4) .

 

Комплексные величины электрической цепи

Установлено, что мгновенное значение синусоидального тока или напряжения можно изображать проекцией вращающего вектора на неподвижную ось. Покажем теперь, что вращающиеся векторы, а следовательно, и изображаемые ими синусоидальные величины можно выражать комплексными числами.

Допустим, что требуется представить комплексом ток, амплитуда которого , а начальная фаза , т.е.

 

. (8)

 

Изобразим на комплексной плоскости под углом к положительной полуоси действительной величин вектор

 

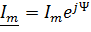(9)

 

длиной повернутый относительно оси действительных величин на угол (рисунок 3). Если этот вектор вращать в положительном направлении с угловой скоростью 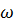, то мгновенное значение тока изобразиться проекцией вращающегося вектора на мнимую ось; это условно можно записать так:

 

.

0 Ѱ +1 ω +j i ωt

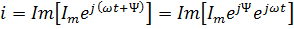Рисунок 3 Вектор тока на комплексной плоскости

Отмечено, что взаимное расположение векторов на векторной диаграмме с течением времени не изменяется; поэтому нет необходимости вращать векторы при изображении синусоидально изменяющихся величин на комплексной плоскости. Достаточно изобразить векторы в начальный момент времени, т.е. представить их комплексами. Например, ток (8) можно представить в символической записи (9).

Учитывая, что на векторных диаграммах обычно откладывают не амплитуды, а действующие значения синусоидальных величин, комплексное значение тока, или, короче, комплексной тока, запишем в виде

 

(10)

 

(отсутствие индекса указывает на то, что записано действующее значение комплексной величины).

Аналогично выполняется символическая запись напряжения.

Если

, (11)

 

то комплекс напряжения

 

. (12)

 

Частное от деления комплекса напряжения на выводах цепи (ветви) на комплекс тока называется комплексным сопротивлением цепи и обозначается прописной буквой , т.е.

(13)

или

, (14)

где - активное сопротивление; – реактивное сопротивление и – полное сопротивление.

Придав выражению (13) другой вид, получим

 

(15)

Закон Ома в комплексной форме.

Например, для последовательной схемы замещения катушки индуктивности (рисунок 4) при токе напряжение , где , или в комплексной форме

,

R

i

u

L

Рисунок 4 – Эквивалентная схема цепи с сопротивлением

и индуктивностью

 

а комплексное сопротивление

 

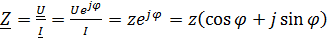; (16)

 

так как для цепи с индуктивностью , то

 

. (17)

 

0 +1 φ>0 +j	0 +1 φ>0 +j
Рисунок 5 – Треугольник сопротивлений - цепи	Рисунок 6 – Векторная диаграмма - цепи

 

Комплексное сопротивление и его действительная и мнимая составляющие могут быть представлены на комплексной плоскости (рисунок 5) в виде треугольника сопротивлений.

Модуль комплексного сопротивления, обозначенный строчной буквой z, определяется по формуле:

 

,

 

а аргумент – через его синус или тангенс:

 

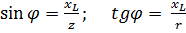, т.е. .

 

Из (15) напряжения на выводах цепи:

 

.

 

Первое слагаемое этого выражения представляет собой комплексное напряжение на активном сопротивлении. Это напряжение совпадает по фазе с током (рисунок 6), и, естественно, комплексы и имеют одинаковый аргумент, равный нулю. Второе слагаемое – комплексное напряжение на индуктивности , аргумент которого равен (как уже известно, напряжение на индуктивности опережает по фазе ток на ). Таким образом, множитель в выражении ясно показывает, что на индуктивности между напряжением и током имеется сдвиг фаз .

r

u

С

i

Рисунок 7 – Цепь с сопротивлением и емкостью

 

Для неразветвленной цепи с активным сопротивлением и емкостью (рисунок 7) при напряжение , где , комплексное сопротивление

,

 

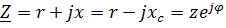где т.е. .

 

Треугольник сопротивлений показан на рисунке 8.

0 +1 φ<0 +j r	0 +1 φ<0 +j I
Рисунок 8 Треугольник сопротивлений rC - цепи	Рисунок 9 – Векторная диаграмма rC – цепи
0 +1 φ>0 +j ɡ	0 +1 φ<0 +j ɡ
Рисунок 10 – Треугольник проводимостей rL - цепи	Рисунок 11 - Треугольник проводимостей rC – цепи

 

Напряжение на емкости

 

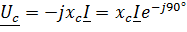
Отстает по фазе от тока на 90° (рисунок 9). Напряжения на выводах цепи

 

.

 

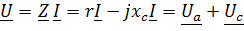Следует обратить внимание на то, что комплекс не зависит от выбора начальной фазы тока или напряжения. Например, для – цепи при любой начальной фазе тока напряжение будет опережать ток цепи на угол φ, тангенс которого равен отношению . Действительно, выбрав у тока начальную фазу Ѱ (8), т.е. приняв 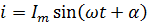, запишем напряжение (11) , которое должно по-прежнему опережать ток на тот же угол φ, так как имеет то же значение, что и при нулевой начальной фазе. Следовательно, и комплексное сопротивление

 

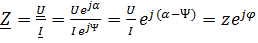. (18)

 

При расчетах разветвленных цепей часто вводят комплексную проводимость – величину, обратную комплексному сопротивлению:

 

, (19)

 

где – активная проводимость; – реактивная проводимость.

Например, для последовательной – цепи комплексная проводимость (рисунок 10)

.

 

где активная проводимость и индуктивная определяются по известным уже выражениям

; ; .

 

Модуль комплексной проводимости можно определить по известной формуле

 

,

 

а аргумент – через его синус или тангенс:

 

,

 

откуда видно, что , т.е. напряжение опережает по фазе ток.

Для последовательной 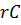– цепи комплексная проводимость (рисунок 11)

 

,

где активная проводимость и емкостная определяются по известным уже выражениям

; = и .

 

Модуль комплексной проводимости

 

,

 

а аргумент определяется через синус или тангенс:

 

; .

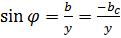Откуда следует, что , т.е. напряжение опережает по фазе напряжение.

Наконец, для – цепи можно написать

 

;

,

где активная и реактивная проводимости

 

; ;

;

 

угол при или при ;

угол при или при .

 

Пример 1. Неразветвленная цепь с активным сопротивлением Ом и емкостным сопротивлением 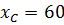Ом находится под напряжением В. Определить ток в цепи.

 

Решение. Комплексное сопротивление

Ом;

модуль и аргумент этого сопротивления

Ом;

; .

То же сопротивление в показательной форме

Ом.

Ток в цепи

А;

А.

 

Если ток и напряжение в цепи выражены в комплексной форме, то активную и реактивную мощности цепи определяют, умножая комплексное напряжение на сопряженный комплексный ток.

Допустим, что , напряжение , т.е. вектор напряжения опережает вектор тока на угол , что при положительном значении угла соответствует индуктивной нагрузке.

Произведение комплекса напряжения и сопряженного комплекса тока представляет мощность в комплексной форме, или короче, комплексную мощность. Действительно,

. (20)

Таким образом, действительная часть полученного комплекса выражает активную мощность, а мнимая – реактивную мощность цепи. При емкостной нагрузке, т.е. при , мнимая часть комплексной мощности имеет отрицательный знак ().

Пример 2. Определить активную и реактивную мощности цепи, если ток 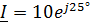А, напряжение В.

Решение.

; ; .
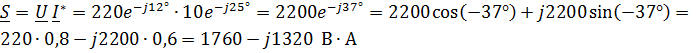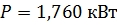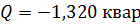