Для узла электрической цепи переменного тока по первому закону Кирхгофа сумма мгновенных значений токов, направленных к узлу, равна сумме мгновенных значений токов, направленных от узла. То же самое правило справедливо и при записи токов в комплексной форме.
Например, для узла А (рисунок 12) получим первый закон Кирхгофа в комплексной форме:
 , (21)
, (21)
или сумма комплексных токов, направленных к узлу, равна сумме комплексных токов, направленных от него.
|
|
|
| Рисунок 12 – Узел электрической цепи
| Рисунок 13 – Схема к примеру 3
|
Считая токи, направленные от узла положительными, а токи, направленные к узлу, отрицательными, можно написать и так
 , (22)
, (22)
или в общем виде
 , (23)
, (23)
т.е. алгебраическая сумма комплексных токов в узле равна нулю. Уравнение (23) по виду ничем не отличается от уравнения ( ), выражающего то же правило для цепи постоянного тока. Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках.
), выражающего то же правило для цепи постоянного тока. Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках.
Приписав ЭДС и токам, совпадающим по направлению с направлением обхода контура, знак плюс, а несовпадающим – минус, получим при комплексной записи для любого замкнутого контура
 , (24)
, (24)
где к числу ЭДС 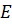 относится только ЭДС источников, так ка ЭДС самоиндукции учитываются соответствующими падениями напряжения (
относится только ЭДС источников, так ка ЭДС самоиндукции учитываются соответствующими падениями напряжения ( ). Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений.
). Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений.
Последнее уравнение называется вторым законом Кирхгофа в комплексной форме. Оно также совпадает по виду с уравнением для цепи постоянного тока ( ). Как и в цепях постоянного тока, для записи уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов.
). Как и в цепях постоянного тока, для записи уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов.
Пример 3. Определить ток  в неразветвленной части цепи (рисунок 13), если токи в ветвях
в неразветвленной части цепи (рисунок 13), если токи в ветвях  А;
А;  А;
А;  А.
А.
Решение. Определим комплексы токов в ветвях:
 А;
А;
 А;
А;
 А.
А.
Комплекс тока в неразветвленной части цепи
 А.
А.
Мгновенное значение тока  ,
,
где 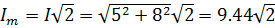
 ,
,
таким образом,  А.
А.
Введя комплексную форму записи для всех параметров и величин, определяющих режим цепи переменного тока, можно геометрические операции над векторами заменить алгебраическими над изображающими их комплексами, а все соотношения и законы цепей постоянного тока формально применять к расчету цепей переменного тока.
В частности, при комплексной форме записи известные методы расчета цепей постоянного тока (метод контурных токов, метод узловых потенциалов, метод преобразования и др.) применимы и для расчета цепей переменного тока.
Для решения системы уравнений с большим числом неизвестных токов применяют ЭВМ, обеспеченные типовыми программами. Для расчетов режимов относительно простых цепей, рассмотренных в следующих параграфах, целесообразно применение микрокалькуляторов.
Практическая работа №12
« Расчет неразветвленной цепи переменного тока символическим методом»
Цель: закрепить навыки расчета цепей переменного тока с применением комплексных чисел при последовательном соединении активных и реактивных сопротивлений.
Ход работы.
1. Начертить схему согласно своему варианту (таблица 1).
2. Используя значения таблицы 1, записать исходные данные согласно своему варианту.
3. Рассчитать напряжения на всех участках, используя символический метод расчета.
4. Силу тока цепи  .
.
5. Активную  , реактивную
, реактивную  и полную
и полную 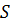 мощности цепи.
мощности цепи.
6. Начертить в масштабе векторную диаграмму напряжений.
Исходные данные. Цепь переменного тока со смешанным соединением сопротивлений содержит активные и реактивные сопротивления, величины которых заданы в таблице 1, Причем  ,
,  ,
, 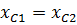 . К цепи приложено напряжение
. К цепи приложено напряжение  .
.
| Ва-ри-ант
| r1
Ом
| r2
Ом
| r3
Ом
| xC1
Ом
| xC2
Ом
| xC3
Ом
| xL1
Ом
| xL2
Ом
| xL3
Ом
| С1
мкФ
| С2
мкФ
| С3
мкФ
| L1
Гн
| L2
Гн
| L3
Гн
| f
Гц
| P
Вт
| Q
ВАр
| S
ВА
| I
А
| U
В
| Схема
|
|
|
|
|
|
| -
| -
|
| -
| -
| -
|
| -
| -
| 0.03
| -
|
| -
| -
| -
| -
| 100
|
|
|
|
|
| -
|
|
| -
|
| -
| -
| 35.38
| -
|
| -
| 0.02
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
| -
| -
| -
|
| -
| -
| 0.02
| -
|
| -
| -
| -
| -
| 200
|
|
|
|
|
|
| -
| -
| -
|
|
| -
| 79.6
|
| -
| -
| -
| 0.007
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
| -
|
|
| -
| -
|
| -
| -
| -
| 0.02
|
| -
| -
| -
| -
|
|
|
|
|
| -
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.01
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.007
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
| -
| -
| -
|
| -
| -
|
|
| -
| -
| 0.01
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
| -
| -
| -
|
|
| -
|
|
| -
| -
| -
| 0.008
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
|
|
|
| 6.3
| -
|
| -
| -
| -
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.004
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
| -
| -
| -
|
| -
| -
| 0.03
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
|
|
| -
|
| -
| -
| -
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
| -
|
| -
|
| -
| -
| 75.8
| -
|
| -
| 0.001
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.003
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.003
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
| -
| -
| -
| -
|
| -
| 0.002
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
| -
| -
| -
|
| -
| -
| 0.03
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
| -
|
| -
|
| -
| -
| 0.04
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
| -
|
| -
| -
|
|
|
| -
| -
| 0.03
| -
| -
|
| -
| -
| -
| -
|
|
|
|
|
| -
| -
|
| -
|
|
| -
|
| -
|
| -
| -
| 0.02
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
| -
|
|
|
| -
| -
|
| -
| -
| -
| 0.03
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
| -
|
| -
|
| -
| -
|
| -
| -
| -
| 0.02
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
| -
|
|
| -
| -
|
| -
| -
| -
| 0.006
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.01
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
|
|
|
|
| -
| -
| -
| -
| -
| -
| 0.04
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
| -
| -
| -
|
| -
| -
| 0.02
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
|
|
| -
| -
|
|
| -
| -
|
| -
| -
| -
| 0.008
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
| -
| -
| -
| -
|
| -
| 0.02
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.003
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
| -
|
|
| -
| -
|
| -
| -
| -
| 0.02
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
| -
|
|
|
| 6.3
| -
|
| -
| -
| -
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.003
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
| -
|
| -
| -
|
|
|
| -
| -
| 0.03
| -
| -
|
| -
| -
| -
| -
|
|
|
|
|
|
| -
|
|
| -
|
|
| -
| -
| -
|
| -
| -
| 0.003
|
| -
| -
| -
| -
|
|
|
Содержание отчета
1. Тема.
2. Цель.
3. Ход работы.
4. Контрольные вопросы.
5. Литература.
Контрольные вопросы.
1. Какие формы записи комплексных чисел вам известны?
2. Записать формулу теоремы Эйлера.
3. Какая форма комплексных чисел наиболее удобна для их сложения и вычитания?
4. Какая форма комплексных чисел наиболее удобна для их умножения и деления?
5. Какие комплексные числа называются сопряженными
6. Если напряжение задано комплексным числом, как определить его мгновенное значение?
 , (21)
, (21) , (22)
, (22) , (23)
, (23) ), выражающего то же правило для цепи постоянного тока. Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках.
), выражающего то же правило для цепи постоянного тока. Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках. , (24)
, (24)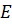 относится только ЭДС источников, так ка ЭДС самоиндукции учитываются соответствующими падениями напряжения (
относится только ЭДС источников, так ка ЭДС самоиндукции учитываются соответствующими падениями напряжения ( ). Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений.
). Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений. ). Как и в цепях постоянного тока, для записи уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов.
). Как и в цепях постоянного тока, для записи уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов. в неразветвленной части цепи (рисунок 13), если токи в ветвях
в неразветвленной части цепи (рисунок 13), если токи в ветвях  А;
А;  А;
А;  А.
А. А;
А; А;
А; А.
А. А.
А. ,
,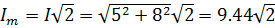
 ,
, А.
А. .
. , реактивную
, реактивную  и полную
и полную 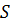 мощности цепи.
мощности цепи. ,
,  ,
, 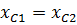 . К цепи приложено напряжение
. К цепи приложено напряжение  .
.








