Оценка эффективности рекламы

Аппроксимация данных. Подбор формул со многими неизвестными

Использование линии тренда графиков Excel – наиболее наглядный и информативный способ восстановления зависимости и исследования связи между двумя переменными. Для зависимостей со многими неизвестными подбор формул можно выполнить несколькими способами:

- с помощью функций из группы Статистические - ЛИНЕЙН и ЛГРФПРИБЛ.

- функции ТЕНДЕНЦИЯ и РОСТ – для вычисления значений аппроксимирующей функции в диапазоне наблюдения;

- инструмент для подбора формул со многими неизвестными Регрессия, входящий в Пакет анализа (Данные – Анализ данных…).

Функции ЛИНЕЙН и ТЕНДЕНЦИЯ применяют для аппроксимации экспериментальных данных линейными зависимостями вида y=b+a₁x₁+a₂x₂+…+a_nx_n.

Функции ЛГРФПРИБЛ и РОСТ применяют для аппроксимации экспериментальных данных нелинейными (показательными) зависимостями вида

Функции ЛИНЕЙН и ЛГРФПРИБЛ возвращают массив с т.н. регрессионной статистикой, который содержит вычисленные значения параметров (b,a₁,a₂,…a_n), коэффициент детерминации R ² и другие характеристики аппроксимирующей функции.

 

Рассмотрим пример оценивания значений функции y по трем переменным: х1, х2, х3, предполагая, что между каждой переменной х1, х2, х3 и зависимой переменной y существует линейная зависимость. Полученные в результате опыта (эксперимента) данные занесены в приведенную ниже таблицу.

 

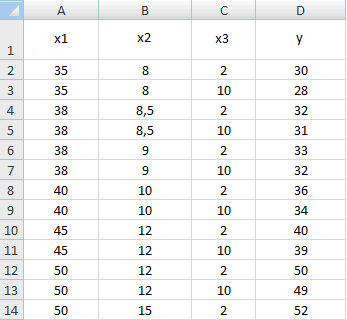
Необходимо подобрать формулу для вычисления эмпирических значений y и вычислить значение y с данными: х1 = 42, х2 = 11, х3 = 5.

Последовательность действий для решения задачи:

1. Заведите приведенную таблицу Excel в ячейки A1:D14.

2. Выделите диапазон ячеек B17:E21 (рис.2) для сохранения результатов вычислений функции ЛИНЕЙН – массива регрессионной статистики.

3. Вызовите мастер функций, выберите статистическую функцию ЛИНЕЙН и заполните параметры функции как на рис.1. Параметр Изв_знач_y содержит диапазон D2:D14, т.е. известные значения y. Параметр Изв_знач_х содержит диапазон A2:C14, т.е. известные значения х. Параметр Стат=1 - для получения дополнительной статистики.

 

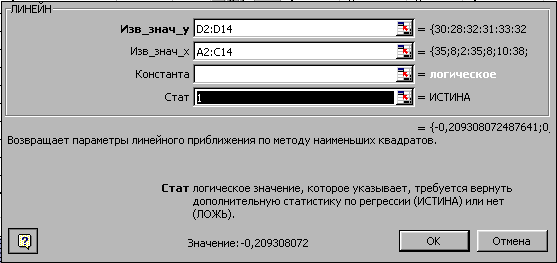
Рис. 1

 

4. После нажатия ОК встаньте на строку формул и нажмите Ctrl+Shift+Enter. В результате должен получиться массив значений, показанный на рис.2.

Искомые коэффициенты выделены на рисунке (подробнее см. справку F1). Коэффициент детерминации R² =0.9725 вполне удовлетворителен (близок к единице).

Таким образом, аппроксимирующая формула имеет вид:

Y = 1,36* х1 + 0,1* х2 – 0,21* х3 – 19,27

 

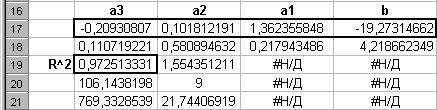
Рис. 2

 

5. С использованием полученной формулы вычислите значение функции y при х1 = 42, х2 = 11, х3 = 5, записав самостоятельно в любую ячейку формулу для автоматического расчета. Результат расчета: y = 37.9.

 

Использование функции ТЕНДЕНЦИЯ покажем на этом же примере для расчета значений y при различных вариантах данных X (рис.3).

 

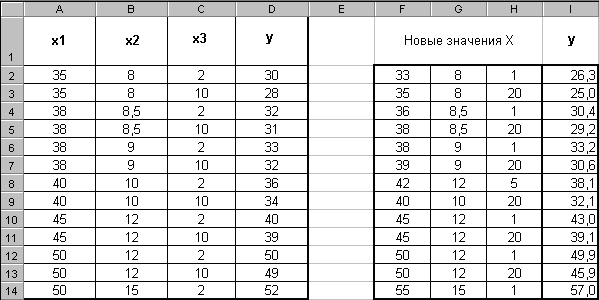
Рис. 3

 

Новые значения Х, для которых надо рассчитать y, введите в ячейки F2:H14.

Выделите диапазон I2:I14 для записи в него рассчитываемых значений y.

Вызовите мастер функций и функцию ТЕНДЕНЦИЯ. Параметры функции заполните как на рис.4. Параметр Нов_знач_х содержит диапазон F2:H14, т.е. новые значения x.

После нажатия ОК встаньте на строку формул и нажмите Ctrl+Shift+Enter. В результате диапазон I2:I14 будет заполнен рассчитанными значениями y (рис.3).

 

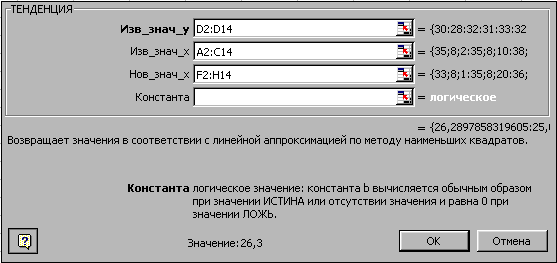
Рис. 4

Оценка эффективности рекламы

 

Подобрать формулу для вычисления процента увеличения оборота при различных затратах на рекламу. Экспериментально известны проценты увеличения оборота при затратах в 5, 10, 15, 20 тыс.$ в 3-х масс-медиа - на телевидении, радио и в прессе:

 

	5 тыс. $	10 тыс. $	15 тыс. $	20 тыс. $
1. TV	28%	43%	61%	95%
2. Радио	15%	24%	34%	50%
3. Пресса	6%	9%	13%	20%

 

Кроме этого, надо вычислить процент увеличения оборота при затратах на рекламу в прессе 2 тыс.$ и на телевидении 22 тыс.$. Дополнительно вычислите проценты при затратах во всех масс-медиа 2, 17 и 25 тыс.$.

 

Для решения задачи в первую очередь следует правильно разместить данные – рис.5.

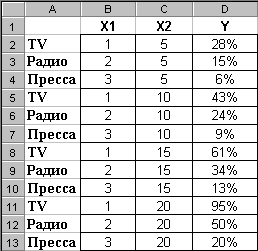
Рис. 5

 

Затем вычислите массив с регрессионной статистикой функцией ЛИНЕЙН: выделите диапазон ячеек F2:H6 и проделайте известные из предыдущего примера действия. В итоге должен получиться массив:

 

 

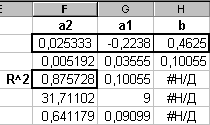
Как видно, коэффициент детерминации R ²=0.8757 недостаточно удовлетворителен.

Поэтому выполните подбор формулы с помощью функции для нелинейных зависимостей ЛГРФПРИБЛ: выделите диапазон ячеек F9:H13 и проделайте известные из предыдущего примера действия. В итоге должен получиться массив:

 

 

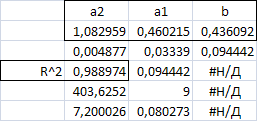
В этом случае коэффициент детерминации R ²=0.989 вполне удовлетворителен и можно записать искомую аппроксимирующую формулу показательного типа (т.к. использована функция ЛГРФПРИБЛ):

Y = 0,44 * 0,46^х1 * 1,08^х2

 

Теперь вычислите проценты увеличения оборота по условию задачи: введите формулы и не забудьте установить процентный формат отображения значений в ячейках:

 

Пресса, 2 тыс. $	5,0%	=H9*G9^3*F9^2
TV, 22 тыс. $	115,9%	=H9*G9^1*F9^22

 

Вычислите проценты для всех масс-медиа при затратах 2, 17 и 25 тыс.$. Подготовьте новые данные X в колонках K и L как на рис.6.

Для вычисления значений Y используем функцию РОСТ, поскольку известно, что зависимость нелинейная, показательная. Выделите диапазон ячеек M2:M10 и введите функцию РОСТ; заполнение параметров функции показано на рис.7.

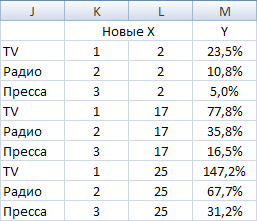
Рис. 6

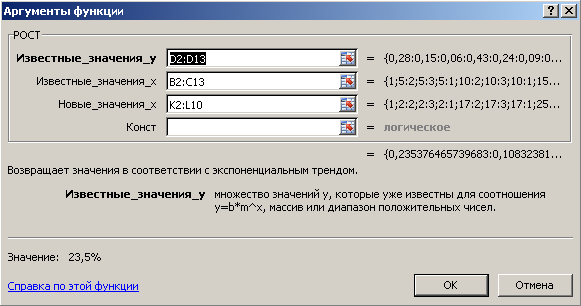
Рис. 7