В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа,
Криволинейной трапецией называется плоская фигура, ограниченная осью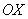 
, прямыми 
, 
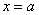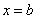и графиком непрерывной на отрезке 
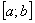функции 
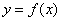, которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:
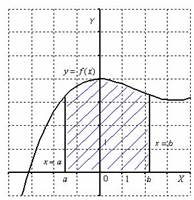
Тогда площадь криволинейной трапеции численно равна определенному интегралу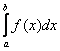 
. У любого определенного интеграла (который существует) есть очень хороший геометрический смысл. Определенный интеграл – это число. А С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ. То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
Пример 1 Вычислить площадь фигуры, ограниченной линиями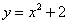 
, 
, 
, 
.
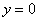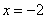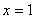Первый и важнейший момент решения – построение чертежа.
Выполним чертеж (обратите внимание, что уравнение 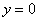задает ось ):
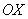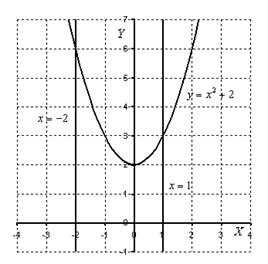Решение: на отрезке 
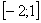график функции 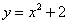расположен над осью 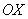, поэтому:
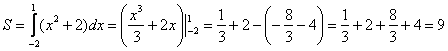Ответ: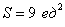 
Пример 2 Вычислить площадь фигуры, ограниченной линиями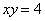 
, 
, 
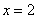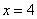и осью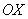
Решение:
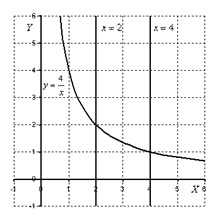
На отрезке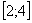 
график функции 
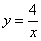расположен над осью 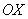, поэтому:
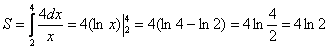Ответ: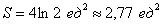 
Что делать, если криволинейная трапеция расположена под осью ?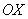
Пример 3 Вычислить площадь фигуры, ограниченной линиями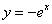 
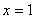, и координатными осями.
Решение: Выполним чертеж:
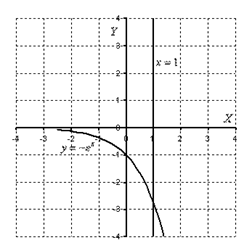Если криволинейная трапеция расположена под осью 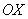(или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле: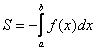 
В данном случае:
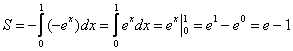Ответ: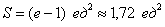 
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
Пример 4 Найти площадь плоской фигуры, ограниченной линиями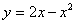 
, 
.
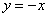Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы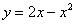 
и прямой 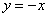. Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение: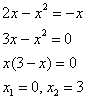 
Значит, нижний предел интегрирования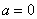 
, верхний предел интегрирования 
.
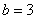Этим способом лучше, по возможности, не пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Выполним чертеж:
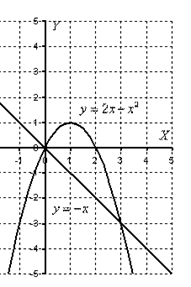
А теперь рабочая формула: Если на отрезке 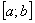некоторая непрерывная функция 
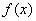больше либо равна некоторой непрерывной функции 
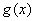, то площадь фигуры, ограниченной графиками данных функций и прямыми 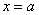, , 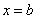можно найти по формуле: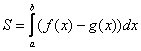 
Здесь уже не надо думать, где расположена фигура – над осью или под осью, важно, какой график ВЫШЕ (относительно другого графика), а какой – НИЖЕ.
В рассматриваемом примере очевидно, что на отрезке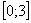 
парабола располагается выше прямой, а поэтому из 
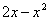необходимо вычесть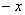 
Искомая фигура ограничена параболой 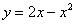сверху и прямой 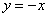снизу.
На отрезке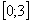 
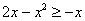, по соответствующей формуле:
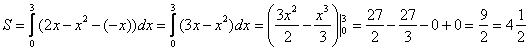
Ответ: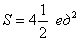 
Пример 5 Найти площадь фигуры, ограниченной линиями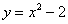 
, 
.
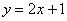Выполним чертеж:
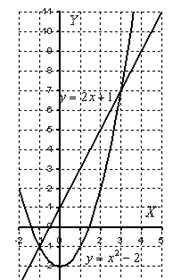
На отрезке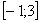 
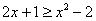, по соответствующей формуле:
Ответ: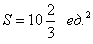 
Пример 6 Найти площадь фигуры, ограниченной линиями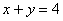 
, 
.
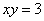Выполним чертеж.
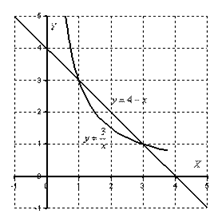
На отрезке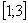 
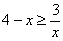, по соответствующей формуле:
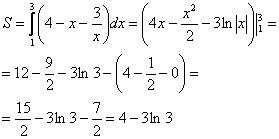
Ответ: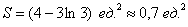 
Пример 7 Вычислить площадь фигуры, ограниченной линиями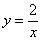 
, 
, , 
.
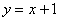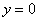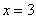Сначала выполним чертеж:
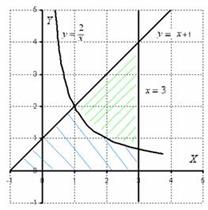
Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке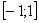 
над осью 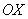расположен график прямой ;
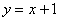2) На отрезке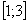 
над осью 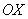расположен график гиперболы .
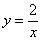Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:
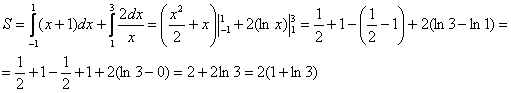
Ответ: 