Перестановка 
называется автоморфизмом графа G, если 
тогда и только тогда, когда 
. Как известно, множество всех автоморфизмов графа G относительно композиции преобразований образует группу Aut(G). Кроме того, каждый автоморфизм 
графа G индуцирует перестановку 
на EG по правилу: 
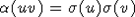для любого . Целью данного параграфа будет доказательство изоморфности групп Aut(G) и SG посредством определенного здесь соответствия " индуцирует 
".
Сначала несколько вспомогательных утверждений.
Лемма 1. Пусть 
. Вершины xe1 и xe2 многогранника MP(G) смежны тогда и только тогда, когда ребра e1 и e2 смежны в G.
Доказательство. Вершины xe1 и xe2 одновременно удовлетворяют (|EG|-2) линейно независимым уравнениям xe=0, 
, каждое из которых определяет опорную к MP(G) гиперплоскость. Следовательно, xe1 и xe2 принадлежат двумерной грани многогранника MP(G), которую можно определить опорной гиперплоскостью 
. Помимо вершин xe1, xe2 и 0 на этой грани может лежать только вершина 
(если и только если 
). При этом очевидно, что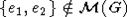 
тогда и только тогда, когда вершины xe1, xe2 смежны в MP(G). И наконец, ясно, что условие 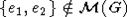эквивалентно смежности ребер e1 и e2.
Лемма 2. Пусть 
. Ребра смежны в G, если и только если ребра 
и 
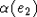смежны в G.
Доказательство. Следует из леммы 1.
Основываясь на том, что множество всех перестановок на EG является конечной группой, легко показать, что если для данной перестановки образы смежных в G ребер смежны, то и прообразы смежных ребер тоже смежны.
Следующая лемма играет важную роль при построении изоморфизма групп Aut(G) и SG.
Лемма 3. Если образы смежных в G ребер при перестановке смежны в G, то для любой 
существует такая вершина 
, что 
.
Доказательство. Для обозначим 
, p>1. Предположим, что ребра образа 
не имеют общей вершины. Тогда среди ребер 
, 
, есть несмежные, либо 
является циклом длины 3. В первом случае получаем противоречие с условием теоремы, ибо uui, 
, попарно смежны. Второй случай рассмотрим подробнее.
Пусть p=3 и 
, 
и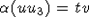 
. Так как G связен и |VG|>4, то существует вершина 
, которая смежна с какой-либо из вершин u1,u2,u3, - скажем, с u1. Так как uu1 и u1s смежны, то vw и 
тоже смежны. При этом если они смежны по вершине v, то получаем смежность ребер и 
и, как следствие, - смежность ребер u1s и uu3, что не так. Если же vw и смежны по вершине w, то аналогично получаем смежность ребер u1s и uu2, что также противоречит выбору вершины s. Следовательно, при p=3 ребра не могут образовывать цикла.
Итак, если не висячая вершина, то для нее существует такая , что 
. Из условия сохранения смежности ребер и взаимнооднозначности перестановки вытекает, что это включение является равенством, то есть 
. Нетрудно увидеть, что это равенство выполняется и для висячих вершин графа G.
Теперь, основываясь на лемме 3, определим соответствие правилом: 
, если и только если 
, где - перестановка на EG, сохраняющая смежность ребер. Легко заметить, что является перестановкой. Покажем, что она сохраняет смежность вершин графа G. Действительно, всякое ребро можно представить как пересечение множеств 
и 
. Следовательно,
Ясно, что последнему пересечению может принадлежать только ребро 
.
Таким образом, доказано, что является автоморфизмом графа G, причем индуцирует перестановку .
Проведенные рассуждения сформулируем в виде теоремы.
Теорема 1. Перестановка 
индуцирована некоторым автоморфизмом графа G тогда и только тогда, когда образы смежных в G ребер при перестановке смежны.
Переход к группе SG осуществляется с помощью следующего результата.
Теорема 2. Перестановка на множестве EG индуцирована некоторым автоморфизмом графа G тогда и только тогда, когда .
Доказательство. Достаточность. В силу леммы 2, образы смежных в G ребер при перестановке смежны. Значит, по теореме 1, индуцирована некоторым автоморфизмом графа G.
Необходимость. По теореме 1, образы смежных ребер смежны. Покажем, что 
для любого 
. Действительно, если 
смежны, то 
и 
тоже смежны, чего быть не может, ибо и принадлежат H.
Теорема 2 позволяет заключить, что соответствие " индуцирует ", определенное в начале данного параграфа, является отображением группы Aut(G) на SG. Обозначим его через 
.
Теорема 3. Соответствие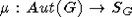 
является изоморфизмом групп Aut(G) и SG.
Доказательство. Действительно, если 
и 
- два различных автоморфизма, то существует такая вершина , что 
. Пусть 
, i=1,2. Ясно, что 
. Следовательно, 
. Тем самым доказана взаимнооднозначность соответствия .
Далее, полагая 
и 
, получим
Теорема доказана.
Итак, суммируя полученные результаты, получаем изоморфность группы линейных симметрий многогранника паросочетаний и группы автоморфизмов соответствующего графа.
В заключение отметим, что аналогичные результаты о симметриях многогранника матроида получены О.В.Червяковым в работе [2].
Список литературы
Емеличев В.А. и др. Лекции по теории графов. М.:Наука, 1990.
Червяков О.В. Линейные симметрии и автоморфизмы матроида // Фунд. и прикл. матем.: Сб. науч. тр. Омск: ОмГУ, 1994. C.81-89.
Edmonds J. Maximum matching and a polyhedron with 0,1-vertices // Jornal of Research of the National Bureau of Standards B, 1965. P.125-130.
Chvatal V. On certain polytopes associated with graphs // Journal of Combinatorial Theory (B). 1975. N 18. P. 138-154.