Методические советы. Ознакомиться с общим способом построения линии пересечения одной поверхности другой, из которых хотя бы одна кривая. Обратить внимание, что при построении точек линии пересечения поверхностей вначале находят те точки, которые называются характерными или опорными.
Изучить метод применения вспомогательных секущих! плоскостей. Затем перейти к изучению метода применения вспомогательных сфер с постоянным и переменным центром.
В заключение ознакомиться с некоторыми особыми случаями пересечения одной, поверхности другою.
Вопросы для самопроверки
1. Какая категория точек линии пересечения поверхностей относится к опорным?
2. С определения каких точек следует начинать построение линии пересечения поверхностей и почему?
3. По какому правилу следует соединять построенные точки линии пересечения кривых поверхностей?
4. При каких условиях поверхности вращения (например, сфера и конус, сфера и цилиндр) пересекаются по окружностям?
КОНТРОЛЬНАЯ РАБОТА 1 (листы 1, 2)
Лист 1
Задача 1. Построить линию пересечения треугольников ABC и EDK и показать ее видимость в проекциях. Пример выполнения листа приведен на рисунке 1. Указания к решению задачи. В левой половине листа формата A3 намечаем оси координат и из таблицы 1 согласно своему варианту берутся координаты точек А, В, С, D, Е, К, являющихся вершинами треугольников. Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями.
Задача на пересечение треугольников сводится к решению двух задач на пересечение прямой и плоскости. При решении каждой из задач находится одна точка пересечения прямой с плоскостью. Соединив две найденные точки, Вы получите линию пересечения треугольников.
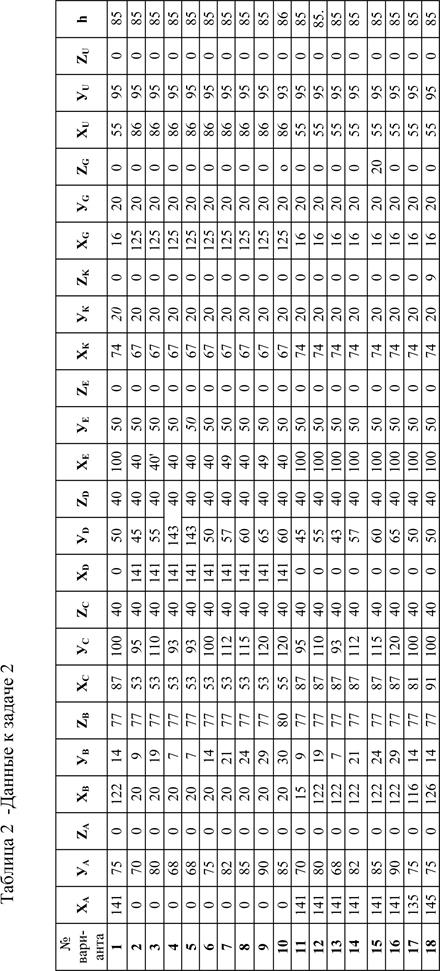
Таблица 1 – Данные к задаче 1
| № варианта | ХА | уа | za | Хв | Ув | zb | Хс | Ус | Zc | XD | УD | zd | ХЕ | уе | ze | Хк | ук | zk |
Алгоритм нахождения точки пересечения прямой с плоскостью треугольника - (DK) ∩ Δ АВС:
1. Заключаем (DK) во вспомогательную проецирующую плоскость α (α ^π2):
(D ״ K ״) ≡ f ״ оα
2. Находим линию (прямую) пересечения плоскости α сΔ АВС = (3 4):
f ״ оα ∩ Δ А ״ В ״ С ״⇒
f ״ оα ∩ (A ״ B ״) = 3 ״ → 3 ׳ Є (A ׳ B ׳)
f ״ оα ∩ (A ״ C ״) = 4 ״ → 4 ׳ Є (A ׳ C ׳)

3. Находим точку пересечения полученной линии (3 4) с прямой (DK):
(3 ׳ 4 ׳) ∩ (D ׳ K ׳) = M ׳ → M ״ Є (D ״ K ״)
4. m – одна из точек линии пересечения треугольников
Видимость сторон треугольников определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными жирными линиями, невидимые следует показать штриховыми линиями.
Все вспомогательные построения должны быть обязательно показаны на чертеже в виде тонких линий. Все буквенные или цифровые обозначения, а также надписи выполняются также в карандаше.
Задача 2. Определить натуральную величину треугольника ABC. В качестве исходного треугольника выбираем треугольник АВС из задачи № 1.
Натуральная величина треугольника ABC определяется методом плоскопараллельного перемещения. Для перемещения треугольника рекомендуем воспользоваться построением одной из главных линий плоскости (горизонталью или фронталью). Далее треугольник ABC перемещают на свободное поле, перенося точки методом триангуляции (треугольников), и затем вращением вокруг проецирующей прямой треугольник приводится в положение, когда он будет параллелен плоскости проекций. После всех построений получим натуральную величину треугольника.
Лист 2
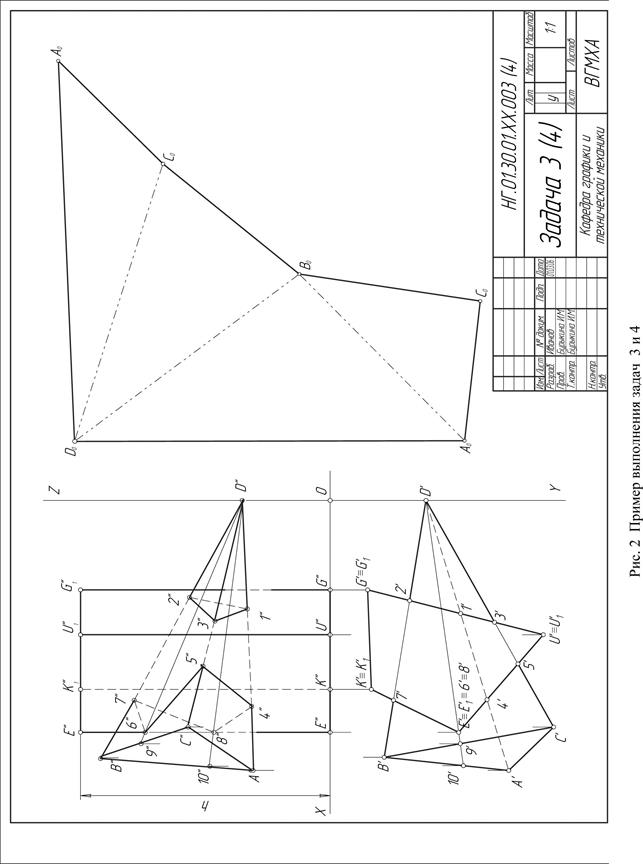
Задача 3. Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из таблицы 2. Пример выполнения листа 2 приведен на рисунке 2.
На листе намечаются оси координат и из таблицы 2 согласно своему варианту берутся координаты точек А, В, С, D, являющихся вершинами пирамиды, и координаты точек Е, К, G и U, являющимися вершинами многоугольника нижнею основания призмы, фронтальная проекция призмы достраивается на высоту h, данные которой приведены в таблице.
Призма своим основанием стоит на плоскости π1, поэтому горизонтальные проекции ее вертикальных ребер проецируются в точки вершин основания. Грани боковой поверхности призмы представляют собой отсеки горизонтально-проецирующих плоскостей.
Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника.
Например:
1. Находим точку пересечения ребра пирамиды (DA) c гранями призмы GG1UU1 и UU1EE1
(D ׳ A ׳) ∩ (G ׳ U ׳) = 1 ׳ → 1 ״ Є (G ״ U ״)
(D ׳ A ׳) ∩ (U ׳ E ׳) = 4 ׳ → 4 ״ Є (U ״ E ״)
Ребро пирамиды пересекает грань призмы в точках 1 и 4.
Особое внимание следует обратить на нахождения точек пересечения ребер призмы с гранями пирамиды:
 |
Например:
Ребро призмы (Е ׳ Е ׳ 1) пересекает грани пирамиды АDB и СDB
(Е ׳ Е ׳ 1) ∩ Δ А ׳ D ׳ B ׳ = 6 ׳ ⋀(Е ׳ Е ׳ 1) ∩ Δ С ׳ D ׳ B ׳ = 8 ׳ ⇒ 6 ׳ ≡8 ׳.
Для нахождения недостающих проекций точек 6 и 8 на гранях пирамиды необходимо провести вспомогательные прямые (образующие) на поверхности пирамиды.
Соединяя фронтальные проекции найденных точек, получаем линию (линии) пересечения многогранников. При построении линии пересечения следует учитывать правило:
- соединять можно только точки лежащие в одной плоскости (на одной грани),
- линия пересечения многогранников – замкнутая кривая линия.
Видимыми являются те отрезки линии пересечения, которые принадлежат видимым граням пирамиды или призмы. Их следует показать сплошными основными линиями. Невидимые отрезки пространственной ломаной показывать штриховыми линиями. Все вспомогательные построения на эпюре сохранить и показать их тонкими линиями.
Задаче следует уделить особое внимание. Все построения на чертеже тщательно проверить. Допущенные здесь ошибки приводят к неправильному решению следующей задачи (задача 4 - построение развертки пирамиды).
Задача 4. Построить развертку пирамиды. Пример выполнения задачи приведен на рисунке 2.
Развертка – плоская фигура, получаемая в результате совмещения поверхности с плоскостью. При этом все грани изображаются в натуральную величину, а потому прежде чем строить развертку необходимо определить натуральную величину всех ребер и сторон основания пирамиды.
Нахождение натуральной величины отрезка (длины ребра или стороны основания) можно проводить методом вращения или плоскопараллельного перемещения. Чтобы не загромождать чертеж заданные элементы пирамиды можно перевести на кальку или чистый лист, где провести все вспомогательные построения.
На кальке определяют натуральную величину каждого из ребер пирамиды и каждой из сторон основания. Зная натуральные величины этих отрезков, строят ее развертку.
Кальку или листы писчей бумаги прикрепить к листу 2.
Линии сгиба (ребра многогранника) на развертке показывают штриховой линией с двумя точками.
Лист 3
Задача 5 Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения представляют собой взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из таблицы 5.
Таблица 3 – Данные к задаче 5
| № варианта | ХK | уK | zK | R | h | Хe | Уe | Ze | r |
В правой половине листа намечаются оси координат, и из таблицы 5 берутся координаты точек и размеры, которыми задаются поверхности конуса и цилиндра. Определяют центр (точка К) окружности радиусом R основания конуса в горизонтальной плоскости π1. На фронтальную плоскость конус проецируется в виде треугольника высотой h до вершины конуса. Осью цилиндра вращения является фронтально-проецирующая прямая, проходящая через точку Е, основаниями цилиндра являются окружности радиусом r. Горизонтальная проекция цилиндра представляет собой прямоугольник, длиной Зr, обозначающей высоту цилиндра.
С помощью вспомогательных секущих плоскостей определяются точки пересечения одной поверхности с другой. Для построения линии пересечения конуса и цилиндра необходимо воспользоваться алгоритмом к решению задачи 5.
Чем больше взято вспомогательных точек, тем точнее кривизна линии пересечения. Точки, лежащие на крайних образующих конуса и цилиндра определяются с помощью линий связи.
По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.
Все основные вспомогательные построения на эпюре сохранить и показать тонкими сплошными линиями.
 |
Продолжение таблицы 4
В правой половине листа намечаются оси координат, и из таблицы 5 берутся координаты точек и размеры, которыми задаются поверхности конуса и цилиндра. Определяют центр (точка К) окружности радиусом R основания конуса в горизонтальной плоскости π1. На фронтальную плоскость конус проецируется в виде треугольника высотой h до вершины конуса. Осью цилиндра вращения является фронтально-проецирующая прямая, проходящая через точку Е, основаниями цилиндра являются окружности радиусом r. Горизонтальная проекция цилиндра представляет собой прямоугольник, длиной Зr, обозначающей высоту цилиндра.
С помощью вспомогательных секущих плоскостей определяются точки пересечения одной поверхности с другой. Для построения линии пересечения конуса и цилиндра необходимо воспользоваться алгоритмом к решению задачи 5.
Чем больше взято вспомогательных точек, тем точнее кривизна линии пересечения. Точки, лежащие на крайних образующих конуса и цилиндра определяются с помощью линий связи.
По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.
Все основные вспомогательные построения на эпюре сохранить и показать тонкими сплошными линиями.