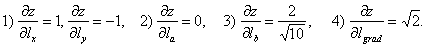Производная по направлению и градиент функции.
Что же такое производная по направлению? Производную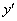 
функции одной переменной смело можно назвать производной по направлению – ведь она характеризует скорость изменения функции 
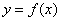в направлении оси 
.
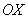И эта суть распространяется на производные функций нескольких переменных, в частности, на производные функции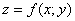 
. Геометрически функция двух переменных чаще всего представляет собой поверхность, и значения «зет» у нас чётко ассоциируются с высотой. Таким образом, с позиций геометрии скорость изменения данной функции – есть скорость изменения высоты. При этом совершенно понятно, что «негоризонтальная» поверхность изменчива – в каких-то направлениях она крутА, в каких-то полога, а где-то - «равнина». И производная по направлению как раз призвана охарактеризовать «ландшафт местности» (скорость изменения функции) в различных точках по различным направлениям. В этой связи возникает первый вопрос:
А КАКИМ СПОСОБОМ вообще можно задать какое-то конкретное направление?
Возьмем декартову систему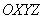 
, функцию 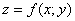. Давайте встанем в некоторую точку 
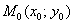области определения. В зависимости от выбора точки нам доступен бесконечно малый «шажок» в некоторых или, что вероятнее, во всех направлениях. Направление традиционно обозначается исходящим из точки 
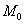лучом 
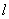, лежащим в плоскости 
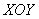. Сам луч можно определить с помощью угла (между ним и осью 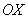либо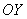 
), а ещё лучше – с помощью вектора.
Вопрос второй: как узнать скорость изменения функции 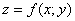в каком-либо направлении?
С помощью производной по направлению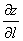 
. Как вариант, в обозначении можно использовать букву «эф»: 
.
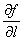Если в точке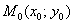 
существует производная по направлению луча 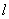(исходящего из точки 
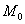и лежащего в плоскости 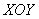), то её можно рассчитать по следующей формуле:
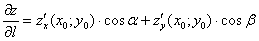, где:
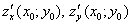– частные производные 1-го порядка в точке ; 
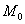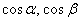– направляющие косинусы (координаты вектора единичной длины), однозначно определяющие данное направление.
На практике популярна более компактная запись: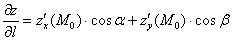 
.
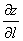– это ЧИСЛО, характеризующее скорость изменения функции, причём:
– если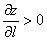 
, то функция 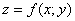в точке 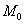по данному направлению возрастает (поверхность «идёт в гору»);
– если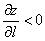 
, то функция 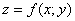в точке 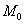по данному направлению убывает («склон» поверхности);
– если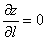 
, то функция 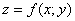в точке 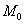по данному направлению постоянна (поверхность параллельна плоскости ).
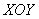Геометрический смысл производной по направлению.
Представьте плоскость, проходящую через луч «эль» перпендикулярно плоскости 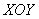. Данная плоскость «высекает» из поверхности 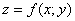пространственную линию 
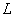, которой принадлежит точка 
.
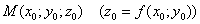Производная по направлению численно равна тангенсу угла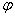 
между касательной к линии 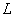в точке 
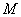и плоскостью : 
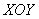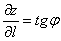
Также можно сказать, что 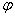-э то угол между касательной к линии 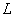в точке 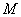и её ортогональной проекцией на плоскость 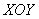, т.е. направлением луча 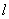( Более того, само обозначение 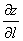символизирует отношение приращения функции («высоты») к бесконечно малому «шажку» по направлению луча «эль». Таким образом, чем 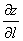больше по модулю, тем больше крутизна поверхности в данной точке по данному направлению. Крутизну можно выразить непосредственно через угол: 
.
Кстати, почему мы делаем именно бесконечно малые «шаги» по различным направлениям? Дело в том, что существует поверхности, «рельеф» некоторых меняется невероятно быстро – на 1 квадратном сантиметре могут запросто умещаться миллионы «гор» и «ущелий», да и того больше. Поэтому для корректного описания «местности» и используются бесконечно малые величины
Вернёмся к самой формуле 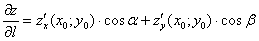, из которой выведем скорость изменения функции в двух хорошо знакомых направлениях.
Рассмотрим исходящий из точки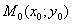 
луч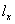 
, параллельный оси 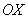(либо совпавший с ней) и направленный в сторону её острия. Данный луч однозначно определяется единичным вектором 
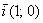. Таким образом, 
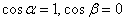(координаты вектора единичной длины – это и есть соответствующие направляющие косинусы) и общая формула упрощается: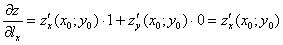 
То есть, частная производная «по икс» в точке 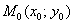характеризует скорость изменения функции 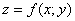в направлении острия оси 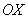(параллельно данной оси).
Для луча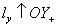 
– 
.
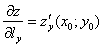Пример 1 Найти производную функции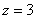 
в точке 
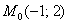по направлению вектора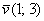 
Решение: Вычислим скорость изменения функции 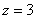по направлению исходящего из точки 
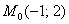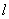луча , который определяется вектором 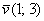. Используем рабочую формулу: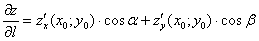
Найдём частные производные 1-го порядка: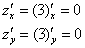 
В результате получены две константы, а именно, два нуля. Что это значит? Это значит, что частные производные равны нулю В ЛЮБОЙ точке области определения функции 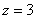(вся плоскость 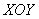), в частности и в точке : 
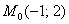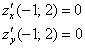
Формально частные производные можно расписать в виде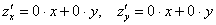 
и выполнить подстановку координат точки : 
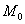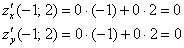
Полученные результаты подтверждают тот факт, что откуда бы и по какому бы направлению мы ни передвигались – наша высота 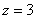будет сохраняться постоянной:
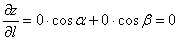
Найдём направляющие косинусы предложенного направления. По существу, требуется найти вектор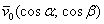 
единичной длины, который сонаправлен с вектором .
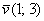Напоминаю: координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси).
Направляющие косинусы ненулевого вектора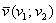 
, заданного в ортонормированном базисе 
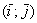, выражаются формулами 
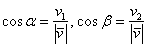, а сами координаты вектора можно выразить через его длину и данные косинусы: 
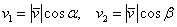, то есть: 
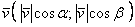. Причём, для любого ненулевого вектора справедливо равенство 
.
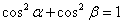Кроме того, вектор с координатами из соответствующих направляющих косинусов:
– коллинеарен исходному вектору «вэ»;
– его длина равна единице (так называемый единичный вектор).
Воспользуемся готовой формулой: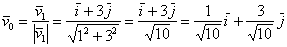 
Любой другой ненулевой сонаправленный вектор приводится к этому же «эталону». Протестируем, например, вектор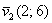 
:
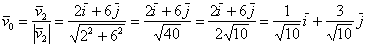
Убедимся, что его длина действительно равна единице:
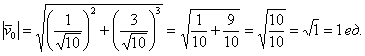
Способ проверки основан на известном равенстве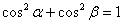 
:
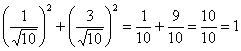
В итоге получаем: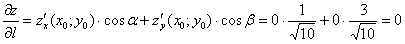 
Ответ: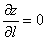
Проведённые выкладки справедливы и для любой другой «горизонтальной» плоскости, то есть производная функции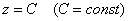
в любой точке и по любому направлению равна нулю.
Пример 2 Найти производную функции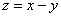 
в точке 
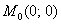по направлению:
1) координатных осей (параллельно им);
2) вектора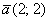 
;
3) вектора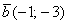 
;
4) градиента.
Решение: итак, возьмем произвольную точку «зелёного холма». Теперь переместимся в какую-нибудь другую точку плоскости :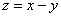
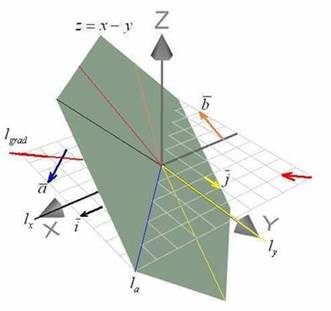
Во всех своих точках плоскость имеет постоянный наклон по всем направлениям, то есть, с точки зрения наклона – без разницы, где мы находимся. Проверим это аналитически: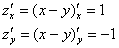 
Как и в предыдущем примере, производные-константы подразумевают тот факт, что в ЛЮБОЙ точке плоскости XOY, а значит и в точке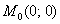 
эти значения сохраняются постоянными: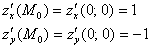 
Таким образом: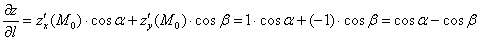 
– и данный результат как раз подтверждает то, что скорость изменения функции 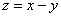зависит только от направления.
1) Найдём производную по направлению луча 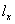, совпадающего с положительной полуосью 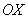. Тут даже с направляющими косинусами возиться не надо – как было установлено выше, производная по данному направлению равна частной производной по «икс» в точке : 
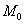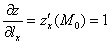Аналогичная история с положительным направлением 
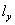оси :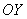 
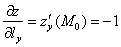
Отрицательный знак производной говорит об убывании функции 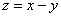в направлении координатного вектора 
.
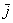2) Вычислим производную по направлению луча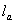 
. Для этого отработанным приёмом найдём единичный вектор 
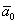, сонаправленный с вектором :
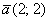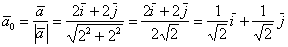– координаты которого и являются направляющими косинусами данного направления: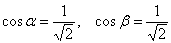 
Проверка: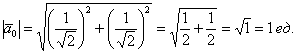 
,
Запишем вычисления подробно:
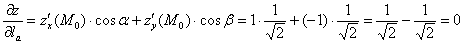
И действительно, синяя «дорожка» проходит на неизменной высоте прямо в плоскости .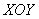
Аналогично – если мы «выйдем» из любой другой точки плоскости 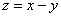по направлению того же вектора 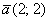, то наша высота (скорость изменения функции) будет оставаться постоянной.
3) Найдём производную по направлению вектора :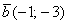
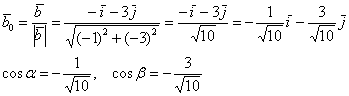Проверим результат с помощью равенства : 
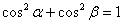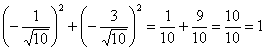
Вычислим производную по направлению луча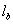 
, который «спрятался» под плоскостью :
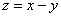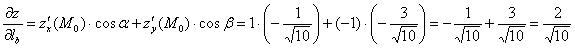
4) Градиент функции в точке 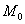– это вектор, указывающий направление наибыстрейшего роста данной функции в точке 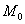. Если совсем просто, то куда «смотрит» градиент – там и самый крутой «подъём в гору»
Распространённые обозначения: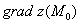 
либо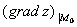 
,
Определение: Градиентом функции 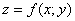в точке 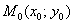называется направленный отрезок 
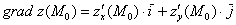, отложенный от точки 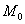, который показывает направление наискорейшего возрастания функции 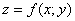в данной точке.
В нашем примере: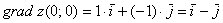 
.
Взаимосвязь производной по направлению с градиентом:
Производная по некоторому направлению 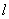в точке 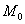– это проекция градиента в данной точке на данное направление: 
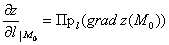, откуда, получается весьма полезная практическая формула: 
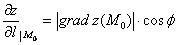, где: 
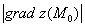– длина градиента; 
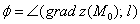– угол между градиентом и данным направлением.
В свою очередь из этой формулы следует, что производная по направлению достигает максимального значения при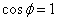 
, то есть когда 
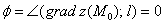– направление 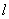совпадает с направлением градиента. В нашей задаче производная по направлению градиента: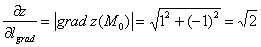 
Ответ: 