Определители и матрицы, решение систем
Задача1.1 Вычислить определитель третьего порядка 
а) по правилу треугольника;
б) с помощью разложения по элементам какой-либо строки или столбца.
Решение.
а) Вычислим данный определитель по правилу треугольника:

 .
.
б) Вычислим данный определитель с помощью разложения по элементам третьего столбца:


Задача 1.2 Для матриц  найти: а)
найти: а)  ,
,
б)  , в)
, в) 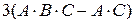 , г)
, г) 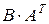 , д)
, д)  .
.
Решение:
а)

б)


в) 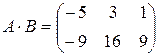



г) 

д)

Найдем для матрицы В обратную.
 , значит
, значит  существует.
существует.
Найдем алгебраические дополнения для элементов матрицы  .
.


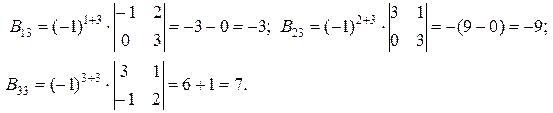
Тогда 
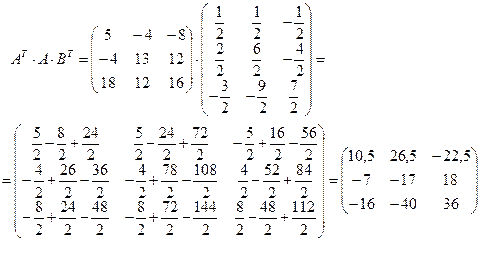
Ответ: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 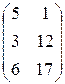 ; д)
; д)  .
.
Задача 1.3 Дана система трех линейных уравнений с тремя неизвестными 
Требуется:
а) найти её решения с помощью формул Крамера;
б) записать систему в матричном виде и решить её средствами матричного исчисления;
в) решить систему методом Гаусса.
Решение: 1) Рассмотрим матрицу системы линейных уравнений  .
.
Главный определитель матрицы d = 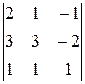 = 2 ×3 × 1 + 1 × (–2) × 1 + 1× 3 ×
= 2 ×3 × 1 + 1 × (–2) × 1 + 1× 3 ×
∙ (–1) – (–1) × 3 × 1 – 1× (–2) × 2 –1× 3 ×1 = 5 (вычислили по правилу треугольника).
Так как d = 5 ¹ 0, то система имеет единственное решение, которое и можно найти по формулам Крамера. Для системы трех уравнений с тремя неизвестными формулы Крамера имеют вид:  где d 1, d 2 и d 3 – получаются из определителя d заменой соответственно первого, второго и третьего столбца на столбец из свободных членов. Составим и вычислим эти определители, используя, например, правило треугольника.
где d 1, d 2 и d 3 – получаются из определителя d заменой соответственно первого, второго и третьего столбца на столбец из свободных членов. Составим и вычислим эти определители, используя, например, правило треугольника.
 ,
,
 ,
,
 .
.
По формулам Крамера получаем:  ,
,  ,
,  .
.
2) Данную систему можно представить в матричном виде: А×Х=В, где  – матрица системы уравнений,
– матрица системы уравнений,  – матрица-столбец из неизвестных,
– матрица-столбец из неизвестных,  – матрица-столбец из свободных членов.
– матрица-столбец из свободных членов.
Умножим слева обе части уравнения на А –1, где А –1 – обратная для матрицы А матрица. Тогда 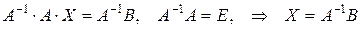 . Значит, решение матричного уравнения А×Х=В будем искать в виде Х=А –1 × В, где А –1 – матрица, обратная матрице А.
. Значит, решение матричного уравнения А×Х=В будем искать в виде Х=А –1 × В, где А –1 – матрица, обратная матрице А.
Так как определитель матрицы А не равен нулю (d= 5), то обратная матрица существует и равна:  , где
, где  – алгебраическое дополнение для элементов исходной матрицы.
– алгебраическое дополнение для элементов исходной матрицы.
Найдем алгебраические дополнения для элементов матрицы А:
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;  .
.
Получаем  . Тогда
. Тогда
 .
.
3) Решим систему методом Гаусса, для это расширенную матрицу системы с помощью элементарных преобразований приведем ступенчатому виду:  . Для удобства поменяем местами первую и последнюю строки.
. Для удобства поменяем местами первую и последнюю строки.
 |
 ~
~  - поменяем местами вторую и третью строки, получим:
- поменяем местами вторую и третью строки, получим:  .
.
Этой матрице соответствует система  .
.
Из последнего уравнения находим  . Подставляя данное значение во второе уравнение, находим
. Подставляя данное значение во второе уравнение, находим  . Подставляя найденные значения в первое уравнение, находим
. Подставляя найденные значения в первое уравнение, находим 
Ответ: х = 3; y = 1; z = 2.
Аналитическая геометрия
Задача 2.1 Коллинеарны ли векторы 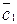 и
и  , построенные по векторам
, построенные по векторам  и
и 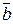
, если  .
.
Решение: Найдём координаты векторов 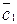 и
и  :
:

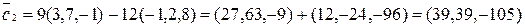 .
.
Найдём отношения соответствующих координат векторов  и
и  :
:
 .
.
Так как координаты пропорциональны, то 
 .
.
Ответ: 
 .
.
Задача 2.2 Найти скалярное произведение векторов  , если
, если

Решение:
воспользуемся определение скалярного произведения векторов  и свойствами скалярного произведения:
и свойствами скалярного произведения:
 =
=

б) Воспользуемся геометрическим смыслом модуля векторного произведения:
 .
.
Найдём векторное произведения векторов  , выраженных через вектора
, выраженных через вектора  , используя свойства векторного произведения:
, используя свойства векторного произведения:
Найти площадь параллелограмма построенного на векторах  , если
, если 
 .
.

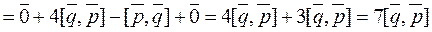 ,
,
тогда 
Ответ: а) 30, б) S = 84 кв. ед.
Ответ: S = 84 кв. ед.
Задача 2.3 Дан треугольник  с вершинами
с вершинами  . Найти:
. Найти:
а) величину угла 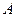 ;
;
б) координаты точки пересечения медиан;
в) координаты точки пересечения высот;
г) длину высоты, опущенной из вершины 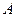 ;
;
д) площадь треугольника  ;
;
е) уравнение прямой, проходящей через вершину  параллельно стороне
параллельно стороне  ;
;
ж)систему неравенств, задающих область внутри треугольника.
Решение: Найдем уравнения сторон треугольника  и угловые коэффициенты, используя уравнение прямой, заданной двумя точками:
и угловые коэффициенты, используя уравнение прямой, заданной двумя точками:
 .
.
Уравнение прямой 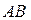 :
:  , отсюда
, отсюда  или
или  . Угловой коэффициент прямой
. Угловой коэффициент прямой  равен
равен  .
.
Уравнение прямой  :
:  , отсюда
, отсюда 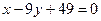 или
или  . Угловой коэффициент прямой
. Угловой коэффициент прямой  равен
равен 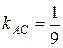 .
.
Уравнение прямой  :
:  , отсюда
, отсюда  или
или  .
.
Угловой коэффициент прямой  равен
равен  .
.
а) вычислим внутреннюю величину угла  треугольника
треугольника  :
:
 , отсюда (по таблице Брадиса или с помощью инженерного калькулятора),
, отсюда (по таблице Брадиса или с помощью инженерного калькулятора),  радиан.
радиан.
б) Обозначим:  - точку пересечения медиан,
- точку пересечения медиан,  и
и 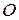 - середины отрезков
- середины отрезков  и
и  соответственно.
соответственно.
Найдем координаты середин сторон, используя формулы  , и уравнения соответствующих медиан.
, и уравнения соответствующих медиан.
Точка  :
:  ,
,
тогда уравнение медианы 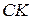 :
:  , отсюда
, отсюда  .
.
Точка О:  ,
,
тогда уравнение медианы 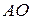 :
: 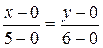 , отсюда
, отсюда  .
.
Координаты точки пересечения медиан найдем, решая систему уравнений, задающих медианы:
 , т.е
, т.е  .
.

Рисунок Треугольник  с вершинами
с вершинами  .
.
в) Обозначим через  - точку пересечения высот
- точку пересечения высот  и
и  .
.
Уравнение высоты  будем искать в виде:
будем искать в виде:  .
.
Так как прямые  и
и  перпендикулярны, то
перпендикулярны, то  . Тогда
. Тогда  или
или 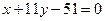 .
.
Уравнение высоты  будем искать в виде
будем искать в виде  .
.
Так как прямые  и
и  перпендикулярны, то
перпендикулярны, то  .
.
Тогда  или
или  .
.
Координаты точки пересечения высот найдем, решая систему уравнений, задающих высоты:
 , т.е
, т.е  .
.
г) длину высоты  найдем по формуле расстояния от точки до прямой:
найдем по формуле расстояния от точки до прямой:  .
.
У нас это точка  и прямая
и прямая 
 :
:  (ед.).
(ед.).
д) площадь треугольника найдем по формуле:  .
.
Получаем  (кв.ед.).
(кв.ед.).
е) так как искомая прямая параллельна стороне 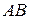 , то их угловые коэффициенты равны. Используя уравнение
, то их угловые коэффициенты равны. Используя уравнение  , получаем:
, получаем:  или
или  .
.
ж) Каждая прямая делит плоскость на две полуплоскости. Уравнение прямой  :
:  ; уравнение прямой
; уравнение прямой  :
:  ; уравнение прямой
; уравнение прямой  :
:  .
.
Для определения нужной полуплоскости берем любую точку, лежащую внутри треугольника, например точку (1,1), и подставляем ее координаты в уравнения прямых.
Получаем:  ,
,  ,
,  .
.
Следовательно, система неравенств имеет вид:  .
.
Ответ: а) 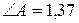 радиан; б)
радиан; б)  ; в)
; в)  ; г)
; г)  (ед.);
(ед.);
д)  (кв.ед.); е)
(кв.ед.); е)  ; ж)
; ж)  .
.
Задача 2.4 Составить канонические уравнения:
а) эллипса, большая полуось которого равна 3, а фокус находится в точке  ;
;
б) гиперболы с мнимой полуосью равной 2, и фокусом  ;
;
в) параболы, имеющей директрису 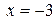 .
.
Решение:
а) Каноническое уравнение эллипса имеет вид  .
.
По условию задачи  ,
,  . Для эллипса справедливо равенство
. Для эллипса справедливо равенство 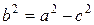 .
.
Для нашей задачи получаем:  .
.
Подставляя в каноническое уравнение эллипса, поучаем: 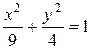 .
.
б) Каноническое уравнение гиперболы имеет вид 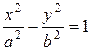 .
.
По условию задачи  ,
, 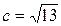 . Для гиперболы справедливо равенство
. Для гиперболы справедливо равенство  .
.
Для нашей задачи получаем:  .
.
Подставляя в каноническое уравнение гиперболы, поучаем:  .
.
в) Каноническое уравнение параболы в нашем случае имеет вид  , а уравнение ее директрисы
, а уравнение ее директрисы  .
.
По условию задачи уравнение директрисы 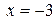 . Поэтому
. Поэтому 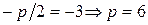 .
.
Подставляя в каноническое уравнение параболы, поучаем  .
.
Ответ: а)  ; б)
; б)  ; в)
; в)  .
.
Задача 2.5 По координатам вершин А (3; – 2; 2), В (1; – 3; 1), С (2; 0; 4),
D (6; – 4; 6) пирамиды АВСD найти:
а) длины ребер АВ и АС;
б) угол между векторами  ;
;
в) объем пирамиды АВСD;
г) высоту, опущенную из вершины D на грань АВС;
д) уравнение прямой АВ;
е) уравнение плоскости ВСD;
ж) синус угла между прямой АВ и плоскостью ВСD;
з) косинус угла между плоскостью xOy и плоскостью ВСD.
Решение: Найдем координаты векторов  ,
,  ,
,  :
:



а) Длины ребер АВ и АС найдем как длины векторов  и
и  :
:
 ,
,  ,
,
т.е.  (ед.),
(ед.), 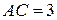 (ед.).
(ед.).
б) Угол между векторами  и
и  найдём, используя скалярное произведение векторов:
найдём, используя скалярное произведение векторов:  тогда
тогда



в) Объём пирамиды равен  объёма параллелепипеда, построенного на векторах
объёма параллелепипеда, построенного на векторах 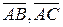 и
и  , как на сторонах. Объём параллелепипеда найдём, используя смешанное произведение векторов:
, как на сторонах. Объём параллелепипеда найдём, используя смешанное произведение векторов:
 .
.
Объём параллелепипеда равен  (ед3). Тогда объём пирамиды равен
(ед3). Тогда объём пирамиды равен  (ед3).
(ед3).
г) Из школьного курса известна формула объёма пирамиды:  . Отсюда
. Отсюда  .
.
Площадь основания найдём, используя векторные произведения векторов:
 , то есть вектор векторного произведения имеет координаты (0, 5, -5).
, то есть вектор векторного произведения имеет координаты (0, 5, -5).
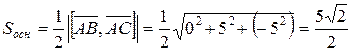 (ед.2).
(ед.2).
 (ед.).
(ед.).
д) Для нахождения уравнения прямой АВ используем уравнение прямой, проходящей через две заданные точки:  . Имеем:
. Имеем: 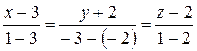 ,
,
 – каноническое уравнение искомой прямой.
– каноническое уравнение искомой прямой.
 – общее уравнение искомой прямой.
– общее уравнение искомой прямой.
е) Для нахождения уравнения плоскости ВСD используем уравнение плоскости, проходящей через три заданные точки:  .
.
Имеем: 
т.е. 
 – искомое уравнение, или
– искомое уравнение, или 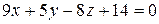 .
.
ж) синус угла между прямой АВ и плоскостью ВСD (это угол между направляющим вектором прямой и нормальным вектором плоскости) находится по формуле:
 .
.
Получаем:
 .
.
з) косинус угла между плоскостью xOy и плоскостью ВСD найдем по формуле:
 .
.
Получаем
 .
.
Ответ: а)  ; б)
; б)  ; в) 5; г)
; в) 5; г)  ; д)
; д)  ;
;
е) 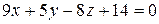 ; ж)
; ж)  ; з)
; з)  .
.
Ведение в математический анализ
Задача 3.1 Вычислить пределы функции: а) – в)  , при
, при 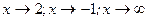 ,;
,;
г)  ; д)
; д)  .
.
Решение. а)  .
.
б)  .
.
Разложим числитель и знаменатель на множители:

Получаем: 
в)  .
.
г) 
д)  . Воспользовались тем, что при
. Воспользовались тем, что при  .
.
Ответ: а)  , б) -1/2, в) 0, г) 0, д)
, б) -1/2, в) 0, г) 0, д) 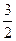 , е)
, е)  .
.
Задача 3.2 Исследовать функцию на непрерывность, определить характер точек разрыва. Изобразить график функции в окрестностях точек разрыва.
а) 
б)  .
.
Решение:
а) Знаменатель обращается в ноль при х = 0 и х = 2. найдем односторонние пределы в этих точках:
 ,
,
 .
.
Так как односторонние пределы конечные, но не равные между собой, то в точке х = 0 функция имеет разрыв первого рода неустранимый.
 ,
,  .
.
Так как получили бесконечные пределы, то в точке х = 2.разрыв второго рода.
Рассмотрим поведение функции на бесконечности:
 ,
,  .
.
б) На каждом из промежутков соответствующая функция является непрерывной. Вычислим односторонние пределы на границах промежутков:


В точке х = -1 функция непрерывна, так как односторонние пределы в этой точке равны между собой и равны значению функции в точке. В точке х = 1 - разрыв 1 – го рода, неустранимый, так как односторонние пределы конечные, но не равные между собой.
 у
у
-4 -1 0 1 х