Численные методы решения нелинейных уравнений
Определить корни уравнения графически и уточнить один из них итерационными методами.
, 
.
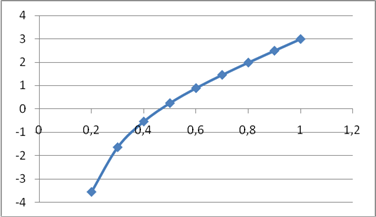
График функции на отрезке [0.2, 1]. Как видно из графика, решение около 0,45.
Метод деления отрезка пополам
Исходные данные:
| a | b | e | x | f(x) |
| 0,2 | 0,01 | 0,46875 | 0,023893 |
Программа:
PublicFunction F(x)
F = (x + 1) ^ 2 - 1 / x
EndFunction
PublicSubPopolam()
a = Cells(2, 1)
b = Cells(2, 2)
e = Cells(2, 3)
1 x = (a + b) / 2
If F(a) * F(x) < 0 Then b = x Else a = x
If (b - a) >= e Then GoTo 1
Cells(2, 4) = x
Cells(2, 5) = F(x)
EndSub
Метод Ньютона (метод касательных)
Проверяем выполнение условия сходимости на концах заданного интервала: 
- выполняется. За начальное приближение корня можно принять 
.
Исходные данные:
| x0 | e | x | F(x) |
| 0,2 | 0,01 | 0,46557 | -1,02E-05 |
Программа:
Public Function F(x)
F = (x + 1) ^ 2 - 1 / x
End Function
Public Function F1(x)
F1 = 2 * (x + 1) + 1 / x / x
End Function
Public Sub Nyton()
x = Cells(2, 1)
e = Cells(2, 2)
1 xk = x - F(x) / F1(x)
If Abs(xk - x) >= e Then x = xk: GoTo 1
Cells(2, 3) = xk
Cells(2, 4) = F(xk)
EndSub
Метод простой итерации
Определяем значение M:
Исходные данные:
| x0 | e | M | x | F(x) |
| 0,001 | 0,465699 | 0,000963 |
Программа:
Function F(x)
F = (x + 1) ^ 2 - 1 / x
End Function
Sub Iter()
x = Cells(2, 1)
e = Cells(2, 2)
M = Cells(2, 3)
1 xk = x - F(x) / M
If Abs(xk - x) >= e Then x = xk: GoTo 1
Cells(2, 4) = xk
Cells(2, 5) = F(xk)
End Sub
Решение СЛАУ (систем линейных алгебраических уравнений)
Решить систему уравнений методом Гаусса:
Решение приведено в другом документе (в приложении).
Решение СЛАУ (систем линейных алгебраических уравнений)
Решить систему уравнений методом прогонки (или итерационным методом с точностью 0,01)
Метод прогонки
Исходные данные:
| a | b | c | d | x | r |
| 1,344086 | -8,9E-16 | ||||
| -1 | 0,967742 | -4,4E-16 | |||
| -1 | 2,215054 | 1,78E-15 | |||
| 1,892473 |
Программа:
Public Sub Progonka()
Const n = 4
Dim a(n), b(n), c(n), d(n), u(n), v(n), x(n + 1), r(n)
For i = 1 To n
a(i) = Cells(i + 1, 1)
b(i) = Cells(i + 1, 2)
c(i) = Cells(i + 1, 3)
d(i) = Cells(i + 1, 4)
u(i) = -c(i) / (a(i) * u(i - 1) + b(i))
v(i) = (d(i) - a(i) * v(i - 1)) / (a(i) * u(i - 1) + b(i))
Next i
For i = n To 1 Step -1
x(i) = u(i) * x(i + 1) + v(i)
Next i
For i = 1 To n
r(i) = d(i) - a(i) * x(i - 1) - b(i) * x(i) - c(i) * x(i + 1)
Cells(i + 1, 5) = x(i)
Cells(i + 1, 6) = r(i)
Next i
EndSub
Решить систему уравнений итерационным методом с точностью 0,01
Метод Якоби
| x1 | x2 | x3 | x4 |
| 1,666667 | 0,75 | 2,4 | |
| 1,416667 | 0,933333 | 1,95 | 1,8 |
| 1,355556 | 0,883333 | 2,226667 | 2,025 |
| 1,372222 | 0,967778 | 2,171667 | 1,886667 |
| 1,344074 | 0,949861 | 2,216222 | 1,914167 |
| 1,350046 | 0,968037 | 2,207139 | 1,891889 |
| 1,343988 | 0,964273 | 2,21523 | 1,896431 |
| 1,345242 | 0,96781 | 2,213569 | 1,892385 |
| 1,344063 | 0,967082 | 2,215085 | 1,893216 |
Программа
Public Sub Prog2()
Dim X1(10), X2(10), X3(10), X4(10)
X1(1) = Cells(2, 1)
X2(1) = Cells(2, 2)
X3(1) = Cells(2, 3)
X4(1) = Cells(2, 4)
For i = 2 To 10
X1(i) = (5 - X2(i - 1)) / 3: Cells(i + 1, 1) = X1(i)
X2(i) = (3 - X1(i - 1) + X3(i - 1)) / 4: Cells(i + 1, 2) = X2(i)
X3(i) = (12 + X2(i - 1) - X4(i - 1)) / 5: Cells(i + 1, 3) = X3(i)
X4(i) = (6 - X3(i - 1)) / 2: Cells(i + 1, 4) = X4(i)
Next i
End Sub
МетодЗейделя
| x1 | x2 | x3 | x4 |
| 1,666667 | 0,333333 | 2,466667 | 1,766667 |
| 1,555556 | 0,977778 | 2,242222 | 1,878889 |
| 1,340741 | 0,97537 | 2,219296 | 1,890352 |
| 1,341543 | 0,969438 | 2,215817 | 1,892091 |
| 1,343521 | 0,968074 | 2,215197 | 1,892402 |
| 1,343975 | 0,967805 | 2,215081 | 1,89246 |
| 1,344065 | 0,967754 | 2,215059 | 1,892471 |
| 1,344082 | 0,967744 | 2,215055 | 1,892473 |
| 1,344085 | 0,967742 | 2,215054 | 1,892473 |
Программа
Public Sub Prog3()
Dim X1(10), X2(10), X3(10), X4(10)
X1(1) = Cells(2, 1)
X2(1) = Cells(2, 2)
X3(1) = Cells(2, 3)
X4(1) = Cells(2, 4)
For i = 2 To 10
X1(i) = (5 - X2(i - 1)) / 3: Cells(i + 1, 1) = X1(i)
X2(i) = (3 - X1(i - 1) + X3(i - 1)) / 4: Cells(i + 1, 2) = X2(i)
X3(i) = (12 + X2(i - 1) - X4(i - 1)) / 5: Cells(i + 1, 3) = X3(i)
X4(i) = (6 - X3(i - 1)) / 2: Cells(i + 1, 4) = X4(i)
Next i
EndSub
Численное интегрирование
Вычислить интеграл 
по квадратурным формулам прямоугольников, трапеций, парабол. n=6.
Вычисляем интеграл по формулам средних прямоугольников, трапеций, парабол.
| a | |
| b | |
| n | |
| h | 0,5 |
| Ср. прям | 39,23419 |
| Трапеций | 53,68516 |
| Симпсона | 52,63814 |
Программа
Public Function F(x)
F = 7 * x ^ 2 - 3 * Sqr(x)
End Function
Public Sub Integr()
a = Cells(1, 2)
b = Cells(2, 2)
n = Cells(4, 2)
s1 = 0: s2 = 0: s3 = 0
h = (b - a) / n
Cells(5, 2) = h
x = a
Do While x < b
s1 = s1 + F(x) * h
x = x + h
Loop
Cells(6, 2) = s1
s2 = (F(a) + F(b)) / 2
x = a + h
Do While x < b
s2 = s2 + F(x)
x = x + h
Loop
s2 = s2 * h
Cells(7, 2) = s2
h = (b - a) / 2 / n
s3 = 0
x = a
Do While x < b
s3 = s3 + h * (F(x) + 4 * F(x + h) + F(x + 2 * h)) / 3
x = x + 2 * h
Loop
Cells(8, 2) = s3
End Sub
Решение Задачи Коши для дифференциального уравнения первого порядка.
Решить задачу Коши методами Эйлера, модифицированным методом и методом Рунге-Кутты на заданном отрезке:
.
Программы
Public Function f(x, y)
f = y - 2 * x * x + 3
End Function
Public Sub Prog1() // МетодЭйлера
k = 0
x = 0
h = 0.2
y = 4
Do While x <= 1
y = y + h * f(x, y)
Cells(2 + k, 1) = k
Cells(2 + k, 2) = x
Cells(2 + k, 3) = y
k = k + 1
x = x + h
Loop
End Sub
PublicSubprog2() // Модифицированный метод Эйлера
k = 0
x = 0
h = 0.2
y = 4
Do While x <= 1
y1 = y + h * f(x, y)
y = y + h * (f(x, y) + f(x + h, y1)) / 2
Cells(2 + k, 5) = x
Cells(2 + k, 6) = y
k = k + 1
x = x + h
Loop
End Sub
Public Sub prog3() //МетодРунге-Кутта
k = 0
x = 0
h = 0.2
y = 4
Do While x <= 1
k0 = h * f(x, y)
k1 = h * f(x + h / 2, y + k0 / 2)
k2 = h * f(x + h / 2, y + k1 / 2)
k3 = h * f(x + h, y + k2)
y = y + (k0 + 2 * k1 + 2 * k2 + k3) / 6
Cells(2 + k, 8) = x
Cells(2 + k, 9) = y
k = k + 1
x = x + h
Loop
EndSub
Результат работы программы:
| k | x | y | x | y | x | y | ||
| 5,4 | 5,532 | 5,544187 | ||||||
| 0,2 | 7,064 | 0,2 | 7,36744 | 0,2 | 7,395424 | |||
| 0,4 | 9,0128 | 0,4 | 9,537877 | 0,4 | 9,58627 | |||
| 0,6 | 11,27136 | 0,6 | 12,08181 | 0,6 | 12,15649 | |||
| 0,8 | 13,86963 | 0,8 | 15,04621 | 0,8 | 15,15465 | |||
| 16,84356 | 18,48837 | 18,64008 |
Приближение функции по методу наименьших квадратов (МНК)