Решение транспортной задачи

IIПрактическая часть

Решение финансовых задач в MSExcel

Задача 1

Требуется рассчитать 9-летнею ипотечную ссуду со ставкой 7% годовых при начальном взносе 20% суммы и ежемесячной (ежегодной) выплате.

 

Решение задачи

Для решения данной задачи использовались следующие функции.

ПЛТ(ставка;кпер;пс;бс;тип)

Ставка — процентная ставка по ссуде.

Кпер — общее число выплат по ссуде.

Пс — приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.

Бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0.

Тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.

Исходные данные для решения задачи приведены на рис.2.1

Рис.2.1 Исходные данные

Формулы для решения задачи приведены на рис.2.2

Рис.2.2 Решения задачи.

Результаты решения приведены на рис.2.3

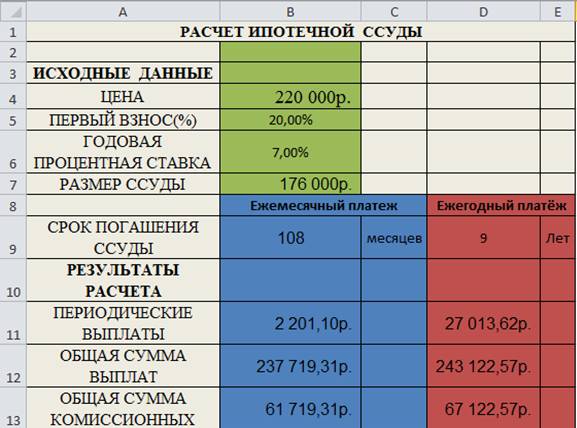
Рис.2.3Результаты решения

 

Вывод.

При расчёте 9-летней ипотечной ссуды со ставкой 7% годовых при начальном взносе 20% суммы и ежемесячной (ежегодной) выплате. Общая сумма выплат составит 237713,31.

Задача 2.

Рассмотреть возможность инвестиций 22000 руб. Возврат 5000 руб. через год, 8000 руб. через два года и т. д. 5000 руб. — через 5 лет.

 

Рис.2.4Исходные данные

Решение задачи

ЧПС – Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).

Рис.2.5Решения задачи.

Рис.2.6 Результаты решения

Вывод.

При расчёте инвестиций на 5 лет, с возвратом по 5000,8000,8000,7000,8000 рублей с процентной ставкой более 15% имеет смысл.

Задача 3.

Рассмотреть возможность инвестиций 220000 руб. Возврат по 33000 руб. в течение 9 лет. При какой годовой процентной ставке это имеет смысл?

Рис.2.7 Исходные данные

Решение задачи

ПС(ставка; кпер; выплата; бз; тип)

ставка — процентная ставка за период;

кпер — общее число периодов выплат;

выплата — величина постоянных периодических платежей;

бз — будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр бз опущен, то его значение по­лагается равным о (будущая стоимость займа, например, равна о);

тип — число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если же его значение равно 1, то в начале периода.

Рис.2.8 Решения задачи.

 

Рис.2.9 Результаты решения.

Вывод

При рассмотрении возможности инвестиций 220000 руб на 9 лет. С ежегодным возвращением по 33000 руб. С процентной ставкой более 15%, есть выгода.

Задача 4.

Вычислить основные платежи, плату по процентам, общую ежегодную выплату и остаток долга на примере ссуды 220000 руб. под годовую ставку7% на срок 9 лет.

Рис.2.10 Исходные данные

 

Решение задачи

Присвойте ячейкам следующие имена:

Ячейка Имя

B1 Процент

B2 Срок

B3 Ежегодная_плата

B4 Размер_ссуды

Кроме того, в ячейки введите формулы:

Ячейка Формула Описание

ВЗ =ПЛТ(Процент;Срок;–Размер_ссуды) Ежегодная плата

D6 =Размер_ссуды Начальный остаток долга

А7 =A6+1 Номер года

В7 =D6*Процент Плата по процентам

С7 =Ежегодная_плата-В7 Основная плата за первый год

D7 =ЕСЛИ(D6-С7<>0;D6-С7) Остаток долга за первый год

Рис.2.11 Решения задачи

Рис.2.12 Результаты решения.

Вывод.

Были вычислены основные платежи, плата по процентам, общая ежегодная выплата.

Задача 5.

Рассмотреть возможность инвестиций 220000 руб. под годовую ставку 5%. Возможна выплата по 33000 руб. в год. Сколько лет займут эти выплаты?

 

Рис.2.13Исходные данные

Решение задачи

КПЕР (ставка; выплата; нз; бз; тип)

ставка — процентная ставка за период;

выплата — величина постоянных периодических платежей;

нз — текущее значение, т. е. общая сумма, которую составят будущие платежи;

бз — будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр бз опущен, то его значение по­лагается равным 0 (будущая стоимость займа, например, равна 0);

тип— число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если его значение равно 1, то в начале периода.

Рис.2.14Решения задачи.

 

Рис.2.15Результаты решения

Вывод.

При расмотрении инвестиций на сумма 220000 руб. под годовую ставу 5% и возможных выплат по 33000 руб. Выплаты зайдут 6 лет.

Задача 6.

Рассмотреть возможность инвестиций 22000 руб. С выплатами в определенные дниИмеет ли смысл это при годовой ставке 15 % (Сумма выплат из задания 2).

Рис.2.16Исходные данные

Решение задачи

ЧПС (ставка; 1-е значение; 2-е значение;...)

ставка — процентная ставка за период;

1-е значение, 2-е значение,... — от 1 до 29 аргументов, представляющих расходы и доходы. 1-е значение, 2-е значение,... должны быть равно­мерно распределены по времени и осуществляться в конце каждого пе­риода. НПЗ использует порядок аргументов 1-е значение, 2-е значение,…для определения порядка поступлений и платежей.

 

Рис.2.17Решения задачи.

Рис.2.18Результаты решения

Вывод.

Рассмотрев возможность инвестиций 22000 руб. С выплатами в определенные дни Имеет смысл это при годовой ставке 15 %.

Задача 7.

Составить отчетную ведомость реализации товаров 5 магазинами с Июля по Октябрь,

 

 

Рис.2.19Исходные данные

 

Решение задачи.

В этой отчетной ведомости надо определить:

суммарную и среднюю выручку каждого из магазинов за отчетный период;

суммарную выручку всех магазинов за каждый месяц отчетного периода;

место, которое занимает каждый из магазинов в суммарном объеме вы­ручки;

долю каждого из магазинов в суммарном объеме выручки;

количество магазинов, имеющих суммарную выручку до 1000 млн руб., от 1000 млн руб. до 1500 млн руб., от 1500 млн руб. до 2000 млн руб. и свы­ше 2000 млн руб.

 

Рис.2.20Решения задачи.

Рис.2.21Результаты решения

Вывод.

Составлена отчетная ведомость реализации товаров 5 магазинами с Июля по Октябрь,

 

 

Задача 8.

Рассмотреть возможность инвестиций 3100 руб. под годовую ставку 4% и собираетесь отдавать по 500 руб. в год. Сколько лет займут выплаты?

Рис.2.22Исходные данные

Решение задачи.

КПЕР (ставка; выплата; нз; бз; тип)

ставка — процентная ставка за период;

выплата — величина постоянных периодических платежей;

нз — текущее значение, т. е. общая сумма, которую составят будущие платежи;

бз — будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если параметр бз опущен, то его значение по­лагается равным 0 (будущая стоимость займа, например, равна 0);

тип— число, равное 0 или 1, обозначающее, когда должна производиться выплата. Если значение параметра тип равно 0 или он опущен, то оплата производится в конце периода, если его значение равно 1, то в начале периода.

 

Рис.2.23Решения задачи.

 

Вывод.

Рассмотрели возможность инвестиций 3100 руб. под годовую ставку 4 % с выплатами по 500 руб. выплаты займут 7 лет

Задача 9.

Рассмотреть возможность вкладывать по 178 руб. в течение 12 лет при годовой ставке 4%. Сколько денег будет на счету через 12лет?

Рис.2.24Исходные данные

Решение задачи.

БС(ставка;кпер;плт;пс;тип)

Ставка — это процентная ставка за период.

Кпер — это общее число периодов платежей по аннуитету.

Плт — это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно плт состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если аргумент опущен, должно быть указано значение аргумента пс.

Пс — это приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент нз опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плт.

Тип — это число 0 или 1, обозначающее, когда должна производиться выплата. Если этот аргумент опущен, то он полагается равным 0.

 

Рис.2.25Решения задачи.

Вывод.

При рассмотрении возможности вкладывать по 178 руб. в течение 12 лет при годовой ставке 4%. Денег будет через 12 лет 1670,54 руб.

Задача 10.

Определить процентную ставку для 7 летнего займа в 3100 руб. с ежегодной выплатой в 500руб.

 

Рис.2.26Исходные данные

Решение задачи.

СТАВКА(кпер;плт;пс;бс;тип;предположение)

Кпер — общее число периодов платежей по аннуитету.

Плт — регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента бс

Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.

Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бзс для займа равно 0).

Тип — число 0 или 1, обозначающее, когда должна производиться выплата.

Рис.2.27Решения задачи.

Вывод.

Определена процентная ставку для 7 летнего займа в 3100 руб. с ежегодной выплатой в 500руб.

Задача 11.

Составить таблицу начисления премии по итогам работы сети n магази­нов с июля по ноябрь по следующему правилу:

если продукции продано не меньше чем на 65000 руб., то комиссионные составляют 3%;

за первое место дополнительно начисляется 5%, за второе место – 2,5%,за третье место – 1,25%.

 

Рис.2.28Исходные данные

Решение задачи

Ср. значение находит среднее арифметическое значение из указанного диапазона ячеек.

Синтаксис:

СРЗНАЧ (число1; число2; …)

Функция ранг возвращает ранг числа в списке чисел. Ранг числа - это его величина относительно других значений в списке. (Если список от­сортировать, то ранг числа будет его позицией.)

Синтаксис:

РАНГ(число; ссылка; порядок)

число — число, для которого определяется ранг;

ссылка — массив или ссылка на список чисел. Нечисловые значения в ссылке игнорируются;

порядок — число, определяющее способ упорядочения. Если значение параметра порядок равно 0 или он опущен, то MS Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в поряд­ке убывания. Если значение параметра порядок является любым ненуле­вым числом, то MS Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке возрастания.

Функция ранг присваивает одинаковым числам одинаковый ранг.

Функция частота возвращает распределение частот в виде вертикального массива. Для данного множества значений и данного множества карманов (т.е. интервалов в математическом смысле) частотное распределе­ние подсчитывает, сколько исходных значений попадает в каждый интервал.

Синтаксис:

ЧАСТОТА (массив_данных; двоичный__массив)

массив_данных — массив или ссылка на множество данных, для которых вычисляются частоты; если массив_данных не содержит значений, то функция частота возвращает массив нулей;

двоичный_массив — массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. ЕСЛИ двоичный_массив не содержит значений, то функция частота возвращает количество эле­ментов в аргументе двоичный_массив.

 

 

Рис.2.29Решения задачи.

Вывод.

Задача 12.

Предприятие владеет основными средствами 65000 руб. Рассчитать показатели амортизации за 5лет.

Рис.2.30Исходные данные

Решение задачи

АПЛ Возвращает величину амортизации актива за один период, рассчитанную линейным методом.

АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации)

Нач_стоимость — затраты на приобретение актива.

Ост_стоимость — стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества).

Время_эксплуатации — количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации).

 

 

Рис.2.31Решения задачи.

Рис.2.32Результаты решения

Вывод.

Предприятие владеет основными средствами 65000 руб. Рассчитали показатели амортизации за 5лет.Результат амортизации 11744,84 руб.

Задача 13.

Предприятие владеет основными средствами. Рассчитать показатели амортизации за период при следующих условиях. Дополнительные условия: Амортизация за первый год.

 

Рис.2.33Исходные данные

Решение задачи

ДДОБ (стоимость; остаточная_стоимость; время__эксплуатации; период;коэффициент)

стоимость — начальная стоимость имущества;

остаточная_стоимость — остаточная стоимость в конце периода;

время__эксплуатации — количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);

время_эксплуатации — количество периодов, за которые амортизируется имущество (иногда называется временем полной амортизации);

период — номер периода для вычисления амортизации (должен быть из­мерен в тех же единицах, что и время полной амортизации);

коэффициент — норма снижения балансовой стоимости (амортизации).Если коэффициент опущен, то предполагается, что он равен 2 (метод двукратного учета амортизации).

 

Рис.2.34Решения задачи.

Рис.2.35Результаты решения

 

Вывод.

Предприятие владеет основными средствами 65000руб. Рассчитать показатели амортизации за период 5лет. при дополнительном условии: вычислении амортизации за первый год равной 26000руб.

Решение транспортной задачи

Имеются n пунктов производства и k пунктов рас­пределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения cij приведена в таблице, где под строкой понимается пункт производства, а под столбцом — пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирую­щий суммарные транспортные расходы.

 

Исходные данные:

Рис.3.1 Исходные данные

 

Решение задачи:

Для решения данной задачи построим ее математическую модель. Неизвест­ными здесь являются объемы перевозок. Пусть xij — объем перевозок с i-й фабрики в j-й центр распределения. Функцией цели являются суммарные транспортные расходы, т. е.

где Сij — стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения. Кроме того, неизвестные должны удовлетворять следующим ограничениям:

неотрицательность объема перевозок;

т. к. модель сбалансирована, то вся продукция должна быть вывезена с фабрик, и потребность всех центров распределения должна быть пол­ностью удовлетворена.

Таким образом, мы имеем следующую модель:

минимизировать:

при ограничениях:

где аi — объем производства на i-й фабрике, bj — спрос в j-м центре распределения.

 

Рис.3.2 формулы

 

Рис.3.3 Результаты

Заключение

В главе было дано понятие комплексной системы управления предприятием и ее роль и задачи в управлении предприятием. Также были рассмотрены основные задачи, которые должны быть решены на предприятии при внедрении КИС, подходы к созданию КИС и способы решения основные проблем, возникающих при внедрении.

 

Размещено на Allbest.ru