СИЛА УПРУГОСТИ И ВЕС ТЕЛА

ЛИСТ 11 9 КЛАСС

Деформацией тела называется изменение его размеров или формы. Растяжение и сжатие, сдвиг, изгиб и кручение — все это различные виды деформаций.

Сила, действующая со стороны деформированного тела на соприкасающиеся с ним тела и направленная в сторону, противоположную перемещению частей тела при его деформации, называется силой упругости.

Тела, которые полностью восстанавливают свою форму или объем после прекращения действия сил, вызывающих деформации, называются упругими телами. Но наряду с упругими телами (резиновый шнур, стальной шарик и др.) имеются тела пластичные, которые после прекращения действия внешних сил, вызвавших деформацию, не восстанавливают своей формы (мокрая глина, свинцовый шарик).

Зависимость силы упругости от деформации установил экспериментально современник Ньютона английский ученый Роберт Гук. Открытый Гуком закон справедлив только для упругой деформации, т. е. для тех случаев, когда после пре­кращения действия сил, деформирующих тело, оно возвраща­ется в исходное состояние (восстанавливаются форма и раз­меры тела).

Таким образом, при упругой деформации растяжения (или сжатия) модуль силы упругости прямо пропорционален модулю изменения длины тела. В этом и состоит закон Гука.

Записывается закон Гука так:

,

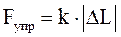где ÷DL÷ - модуль изменения длины тела.

Коэффициент пропорциональности k называют коэф­фициентом упругости или жёсткостью тела. В системе СИ жесткость выражается в ньютонах на метр (Н/м). Жёсткость зависит от материала, из которого изготовлено тело, от его размеров и формы.

Учитывая, что координата х конца деформированного тела, которая для недеформированного тела равна нулю, и проекция силы упру­гости на ось Х имеют противоположные знаки, можно записать:

.

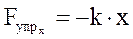Сила, с которой тело вследствие его притяжения Землей действует на опору или растягивает подвес, называется весом тела.

Пусть тело находится в кабине лифта, движущегося с ускорением а.

Согласно второму закону Ньютона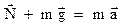

По третьему закону Ньютона вес тела , поэтому получим:

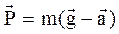
Вес тела в лифте, движущемся с ускорением, направленным вертикально вверх, больше веса покоящегося тела. Увеличение веса тела, вызванное ускоренным движением опоры (или подвеса), называется перегрузкой. Перегрузку можно оценить, взяв отношение веса ускоренно движущегося тела к весу покоящегося тела:

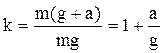
Вопросы к зачёту: Деформация. Упругость. Сила упругости. Закон Гука. Коэффициент жёсткости. Вес. Вес тела, движущегося с ускорением. Невесомость.

1. Два тела с массами 1 кг и 2 кг соединены невесомой пружиной, жёсткость которой 200Н/м. Тела находятся на абсолютно гладкой горизонтальной поверхности. Ко второму телу приложена горизонтальная сила 20Н. Определите удлинение пружины.

2. Имеются две пружины, жёсткости которых равны соответственно к₁ и к₂. Какова жёсткость двух пружин, соединённых: а) параллельно, б) последовательно?

3. Вертикально расположенная пружина соединяет два груза. Масса верхнего груза 2 кг, а нижнего 3 кг. Когда система подвешена за верхний груз, длина пружины равна 10 см. Если же систему поставить на подставку, длина пружины оказывается равна 4 см. Определите длину ненапряжённой пружины.

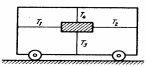4. Четырьмя натянутыми нитями груз закреплён на тележке. Силы натяжения горизонтальных нитей равны соответственно Т₁ и Т₂, а вертикальных - Т₃ и Т₄.

С каким ускорением тележка движется по горизонтальной плоскости?

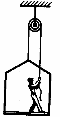5. Маляр работает в подвесной люльке. Ему понадобилось срочно подняться вверх. Он принимается тянуть верёвку с такой силой, что его давление на пол люльки уменьшилось до 400Н. Масса люльки 12 кг, масса маляра 72 кг. Каково ускорение люльки? Чему равна сила натяжения троса, на котором подвешен лёгкий блок?

6. Какая сила действует в поперечном сечении однородного стержня длины L на расстоянии х от конца, к которому вдоль стержня приложена сила F?

7.(6.19) Веревка длиной L = 12 м и массой m = 6 кг пере­кинута через невесомый блок. Какова сила натяжения ве­ревки в ее середине в тот момент, когда длина веревки по одну сторону от блока равна l = 8 м?

8. (Г.2.29) Тело А движется по горизонтальному столу под действием силы натяжения привязанной к нему нити. Нить перекинута через прикреплённый к столу невесомый блок и привязана к другому телу В, падающему вниз. 1) Определить натяжение нити, если масса тела А равна 200 г, масса тела В – 300 г, коэффициент трения 0,25. 2) Как изменится ответ, если тела поменять местами?

9.(6.11) Два тела массами m₁ и m₂ соеди­нены пружиной и подвешены на нити к потолку (рис. 6.8). Нить перерезают. С ка­кими ускорениями начнут двигаться тела?

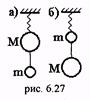10.(6.47) Два шара с массами М и m со­единены нитью и подвешены к пружине как показано на рис. 6.27. Если перере­зать нить в случае а), то шар М придет в движение с ускорением а₁. Каково бу­дет ускорение шара m, если перерезать нить в случае б)?

11. Из тонкого резинового жгута массы m и жёсткости k сделали кольцо радиуса R₀. Это кольцо раскрутили вокруг его оси. Найдите новый радиус кольца, если угловая скорость его вращения равна w.При какой угловой скорости длина кольца увеличится вдвое? При какой угловой скорости кольцо обязательно разорвется? Считать, что закон Гука выполняется вплоть до момента разрыва кольца.

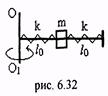
12.(6.55) Муфта массой m насажена на гладкий горизонтальный стержень длиной 2L₀ и скреплена двумя одинаковыми пружинами с осью ОO₁ и упором на конце стержня (рис. 6.32). В отсутствие вращения пружины ненагружены, а их жестко­сти равны K. Систему раскручивают вокруг оси ОО₁. Найти зависимость расстояния от оси до муфты от угловой скоро­сти вращения. Размерами муфты пренебречь.

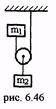
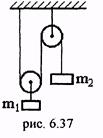13.(6.65) Определить ускорения грузов и силу натяжения нити в системе из подвижного и неподвижного блоков (рис. 6.37). Нить и блоки идеальны, массы гру­зов равны m₁ и m₂.

14.(6.80)Найти ускорения брусков в системе (рис. 6.46)

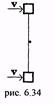15.(6.60)Два тела массой m, связанные нитью длиной L, движутся со скоростью V, направлен­ной перпендикулярно нити, по горизонтально­му гладкому столу. Середина нити натыкается на вбитый в стол гвоздь (рис. 6.34). Какова си­ла натяжения нити сразу после этого?

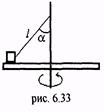16.(6.58) На горизонтальном диске лежит небольшой брусок, привя­занный нитью длиной L к оси дис­ка. Нить натянута и составляет с вертикалью угол α (рис.(6.33)) Диск начинают медленно раскру­чивать. При какой угловой скорости вращения диска брусок оторвется от него? Какова при этом будет сила натяжения нити? Масса бруска равна m.

17.(6.41) Два тела, связанные нитью, движутся вниз с уско­рением вдвое большим ускорения свободного падения. Во сколько раз сила натяжения нити, за которую тянут тела больше силы натяжения нити, связывающей тела? Масса нижнего тела в три раза больше массы верхнего.