Задача 1
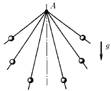
Из точки А по спицам с разным наклоном одновременно начинают скользить без трения маленькие бусинки. На какой кривой будут находиться бусинки в момент времени t?
Задача 2
Свободно падающее тело пролетело мимо точки А со скоростью vА. С какой скоростью оно пролетит мимо точки В, находящейся на h ниже точки А?
Задача 3
По гладкой наклонной плоскости со скоростью v пускают шарик. Какое расстояние по горизонтали он пройдет, прежде чем скатится с плоскости? Плоскость наклонена к горизонту под углом 45°. Начальная скорость шарика образует угол 45° с горизонтальным краем плоскости.
Задача 4
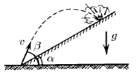Из подствольного гранатомета ведут стрельбу по укрытиям расположенным на склоне горы. На каком расстоянии от стрелка будут падать гранаты, если их начальная скорость v, угол наклона горы α и угол стрельбы по отношению к горизонту β?
Задача 5
Утка летела по горизонтальной прямой с постоянной скоростью u. Неопытный охотник бросил в нее камень, причем бросок был сделан без упреждения, то есть в момент броска скорость камня v была направлена на утку под углом α к горизонту. На какой высоте летела утка, если камень все-таки попал в нее?
Задача 6
В трубу длины L, наклоненную под углом α к горизонту, влетает шарик с горизонтальной скоростью v. Определите время пребывания шарика в трубе, если удары шарика о ее стенки упругие.
Задача 7
Какую минимальную скорость должен иметь камень, брошенный человеком, чтобы он перелетел дом высоты H и длины L, если бросок совершается с высоты h и для броска человек может выбрать любое место?
Задача 8
С какой скоростью должен лететь спутник вокруг Земли, чтобы, все время «падая» с ускорением g, двигаться по круговой орбите? Высота полета спутника 600 км над уровнем моря, радиус Земли 6400 км, а ускорение свободного падения на высоте 600 км равно 8,2 м/с2.
|
|
Задача 9
Самолеты летят по одной прямой навстречу друг другу с одинаковой скоростью v. Предельная дальность обнаружения ими друг друга l. Один самолет после обнаружения другого совершает разворот, не меняя модуля скорости, и летит параллельно второму самолету. При каком постоянном ускорении разворачивающегося самолета самолеты потеряют друг друга из вида в конце разворота?
Задача 10
Сферический резервуар, стоящий на земле, имеет радиус R. При какой наименьшей скорости брошенный с земли камень может перелететь через резервуар, лишь коснувшись его вершины?
Задача 11
Снаряд вылетает из пушки со скоростью v под углом α к горизонту. Какое время снаряд приближается к пушке?
Преобразование Галилея.
Задача 1
Одна из звезд нашей вселенной покоится, а все остальные звезды разлетаются от нее в разные стороны со скоростями, пропорциональными расстояниям от них до покоящейся звезды. Какую картину движения обнаружит наблюдатель, движущийся вместе с другой звездой нашей вселенной?
Задача 2
Какой будет продолжительность полета из Новосибирска в Москву и обратно, если полет проходит по прямой, а в течение всего времени полета дует ветер со скоростью u под углом α к трассе? Скорость самолета относительно воздуха v, длина трассы L. При каком направлении ветра продолжительность полета максимальна?
Задача 3
Тело налетает на стенку со скоростью v под углом α к линии, перпендикулярной стенке. Определите скорость тела после упругого удара, если стенка: а) неподвижна; б) движется перпендикулярно самой себе со скоростью w навстречу телу; в) движется под углом β к линии, перпендикулярной ей самой, со скоростью w навстречу телу.
|
|
Задача 4
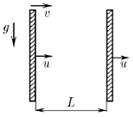
Тело влетает горизонтально со скоростью v в пространство между двумя вертикальными стенками, которые перемещаются со скоростью u. Определите скорость тела после n -го удара о переднюю стенку. Расстояние между стенками L. Удары абсолютно упругие. Ускорение свободного падения g.
Задача 5
Между двумя стенками со скоростью v летает шарик. Одна из стенок начинает с бесконечно-малой скоростью приближаться к другой. Начальное расстояние между стенками L. Какой будет скорость шарика, когда расстояние между стенками будет L/2? Столкновения шарика со стенками упругие.
Задача 6
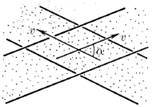Два пучка частиц, движущихся с одинаковой по модулю скоростью v, пересекаются под углом α. Соударения частиц происходят в ограниченной области. Перейдем к системе отсчета, в которой скорости частиц равны по модулю и противоположны по направлению. Казалось бы, теперь область пересечения – весь объем пучков, и поэтому число соударений в единицу времени должно быть больше. Объясните получившееся противоречие.
Задача 7
Мальчик, который может плавать со скоростью, в два раза меньшей скорости течения реки, хочет переплыть эту реку так, чтобы его как можно меньше снесло вниз по течению. Под каким углом к берегу он должен плыть? На какое расстояние его снесет, если ширина реки равна 200 м?
Движение со связями.
|
|
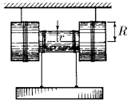
Задача 1
Угловая скорость катушки равна ω, радиус внутреннего цилиндра r, а радиус внешних цилиндров R. Каковы скорости оси катушки и груза относительно земли?
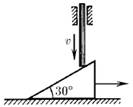
Задача 2
На клине с углом α лежит монета. С каким наименьшим ускорением должен двигаться клин по горизонтальной плоскости, чтобы монета свободно падала вниз?
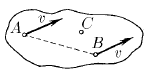
Задача 3
Скорости точек A и B твердого тела равны v. Скорость точки С, находящейся в плоскости прямой AB и вектора v, равна u > v. Найдите проекцию скорости точки С на ось, перпендикулярную указанной плоскости.
Задача 4
Постройте траектории точек колеса, катящегося без проскальзывания по рельсу. Рассмотрите случаи когда точки находятся от оси колеса на расстоянии: r > R, r = R, r < R. Найдите ускорение этих точек, если ось колеса движется с постоянной скоростью v. Найдите радиус кривизны траектории точки, находящейся в высшем и низшем положениях на расстоянии r ≠ R от оси колеса.
Задача 5
Луна обращена к Земле постоянно одной стороной. Сколько оборотов совершит она вокруг своей оси за время полного оборота вокруг Земли?
Задача 6
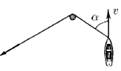Веревку, привязанную к лодке, тянут за свободный конец таким образом, чтобы она не провисала. Лодка движется с постоянной скоростью v, образуя в некоторый момент времени угол α с отрезком веревки, находящимся между столбом и лодкой. С какой скоростью нужно тянуть в этот момент времени свободный конец веревки?
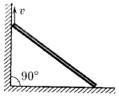
Задача 7
Стержень длины L упирается своими концами в стороны прямого угла. Верхний конец стержня поднимают со скоростью v. Найдите, как зависит от времени скорость его нижнего конца. Начало отсчета времени считать моментом, когда верхний конец стержня находится в вершине прямого угла.
Задача 8
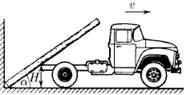Бревно, упираясь нижним своим концом в угол между стеной и землей, касается дна грузовика на высоте H от земли. Найдите угловую скорость бревна в зависимости от угла α между ним и горизонтом, если грузовик отъезжает от стены со скоростью v.