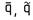ПРИМЕРЫ СИМВОЛИЧЕСКОЙ ЗАПИСИ

ЗАДАЧИ

ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

 

Методические указания

к практическим занятиям студентов

по дисциплине

«Начертательная геометрия, инженерная и

компьютерная графика»

для студентов дневной и заочной

форм обучения по специальностям:

7.080401 Информационные управляющие системы и технологии;

7.090701 Радиотехника;

7.090801 Микроэлектроника и полупроводниковые приборы;

7.090804 Физическая и биомедицинская электроника;

7.091401 Системы управления и автоматики;

7.091501 Компьютерные системы и сети;

7.100301 Судовождение;

7.100302 Эксплуатация судовых энергетических установок.

8.092201 Электрические системы и комплексы транспортных средств

 

Севастополь

 

УДК 515(075)

 

Задачи по начертательной геометрии: Методические указания к практическим занятиям по дисциплине «Начертательная геометрия, инженерная и компьютерная графика» для студентов дневной и заочной форм обучения. / Разраб. А.Ф. Медведь, В.Г. Середа. – Севастополь: Изд-во СевНТУ, 2007. – 36 с.

 

Методические указания содержат условия задач с примерами составления алгоритмов их решения. Удачный подбор задач способствует развитию пространственного воображения студентов и приобретению навыков решения конструктивных задач.

 

Методические указания предназначены для студентов дневной и заочной форм обучения.

 

Методические указания утверждены на заседании кафедры начертательной геометрии и графики, протокол №11 от 21 июня 2007 г.

 

 

Допущено научно-методическим центром университета в качестве методических указаний.

 

Рецензент:

Смагин В.В., канд. техн. наук, доцент

 

 

СОДЕРЖАНИЕ

Введение……………………………………………………………….
1.	Обозначения и символы…………………...…………………….
2.	Примеры символической записи………………...………………
3.	Определения и понятия………………………………………….
4.	Свойства проецирования……………………………..…………
5.	Методические рекомендации…………………………………….
6.	Примеры решения задач….……………………………………..
7.	Задачи для решения………….………………….………….........
	Заключение
	Библиографический список

ВВедение

С целью повышения эффективности обучения студентов произведен отбор ключевых задач по темам курса.

Рекомендуемые задачи по темам лекций и расчетно-графических заданий приведены в таблице 1.

Таблица 1 – Рекомендуемая последовательность решения задач.

Темы занятий	Задачи для решения
В аудитории	Самостоятельно
Моделирование структуры геометрического объекта	1, 2, 5…8; 13, 14, 18…20; 27, 28	3, 4, 9…12; 15, 16, 21…26; 29…32
Моделирование метрических характеристик объектов	33…36;41, 43	37…40; 42, 44
Моделирование геометрических тел	45, 46, 49…52	47, 48, 53,56
Моделирование сечений геометрических тел	57, 60, 61	57, 58, 62
Моделирование линии пересечения поверхностей	60, 62
Моделирование разверток поверхностей

Отобранный минимум задач рекомендуется для аудиторной и самостоятельной работы студентов при подготовке к сдаче расчетно-графических работ, зачетов или экзаменов.

Обозначения и символы

Точка в пространстве обозначается прописными буквами латинского алфавита: A, B, C, D,…или цифрами: 1, 2, 3,…

Прямые и кривые линии – строчными буквами латинского алфавита: a, b, c, d,… Линии уровня – строчными буквами: горизонтали – h, фронтали – f, профильные – p.

– направляющие линии (соответственно прямые и кривые) поверхности; – образующие линии (соответственно прямые и кривые) поверхности.

Плоскости и поверхности – прописными буквами греческого алфавита: Σ, Δ, Ρ, Γ,…

Плоские углы – малыми буквами греческого алфавита: α, β, δ, η,…

Принятая система координат OXYZ.

Оси проекций на чертеже X₁₂, Y₁₃, Z₂₃, начало координат O.

Плоскости проекций – буквой Π с индексами 1, 2, 3, 4, 5,… Основные плоскости проекций: Π₁ – горизонтальная, Π₂ – фронтальная, Π₃ – профильная.

Проекции точек, прямых линий, плоскостей, поверхностей, углов – теми же буквами что и в пространстве, с добавлением подстрочного индекса соответствующей плоскости проекций: A₁, a₁, Σ₂, Δ₂ …

Центры и направления проецирования – S, U.

При замене плоскостей проекций новая ось – буквой с соот-ветствующим индексом: X₁₄, Y₂₅ и т.д.

Новое положение точки после одного вращения (перемещения) или после двух соответственно.

Плоскость аксонометрических проекций обозначается буквой Π со знаком штрих – Π'.

Аксонометрические проекции точек, прямых, плоскостей и углов обозначаются теми же буквами со штрихом – A', a', Σ',…

Вторичные проекции имеют внизу индекс прямоугольных проекций, а вверху – штрих: A₁', a₁', Σ₁'.

Аксонометрические оси обозначаются буквами X', Y', Z', начало координат буквой O.

Принятые символы:

º – тождественность; – скрещивание;

Ì – лежит на; – касание;

É – проходит через; Ù – и;

çç – параллельность; Ú – или;

^ – перпендикулярность; = – равно, есть;

Ç – пересечение; Þ – если…, то;

È – соединение;? – построить, определить;

/ – не;! – строим, определяем.

ПРИМЕРЫСИМВОЛИЧЕСКОЙ ЗАПИСИ

a || b Þ a₁ || b₁ – если прямые параллельны, то одноименные проекции этих прямых параллельны.

f ^ n Þ f₂ ^ n₂ Ù f₁ || x₁₂ – если прямые перпендикулярны (одна – линия уровня, а другая – общего положения), то одна пара их одноименных проекций перпендикулярна.

a Ç b Þ a_i Ç b_i = K_i Ù K₁K₂ ^ x₁₂ – если прямые пересекаются, то одноименные проекции прямых пересекаются в точках, лежащих на одной линии связи, перпендикулярной оси проекций.

? a É A Ù || b – построить прямую, проходящую через точку и параллельную другой прямой.

! a₁ É A₁ Ù || b₁ – строим горизонтальную проекцию прямой, проходящую через горизонтальную проекцию точки, и параллельную горизонтальной проекции другой прямой.

! 1= b Ç AC – строим точку как результат пересечения двух прямых.

! C₁ Ì A₁В₁ – строим горизонтальную проекцию точки на одноименной проекции прямой.

! D Ë D – строим точку, не лежащую на плоскости.

! n ^ D – строим прямую перпендикулярную заданной плоскости.

! h Ì D – строим горизонталь, лежащую на заданной плоскости.

! A Ì a – строим точку, лежащую на заданной прямой.

 

ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ

Аксонометрия– измерение по осям (осеизмерение).

Горизонтальная прямая плоскости – прямая, лежащая на плоскости и параллельная горизонтальной плоскости проекций

Инвариантность– неизменяемость.

Инцидентность – отношение принадлежности между парой геометрических элементов имеющих различную размерность. Инцидентность определяется понятиями "лежит на" и "проходит через".

Комплексный чертеж (эпюр Монжа) – графическая модель объекта, состоящая из связанных между собой ортогональных проекций, лежащих в одной плоскости.

Конкурирующие прямые – прямые, лежащие в плоскости частного положения.

Конкурирующие точки – точки, лежащие на одном проецирующем луче.

Координаты – числа, выражающие расстояние точки от трех плоскостей проекций.

Линейные объекты – прямая, плоскость, многогранник.

Линия наибольшего наклона к горизонтальной плоскости проекций – прямая, лежащая на плоскости и перпендикулярная горизонтальной прямой плоскости.

Линия наибольшего наклона к профильной плоскости проекций – прямая, лежащая на плоскости и перпендикулярная профильной прямой плоскости.

Линия наибольшего наклона к фронтальной плоскости проекций– прямая, лежащая на плоскости и перпендикулярная фронтальной прямой плоскости.

Линия связи – прямая, соединяющая две проекции точки.

Моделирование структуры объекта – построение проекций объекта.

Модель объекта – совокупность элементов, отображающих структуру объекта.

Наглядность чертежа – возможность установить по изображению форму объекта.

Нелинейные объекты– кривые линии и поверхности.

Обратимость чертежа – возможность определения истинных размеров изображенного объекта.

Объект – пространственная фигура, состоящая из геометрических элементов (точек, прямых, плоскостей).

Одноименные проекции – проекции элементов на одну и ту же плоскость проекций.

Ось проекций – линия пересечения двух плоскостей проекций.

Параллельность – отсутствие общих точек у двух прямых, лежащих в одной плоскости, или у прямой и плоскости или у двух плоскостей.

Пересечение – наличие общих точек у геометрических элементов.

Перпендикулярность – свойство двух прямых, прямой и плоскости или двух плоскостей, которые пересекаются друг с другом и образуют в точке пересечения прямой угол (две плоскости в этом случае образуют по линии пересечения двугранный прямой угол).

Плоскости проекций – три грани куба (горизонтальная, фронтальная и профильная плоскости проекций).

Плоскость параллелизма – плоскость, параллельная двум скрещивающимся прямым.

Поверхность– множество положений движущейся линии в пространстве.

Проекции многогранника – проекции его каркаса (с обозначением всех вершин).

Проекция – изображение объекта на плоскости (поверхности).

Развертка многогранника – это совмещение всех граней многогранника с одной плоскостью путем последовательного вращения их вокруг ребер.

Проецирование – процесс получения изображения (проекции) объекта или конструктивная связь между объектом и моделью.

Проецирующий луч – прямая, связывающая точку объекта с её проекцией.

Сечение многогранника – плоский многоугольник, число вершин которого равно числу пересеченных плоскостью ребер.

След прямой– точка пересечения прямой с плоскостью проекций.

След плоскости– линия (прямая) пересечения плоскости с плоскостью проекций.

Структура объекта – схема взаимного расположения элементов объекта.

Фронтальная прямая плоскости – прямая, лежащая на плоскости и параллельна фронтальной плоскости проекций.

Чертеж – графическая модель существующих или воображаемых (проектируемых) объектов.

Элементы геометрического объекта – точки, линии (прямые и кривые), поверхности (плоскости).

Свойства проецирования

Решение задач основано на знании свойств ортогонального проецирования, представленных в таблице 2.

Таблица 2 – Свойства ортогонального проецирования

1. Проекцией точки является точка.

2. Проекцией прямой является прямая (в общем случае).

 

Продолжение таблицы 2

3. Проекцией проецирующей прямой является точка - след прямой (проекция прямой вырождается в точку).	4. Проекция точки, лежащей на прямой, лежит на проекции этой прямой.
5. Проекцией проецирующей плоскости является прямая – след плоскости (проекция плоскости вырождается в прямую).	6. Проекция точки, принадлежащая проецирующей плоскости, лежит на следе плоскости.

 

Продолжение таблицы 2

7. Проекция прямой, принадлежащей проецирующей плоскости, совпадает со следом плоскости.	8. Проекции параллельных прямых параллельны.
9. Следы параллельных проецирующих плоскостей параллельны.	10. Следы проецирующей плоскости и проекция параллельной ей прямой параллельны.

 

Продолжение таблицы 2

11. Следы взаимно перпендикулярных проецирующих плоскостей перпендикулярны друг к другу.	12. След проецирующей плоскости и проекция перпендикулярной к ней прямой взаимно перпендикулярны.
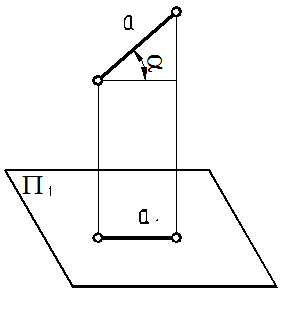
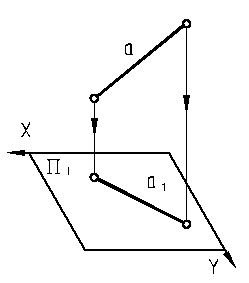
13. Проекции отрезка прямой, не параллельного плоскости проекций, меньше самого отрезка прямой, так как a1 = a cosa.	14. Проекция отрезка, параллельного плоскости проекций, равна самому отрезку (отрезок проецируется в истинную величину).

Продолжение таблицы 2

15. Проекции двух взаимно перпендикулярных пересекающихся или скрещивающихся прямых, одна из которых параллельна плоскости проекций, взаимно перпендикулярны.	16. Следы двух проецирующих плоскостей образуют угол, равный углу между этими плоскостями.
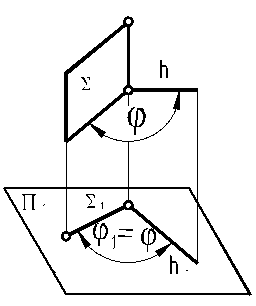
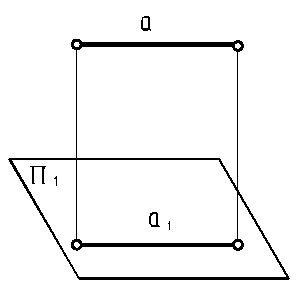
17. След проецирующей плоскости и проекции прямой, параллельной плоскости проекций, образуют угол, равный углу между прямой и плоскостью.	18. Проекции двух пересекаю-щихся или скрещивающих прямых, каждая из которых параллельна плоскости проекций, образуют угол, равный углу между этими прямыми.

Окончание таблицы 2

19. Проекция любой плоской фигуры, параллельной плоскости проекций, равна самой фигуре.

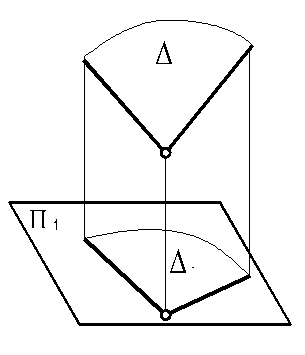
20. Проекция любой выпуклой плоской фигуры является тоже выпуклой.