Сортировка обменами
Классика жанра – это пузырьковая сортировка. Она же сортировка обменами, она же сортировка простыми обменами. Самая тормознутая, но зато самая простая и понятная.
Суть ее в том, что мы попарно сравниваем соседние элементы, и если последующий оказывается меньше предыдущего, то мы их меняем местами (отсюда и название). В результате одного такого прохождения по массиву максимальный элемент перемещается в его конец.
Посмотрим, как это происходит:
Пусть, дана некая последовательность B:
Берем первый и второй элементы, сравниваем их: 9>8, поэтому местами их менять не нужно. Далее берем 3-й и 2-й элементы: 1<9, поэтому выполняем обмен и т.д. Первое такое прохождение по массиву будет выглядеть следующим образом (показано состояние массива после выполнения i-го сравнения (и обмена, если он нужен)):
| Исходный массив | ||||||||
 1
| ||||||||
 3
| ||||||||
 9
| ||||||||
Таким образом, выполнив n-1 сравнений (обмены ведь были не при каждом сравнении), мы переместили максимум всего массива в конец. Далее берем в рассмотрение только оставшуюся часть массива – с 1-го по 7-й элемент, и проделываем с нею те же операции. И так до тех пор, пока в оставшейся части у нас не останутся только первый и второй элементы.
Алгоритм будет выглядеть так:
|
|
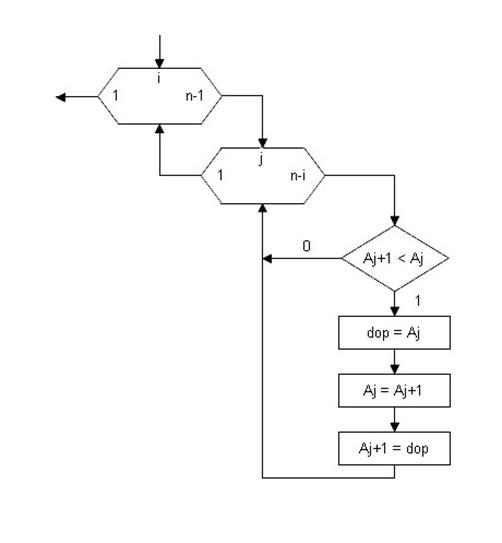
Внешний цикл – это количество полных прохождений по массиву.
Внутренний цикл – это однократное прохождение по массиву, в итоге чего максимум рассматриваемой части массива перемещается в ее конец.
Верхнюю границу значений внутреннего цикла можно поставить также n-1 – ошибкой это не будет, но тогда мы будем сравнивать те элементы на конце массива, которые и так уже будут упорядочены.
Еще более рациональный вариант – сделать все с использованием флажка. Если на каком-то этапе прохождения массива выяснится, что не было выполнено ни одного обмена, значит массив уже отсортирован, и можно выходить из цикла.
Вот как это будет выглядеть:
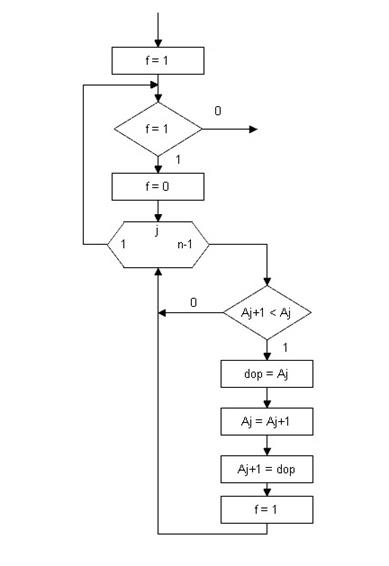
По сути, на этом все. Теперь просто разберемся, как это все сделать в коде (код написан по первому алгоритму – с использованием двух циклов).
for (i=1;i<n;i++)
for (j=0;j<n-i;j++)
if (b[j+1]<b[j])
{
dop=b[j];
b[j]= b[j+1];
b[j+1]=dop;
}
Сортировка простыми вставками
Как правило, понимание этого метода у большинства вызывает наибольшие трудности, но если разобраться в самой данного метода, то он уже не кажется таким уж страшным.
Пусть, имеется некоторая последовательность C из 7 элементов:
Словесно алгоритм сортировки простыми вставками (по возрастанию) выглядит так:
1. Первый элемент не трогаем.
2. Далее берем второй элемент, и смотрим: можно ли его вставить перед первым? 4 > 2, поэтому нельзя.
3. Берем следующий (3-й) элемент, и начинаем пытаться его впихнуть хоть перед кем-то из стоящих перед ним. Перед двойкой не пускают, перед четверкой тоже, так что сидим на месте.
|
|
4. Дошли до единицы (4-й элемент). Спрашиваем, можно ли ее поставить перед 2-ой? – Да, можно, т.к. 1<2. Задача вырисовывается следующая: все элементы от двойки до пятерки включительно надо сдвинуть вправо на одну позицию, а единицу поставить на место двойки.
5. Важно то, что при сдвиге этой последовательности (от 2 до 5) мы затираем 4-й элемент. Поэтому дабы его не потерять, сразу запоминаем в его дополнительную переменную:
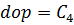
6. Далее при помощи цикла выполняем сдвиг последовательности:
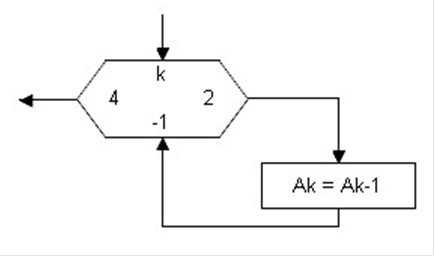
Ну, и наконец, поставим на место первого элемента нашу единицу:
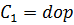
7. В итоге у нас получится следующее:
Так на каком мы там элементе остановились? – На 4-м. Но только теперь у нас на 4-м месте находится пятерка.
8. Далее берем 7-ку (5-й элемент), и снова начинаем "стучаться" к каждому из предыдущих элементов. Семерку мы никуда не засунем, поэтому переходим к 8-ке. - Ситуация аналогичная.
9. Добрались до 3-ки. Перед 1 и 2 не пущают, а вот перед четверкой можно стать. Как и в пунктах 5-6, запоминаем 3-ку в доп. переменную, сдвигаем последовательность {4, 5, 7, 8} на единицу вправо, и на место четверки ставим тройку.
На этом все и заканчивается. Теперь же, на основании приведенного выше словесного алгоритма, построим блок-схему (сл. стр.):
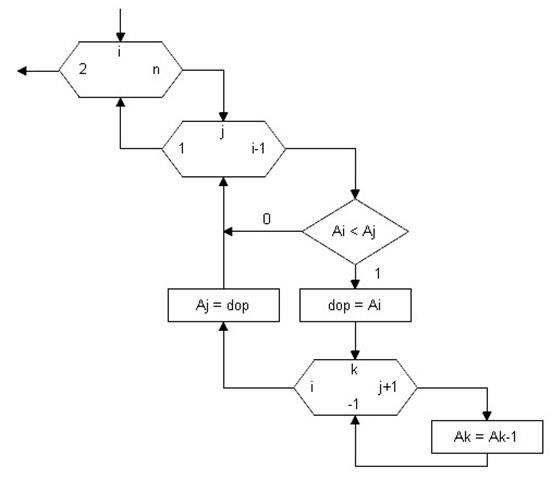
Внешний цикл у нас идет по i.
Вот, мы стоим на некотором элементе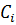 
, и начинаем терроризировать всех, стоящих перед ним, пытаясь вклиниться (цикл по j от 1 до i-1).
Если нужно выполнить сдвиг последовательности, и поменять местами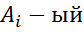 
элемент с 
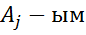, открываем цикл по k.
|
|
Теперь давайте посмотрим, как это все будет выглядеть в коде:
for (i=1;i<n;i++)
for (j=0;j<i;j++)
if (c[i]<c[j])
{
dop=c[i];
for (k=i;k>=j+1;k--)
c[k]=c[k-1];
c[j]=dop;
}
Вот такая вот конструкция и выполнит сортировку массива C методом простых вставок. Честно говоря, это не самый рациональный вариант этого алгоритма – есть и более оптимальные по скорости выполнения, а также удобству для понимания. Взял именно этот вариант потому, что он давался Светличной, а рассмотрение других способов лишь внесет путаницу.
Все три метода сортировок, выносимые на модуль, показаны в прилагаемом примере (в документах группы выложу исходник). Там одна и та же последовательность сортируется тремя методами.