Обработка результатов эксперимента.

 

Определение ошибки эксперимента.

 

Существует два способа определения ошибки эксперимента: по дисперсии параллельных опытов, то есть суммирования строки одной или ненулевого уровня и по суммированию каждой строки.

В данной работе используется первый способ, по суммированию нуле­вого уровня. Для этого проводится шесть опытов на нулевом уровне. Значения параметра оптимизации приводится в табл. 4.

Дисперсию определим по формуле /2/:

 

,

 

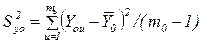где m₀ – число опытов.

Y_ou – значения параметров оптимизации в u – опыте,

- среднее значение параметра.

 

Ошибка эксперимента равна:

;

 

.

 

Расчёт коэффициентов уравнения регрессии

 

Метод ПФЭ позволяет получить зависимость параметра оптимизации от исследуемых факторов в виде полинома.

Коэффициенты вычисляем по формуле /2/:

:

где j – номер коэффициента уравнения

i – номер опыта

n = 16 – число опытов

 

Полученные коэффициенты записываются в табл.4.

 

Проверка значимости коэффициентов.

 

Существует два способа проверки значимости коэффициентов по крите­рию Стьюдента и по доверительному интервалу.

В данной работе используется второй способ, т.е. по доверительному ин­тервалу. Для этого находится дисперсия коэффициентов уравнения регрессии по формуле /2/:

 

Определяем доверительный интервал для коэффициентов по формуле /2/:

,

где S_bj – дисперсия уравнения регрессии,

t_a,f – коэффициент Стьюдента.

Коэффициент Стьюдента определяется из таблицы, в зависимости от ко­эффициентов f и a (при p=0,95 и f = 5), t = 2,57.

 

.

 

Условие значимости уравнения регрессии:

(коэффициент значим, все остальные коэффициенты пропадают)

В соответствие с условием, уравнение принимает вид:

 

(6)

 

2.1.4 Проверка модели на адекватность.

 

Проверка на адекватность проводится по критерию Фишера. Сначала находим дисперсию адекватности (7):

 

,

 

где – число оставшихся коэффициентов ( = 11);

y_i – экспериментальные значения;

ŷ_i – расчётные значения полученные по новому уравнению регрессии.

Для нахождения y_i в уравнение (7) подставляем значение (+ или к –) x_i, составляется таблица 5.

 

Таблица 5

Значимые коэффициенты и параметры для расчёта дисперсии адекватности.

i	b0	b1	b2	b4	b12	b14	b23	b24	b34	b124	b134	yi
1	11,62	3,89	0,93	-1,41	0,74	-1,03	-0,42	-0,28	-0,90	-0,48	-0,71	11,53	11,95	0,42
2	11,62	-3,89	0,93	-1,41	-0,74	1,03	-0,42	-0,28	-0,90	0,48	0,71	7,44	7,13	0,31
3	11,62	3,89	-0,93	-1,41	-0,74	-1,03	0,42	0,28	-0,90	0,48	-0,71	11,38	10,97	0,41
4	11,62	-3,89	-0,93	-1,41	0,74	1,03	0,42	0,28	-0,90	-0,48	0,71	7,48	7,19	0,29
5	11,62	3,89	0,93	-1,41	0,74	-1,03	0,42	-0,28	0,90	-0,48	0,71	16,42	16,01	0,41
6	11,62	-3,89	0,93	-1,41	-0,74	1,03	0,42	-0,28	0,90	0,48	-0,71	8,04	8,35	0,31
7	11,62	3,89	-0,93	-1,41	-0,74	-1,03	-0,42	0,28	0,90	0,48	0,71	12,97	13,35	0,38
8	11,62	-3,89	-0,93	-1,41	0,74	1,03	-0,42	0,28	0,90	-0,48	-0,71	6,46	6,73	0,27
9	11,62	3,89	0,93	1,41	0,74	1,03	-0,42	0,28	0,90	-0,48	0,71	21,93	21,57	0,36
10	11,62	-3,89	0,93	1,41	-0,74	-1,03	-0,42	0,28	0,90	-0,48	-0,71	8,22	7,87	0,35
11	11,62	3,89	-0,93	1,41	-0,74	1,03	0,42	-0,28	0,90	-0,48	0,71	17,21	17,55	0,34
12	11,62	-3,89	-0,93	1,41	0,74	-1,03	0,42	-0,28	0,90	0,48	-0,71	8,98	8,73	0,25
13	11,62	3,89	0,93	1,41	0,74	1,03	0,42	0,28	-0,90	0,48	-0,71	18,84	19,19	0,35
14	11,62	-3,89	0,93	1,41	-0,74	-1,03	0,42	0,28	-0,90	-0,48	0,71	7,99	8,33	0,34
15	11,62	3,89	-0,93	1,41	-0,74	1,03	-0,42	-0,28	-0,90	-0,48	-0,71	13,86	13,49	0,37
16	11,62	-3,89	-0,93	1,41	0,74	-1,03	-0,42	-0,28	-0,90	0,48	0,71	7,24	7,51	0,27

 

 

Определяем дисперсию адекватности:

 

;

 

Определение расчётного критерия Фишера:

 

 

Проверка на адекватность модели по критерию Фишера.

Если то модель адекватна.

f₁ = 5, f₂ =5, где f₁=N-k, f₂=m₀-1

F_табл =5,35

 

F_расч < F_табл (2,71<5,35), следовательно модель адекватна.