Энергия связи атомных ядер

Модуль 10. Основы физики атомного ядра

Основные формулы

Соотношение неопределенностей

Неопределенности координат и компонент импульса связаны соотношениями

ΔxΔp_x≥ћ, ΔyΔp_y≥ћ, ΔzΔp_z≥ћ,

где Δx – неопределенность координаты частицы; Δр – неопределенность импульса частицы (электрона); ћ – постоянная Планка, деленная на 2π.

Если электрон в атоме находится в возбужденном состоянии время Δt, то его энергия может быть определена с точностью ΔW, удовлетворяющей соотношению ΔWΔt≥ћ.

Радиоактивность

Основной закон радиоактивного распада: число нераспавшихся атомов в образце радиоактивного изотопа уменьшается со временем экспоненциально: N=N₀·e^–λt, где N – число нераспавшихся атомов в момент времени t; N₀ – число нераспавшихся атомов в момент, принятый за начальный (t = 0); е – основание натуральных логарифмов; λ – постоянная радиоактивного распада.

Число атомов, распавшихся за время t, N₀ – N=N₀(1–e^–λt).

Если промежуток времени Δt очень мал по сравнению с периодом полураспада Т_1/2, то для определения числа распавшихся атомов служит приближенная формула ΔN ≈ λNΔt.

Период полураспада Т_1/2 – промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением

.

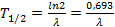Среднее время жизни τ радиоактивного нуклида – промежуток времени, за который число нераспавшихся атомов уменьшается в е раз: .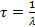

Число атомов, содержащихся в образце нуклида, 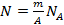, где m – масса образца; А – масса килограмм-атома нуклида; N_A – число Авогадро.

Активность а образца измеряется числом ядер, распавшихся в единицу времени: 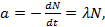или после замены N а = λN₀ e^–λt.

Активность образца в начальный момент (при t = 0) а₀ = λN₀.

Активность образца изменяется со временем по тому же закону, что и число нераспавшихся ядер: а=а₀ е^–λt.

Энергия связи атомных ядер

Дефект массы. Согласно релятивистской механике масса покоя М устойчивой системы взаимосвязанных частиц меньше суммы масс покоя m₁ + m₂ + … + m_k тех же частиц, взятых в свободном состоянии. Разность ΔМ = (m₁ + m₂ + … + m_k) – М называется

дефектом массы системы частиц.

Уменьшение массы покоя свободных частиц при соединенииих в устойчивую систему происходит вследствие освобождения некоторой части энергии покоя этих частиц. Выделившаяся энергия называется энергией связи.

Из закона сохранения энергии следует, что наименьшая энергия, которую нужно затратить, чтобы расчленить устойчивую систему взаимосвязанных частиц на отдельные свободные частицы, равна энергии связи.

Энергия связи прямо пропорциональна дефекту массы системы частиц ΔW = с²ΔМ, где с² – коэффициент перехода от массы к энергии, численно равный квадрату скорости света в вакууме; 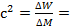8,987·10¹⁶ Дж/кг=8,987·10¹⁶ м²/с².

Если энергия выражена в мегаэлектрон-вольтах, а масса в атомных единицах, то с² = 931,44 МэВ/а.е.м.

Дефект массы ΔМ атомного ядра есть разность между суммой масс свободных протонов и нейтронов и массой образовавшегося из них ядра: ΔМ = (Ζm_p + Nm_n) – M, где Ζ – число протонов в ядре; N – число нейтронов (N = A – Ζ); m_p и m_n – массы свободных протона и нейтрона; М – масса ядра.

Ядерные реакции

Символическая запись ядерной реакции может быть дана или в развернутом виде, например 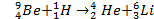, или сокращенно: ⁹Be (р, α) ⁶Li.

Обозначения частиц: e – электрон; p – протон; n – нейтрон; d – дейтрон; t – тритон; α – альфа-частица; γ – гамма-фотон.

При решении задач применяются законы сохранения:

– числа нуклонов А₁ + А₂ = А₃ + А₄;

– заряда Ζ₁ + Ζ₂ = Ζ₃ + Ζ₄;

– релятивистской полной энергии Е₁ + Е₂ = Е₃ + Е₄;

– импульса .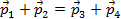

Энергетический эффект ядерной реакции Q=c²[(m₁ + m₂) – (m₃ + m₄)], где m₁ – масса покоя ядра-мишени; m₂ – масса покоя бомбардирующей частицы; m₃ + m₄ – сумма масс покоя ядер продуктов реакции.

Если m₁ + m₂ > m₃ + m₄, то энергия освобождается, энергетический эффект положителен, реакция экзотермическая.

Если m₁ + m₂ < m₃ + m₄, то энергия поглощается, энергетический эффект отрицателен, реакция эндотермическая.