Так как инвестиционный проект осуществляется в течение длительного периода времени, то необходимо учитывать фактор времени. Это связано с тем, что с течением времени ценность денег уменьшается (рубль инвестированный (полученный) сегодня стоит дороже, чем тот же рубль через год). Для соизмерения расходов и доходов, получаемых в различные периоды времени, используют их приведение (дисконтирование) к моменту начала проекта (в нашем случае к 1.01.2002г.). Дисконтирование осуществляется путем умножения расходов (доходов), произведенных в t -й момент времени на коэффициент дисконтирования a t:
, (2)
где е – ставка дисконта. Ставка дисконта задается: инвестором и равна доходности, которую он хотел бы получить на инвестированный капитал. Нет единого подхода к определению этой величины. Ставка дисконта обычно равна банковской ставке в наиболее надежных банках. Также ставка дисконта может соответствовать уровню доходности, который преобладает на рынке в момент анализа выгодности инвестиционных проектов [1]. В данной курсовой работе используется годовая ставка дисконта е =0,25.
Формула (2) справедлива при неизменной ставке дисконта. Если же ставка дисконта меняется во времени и на t -м шаге расчета равна et, то коэффициент дисконтирования равен
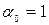и 
при t >0. (3)
В курсовой работе предполагается, что годовая ставка дисконта неизменна. Однако в отчетных таблицах 9-11 используются периоды времени различной продолжительности: месяц, квартал, год. Зная годовую ставку дисконта можно рассчитать ставку дисконта на квартал (
), на месяц (
). Таким образом, получаем, что при неизменной годовой ставке дисконта, ставка дисконта для некоторого периода времени изменяется в зависимости от длительности интервала времени. Например, коэффициент дисконтирования:
|
|
для 1.2002 ;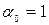
для 11.2002 
;
для второго квартала 2003 г. (4.2003-6.2003)
;
для 2004 г. 
.
Если расходы (доходы) были распределены равномерно в течение некоторого периода времени, то рекомендуется [14, 16] использовать коэффициент дисконтирования вида
и 
при t >0. (4)
В данной курсовой работе будем считать, что расходы и доходы распределены равномерно в пределах периода времени, поэтому необходимо использовать коэффициент дисконтирования (4). Тогда коэффициент дисконтирования:
для 1.2002 
;
для 11.2002 
;
для второго квартала 2003 г. (4.2003-6.2003)
;
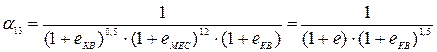для 2004 г. 
.
Коэффициенты дисконтирования a t Таблица 12
| at | |||
| Январь | 0,991 | ||
| Февраль | 0,972 | ||
| Март | 0,955 | ||
| 1 квартал | 0,778 | ||
| Апрель | 0,937 | ||
| Май | 0,920 | ||
| Июнь | 0,903 | ||
| 2 квартал | 0,736 | ||
| Июль | 0,886 | ||
| Август | 0,870 | ||
| Сентябрь | 0,854 | ||
| 3 квартал | 0,696 | ||
| Октябрь | 0,838 | ||
| Ноябрь | 0,823 | ||
| Декабрь | 0,807 | ||
| 4 квартал | 0,658 | ||
| ГОД | 0,572 |
Для оценки инвестиционных проектов рассчитывают следующие показатели:
1. NPV (Net Present Value) – чистый дисконтированный доход (ЧДД) [1].
, (5)
где Ф 1(t) – кэш-фло от операционной деятельности (Строка 3 Отчета о движении денежных средств); Ф 2(t) – кэш-фло от инвестиционной деятельности (Строка 6 Отчета о движении денежных средств); SЛ – дисконтированная ликвидационная стоимость предприятия.
Ликвидационная стоимость предприятия может определяться различными методами: на основе балансовой стоимости акционерного капитала по бухгалтерской отчетности; на основе рыночных сравнений [5], по стоимости замещения [5] и др. В [14] рекомендуется использовать так называемую модель Гордона. Она предполагает, что поток реальных денег Ф 1(t)+ Ф 2(t) за пределами инвестиционного проекта растет на g процентов в год. Тогда дисконтированная ликвидационная стоимость предприятия равна дисконтированной стоимости будущих потоков реальных денег за пределами проекта. В нашем случае
|
|
, (6)
где Ф 1(Т), Ф 2(Т) – соответствующие потоки реальных денег в последний год проекта.
В курсовой работе будем полагать, что g =0.
Если NPV <0, то проект не эффективен. Чем NPV больше, тем эффективнее проект.
2. IR – индекс доходности (ИД) [2]
, (7)
где К – дисконтированные инвестиции,
(8)
Если IR <1 – проект не эффективен. Если IR ³1, проект рентабелен.
3. IRR (Internal Rate of Return) – внутренняя норма доходности (ВНД) [3] представляет собой ту ставку дисконта е, при которой величина NPV равна 0.
Если рассматривать NPV как функцию от ставки дисконта е, то примерный график функции приведен на рис. 1.
Иными словами, IRR является решением уравнения
NPV (IRR)=0. (9)
Рассчитанная величина нормы доходности сравнивается с требуемой инвестором величиной нормы доходности на капитал.
Если IRR ³ е, то проект считается эффективным.
 |
Рис.1
Замечание. Чтобы найти IRR, необходимо решить нелинейное уравнение (9). Для этого выполняют несколько пробных расчетов при различных значениях показателя IRR. Например, для IRR равного 0.2, 0.4 или при других значениях. Так как такие вычисления являются достаточно трудоемкими, для приближенного вычисления IRR можно использовать метод линейной аппроксимации. Для этого выбирают два таких значения ставки дисконта е 1 и е 2, чтобы в интервале (е 1, е 2) функция NPV (e) меняла свой знак с "+" на "–" или с "–" на "+". Далее применяют формулу
|
|
. (10)
Для получения приемлемой точности оценки IRR делают несколько итераций, пока не достигнут приемлемой точности. В данной курсовой работе итерационный процесс вычисления IRR прекратите, если на очередной итерации длина интервала (е 1, е 2) меньше 0,01.
4. PP (Payback Period) – cрок окупаемости инвестиций. - это срок, за который можно возвратить инвестированные в проект средства.
Приведем пример расчета интегральных показателей инвестиционного проекта. Период инвестирования Т=4 года. Ставка дисконта е =0,15, g =0,05=5%.
Будем предполагать, что поток реальных денег в t -м году проекта распределен равномерно в пределах года. Для простоты при дисконтировании элементов денежного потока будем считать, что оттоки и притоки приходятся на середину года.
Таблица 13
| № | Шаги расчета, t | 01.2002 | 02.2002 | 03.2002 | 04.2002 | 05.2002 | 06.2002 | 07.2002 | 08.2002 | 09.2002 | 10.2002 | 11.2002 | 12.2002 | 1кв.2003 | 2кв.2003 | 3кв.2003 | 4кв.2003 | |
| Кэш-фло от операционной деятельности Ф 1(t) | -542,423 | -542,423 | -681,023 | -616,975 | 182,733 | 265,588 | 342,127 | 418,666 | 505,059 | 512,619 | 520,179 | 520,179 | 1497,621 | 1497,621 | 1497,621 | 1497,621 | 5896,109 | |
| Кэш-фло от инвестиционной деятельности Ф 2(t) | -100,000 | -1250,000 | -1750,000 | -350,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | |
| Поток реальных денег Ф 1(t)+ Ф 2(t) | -642,423 | -1792,423 | -2431,023 | -966,975 | 182,733 | 265,588 | 342,127 | 418,666 | 505,059 | 512,619 | 520,179 | 520,179 | 1497,621 | 1497,621 | 1497,621 | 1497,621 | 5896,109 | |
| Коэффициенты дисконтирования at | 0,991 | 0,972 | 0,955 | 0,937 | 0,920 | 0,903 | 0,886 | 0,870 | 0,854 | 0,838 | 0,823 | 0,807 | 0,778 | 0,736 | 0,696 | 0,658 | 0,572 | |
| Дисконтированный поток реальных денег [ Ф 1(t)+ Ф 2(t)]× at | 0,991 | 0,972 | 0,955 | 0,937 | 0,920 | 0,903 | 0,886 | 0,870 | 0,854 | 0,838 | 0,823 | 0,807 | 0,778 | 0,736 | 0,696 | 0,658 | 0,572 | |
Кумулятивный дисконтированный чистый поток реальных денег 
| -636,477 | -1743,118 | -2320,595 | -906,045 | 168,065 | 239,768 | 303,176 | 364,166 | 431,219 | 429,610 | 427,914 | 420,031 | 1165,140 | 1101,921 | 1042,133 | 985,589 | 3375,130 | |
| Ф2(t) – кэш-фло от инвестиционной деятельности× at | 99,075 | 1215,616 | 1670,508 | 327,946 |
=12075,231
=16922,857
К=3313,144
IR=6,108
По данным о кумулятивном дисконтированном чистом потоке реальных денег (рис. 2) можно сделать вывод, что срок окупаемости лежит в диапазоне от 2 кв. 2003г. до 3кв. 2003г. лет.
Рисунок 2.
Методом линейной интерполяции можно уточнить срок окупаемости
PP=2,74 года.
Замечание. В рамках данной работы можно применить приближенный метод нахождения IRR. Для этого при расчете NPV не будем использовать значение ликвидационной стоимости S Л. Таким образом, при ставке дисконта е =0,25 и без учета S Л значение NPV (0,25)=4676,740. Необходимо найти значение NPV при ставке дисконта е =0, т.е. без учета дисконтирования. Для этого используем данные о потоке реальных денег.
NPV (0)= 9320,902
На основании этих данных построим график (рис. 3), проведя прямую через точки NPV (0) и NPV (0,25). Абсцисса точки пересечения данной прямой с осью абсцисс даст приближенную оценку IRR=52,09 %.
IRR=52,09%
Инвестиционный проект Б
Изучение данного варианта инвестирования является достаточно простым для анализа, поэтому произведем расчет только интегральных показателей эффективности инвестиций.
Положив в банк 1.01.2002 сумму S под i% годовых, через три года 1.01.2005 мы снимем с банковского счета некоторую сумму денег. Произведем расчет этой суммы.
К 1.01.2003 на депозите будет находиться сумма S ´(1+ i /100). Таким образом, прирост денежных средств за год составит S ´ i /100. Однако с процентных доходов по вкладам в банках необходимо уплачивать налог на доходы физических лиц по ставке 13%. В рамках работы будем полагать, что налогом облагается доход по вкладам в банках в части превышения суммы, рассчитанной исходя из 20 % годовых. Следовательно, на 1.01.2003 в банке с учетом уплаты налога будет числиться сумма S ´(1,07+0,65 i /100). Если в течение трех лет мы не будем снимать деньги с депозита, то в итоге по прошествии трех лет на счете будет числиться сумма S ´(1,07+0,65 i /100)3, так как при начислении процентов используется формула сложных процентов [1, 8, 9]. Тогда
Ф 1(0)=0, Ф 2(0) = – S;
Ф 1(t)= Ф 2(t) =0 при 0 < t < T,
Ф 1(T) = S ´(1,07+0,65 i /100)3, Ф 2(T)=0.
Отсюда
. (11)
NPV=-5000+(5000*(1,07+0,65*46/100)3/(1+0,25)3=7631,268
Здесь использован коэффициент дисконтирования вида (2), так как помещение денег в банк и изъятие вклада являются операциями, производимыми в некоторый момент времени.
Найдем IRR, решив уравнение (11) при NPV =0:
IRR= 0,07+0,65 i /100=0,07+0,65*46/100=0,369. (12)
Очевидно, что дисконтированные инвестиции К = S. Найдите IR, воспользовавшись формулой (7).
IR=1+7631,268/5000=2,526
Срок окупаемости PP для простоты будем считать равным 3 годам.