1. На диаграмме изображён среднемесячный курс евро в период с октября 2013 года по сентябрь 2014 года. По горизонтали указываются месяц и год, по вертикали — курс евро в рублях.

| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ КУРСА ЕВРО | |
| А) октябрь−декабрь 2013г. Б) январь–март 2014г. В) апрель–июнь 2014г. Г) июль–сентябрь 2014. | 1) содержит месяц с наибольшим курсом евро за период с октября 2013 года по сентябрь 2014 года 2) содержит месяц с наименьшим курсом евро за период с октября 2013 года по сентябрь 2014 года 3) среднемесячный курс евро падал все месяцы периода 4) в последний месяц периода средний курс евро был больше 48 рублей и меньше 50 рублей за 1 евро |
2. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.
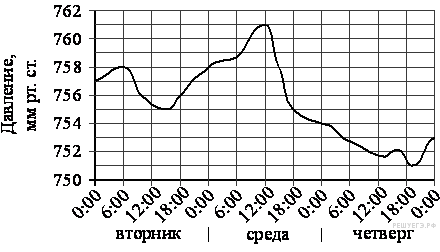
Пользуясь диаграммой, установите связь между промежутками времени и характером изменения давления.
| ПРОМЕЖУТКИ ВРЕМЕНИ | ХАРАКТЕР ИЗМЕНЕНИЯ ДАВЛЕНИЯ | |
| А) 06:00−18:00 вторника Б) 00:00−18:00 среды В) 12:00−18:00 среды Г) 18:00−00:00 cреды | 1) Давление сначала увеличивалось, затем уменьшалось 2) Давление сначала уменьшалось, затем увеличивалось 3) Давление уменьшалось медленнее всего 4) Давление уменьшалось быстрее всего |
3. На графике изображена зависимость скорости движения легкового автомобиля от времени. На вертикальной оси отмечена скорость легкового автомобиля в км/ч, на горизонтальной — время в секундах, прошедшее с начала движения автомобиля.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автомобиля на этом интервале.
| ИНТЕРВАЛЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) 0–30 c Б) 30–60 c В) 90–120 c Г) 120–150 c | 1) автомобиль ехал с постоянной скоростью больше 15 секунд 2) скорость автомобиля сначала увеличивалась, а потом уменьшалась 3) автомобиль увеличивал скорость на всём интервале 4) автомобиль ровно 15 секунд ехал с постоянной скоростью |
4. На рисунке изображён график функции y = f (x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной.
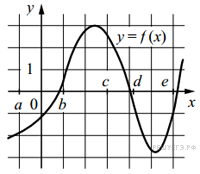
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ | |
| А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) | 1) производная отрицательна на всём интервале 2) производная положительна на всем интервале 3) функция отрицательна на всем интервале 4) функция положительна на всём интервале |
5. На рисунке изображён график функции, к которому проведены касательные в четырёх точках.
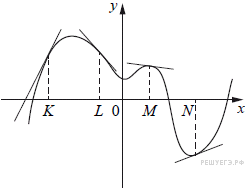
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ | |
| А) K Б) L В) M Г) N | 1)  2) 2
3)
2) 2
3) 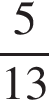 4)
4) 
|
6. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.
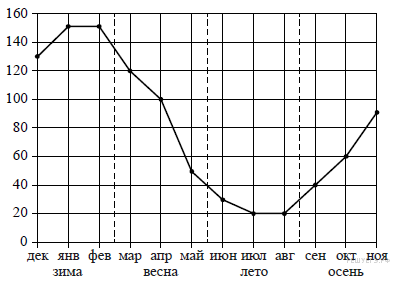
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) зима Б) весна В) лето Г) осень | 1) Ежемесячный объём продаж был меньше 40 штук в течение всего периода. 2) Ежемесячный объём продаж достиг максимума. 3) Ежемесячный объём продаж падал в течение всего периода. 4) Ежемесячный объём продаж рос в течение всего периода. |
7. На графике показана зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в H · м.

Пользуясь графиком, поставьте в соответствие каждому интервалу количества оборотов двигателя характеристику зависимости крутящего момента двигателя на этом интервале.
| ХАРАКТЕРИСТИКИ ПРОЦЕССА | ИНТЕРВАЛЫОБОРОТОВ | |
| А) крутящий момент не менялся Б) крутящий рос быстрее В) крутящий момент падал Г) крутящий момент не превышал 20 H · м | 1) 0 − 1500 об/мин. 2) 2000 − 3000 об/мин. 3) 3000 − 4000 об/мин. 4) 4000 − 6000 об/мин. |
8. На диаграмме изображены дневные среднемесячные температуры воздуха в Москве по данным многолетних наблюдений. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
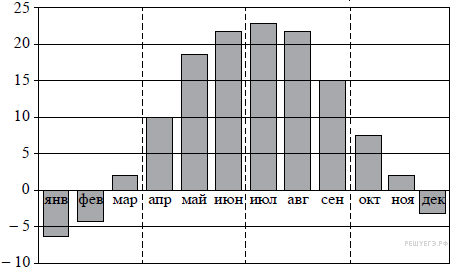
Пользуясь диаграммой, поставьте в соответствие каждому из указанных периодов времени характеристику температуры.
| ИНТЕРВАЛЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ | |
| А) 1-й квартал года Б) 2-й квартал года В) 3-й квартал года Г) 4-й квартал года | 1) средняя температура за каждый месяц квартала не ниже 13°С 2) средняя температура за последний месяц квартала более чем на 10 градусов превышает среднюю температуру за первый месяц квартала 3) средняя температура за последний месяц квартала отрицательная 4) ровно два месяца квартала средняя температура отрицательная |
9. На рисунке изображён график функции y = f (x) и отмечены точки A, B, C и D на оси x. Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и её производной.
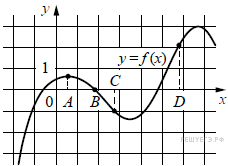
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ | |
| А) A Б) B В) C Г) D | 1) Функция положительна, производная равна 0. 2) Производная отрицательна, функция равна 0. 3) Производная положительна, функция положительна. 4) Функция отрицательна, производная отрицательна. |
Выберите любое из предложенных заданий и решите его.
0. На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 22 литра бензина по цене 33 руб. 20 коп. за литр. Сколько рублей сдачи он должен получить у кассира?
Задание №15. Задачи по планиметрии.
1. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
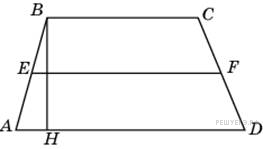
2. В треугольнике 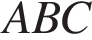 угол
угол 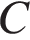 равен 90°,
равен 90°,  ,
,  . Найдите
. Найдите  .
. 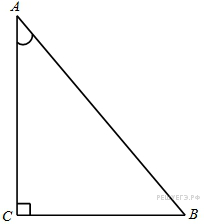
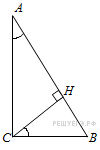
3. В треугольнике ABC угол C равен 90°, CH — высота,  ,
, 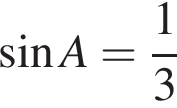 . Найдите BH.
. Найдите BH.
4. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

5. В треугольнике 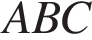 угол
угол 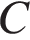 равен 90°,
равен 90°,  . Найдите синус внешнего угла при вершине
. Найдите синус внешнего угла при вершине 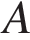 .
.

6. В треугольнике 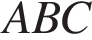 угол
угол 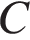 равен 90°,
равен 90°,  ,
, 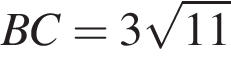 . Найдите
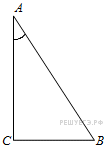
. Найдите  .
. 
7. В треугольнике 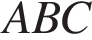 угол
угол 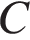 равен 90°,
равен 90°,  ,
,  . Найдите
. Найдите 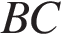 .
.
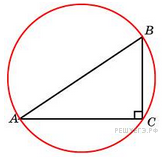
8. В треугольнике 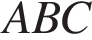
 , угол
, угол 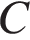 равен 90°. Радиус описанной окружности этого треугольника равен 5. Найдите
равен 90°. Радиус описанной окружности этого треугольника равен 5. Найдите 
. 
9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
10. В треугольнике 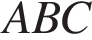 угол
угол 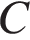 равен 90°,
равен 90°, 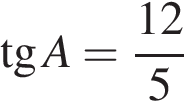 ,
,  . Найдите
. Найдите 
. 