Многоэкстремальные задачи оптимизации

Власов М. П.

 

конспект лекций по дисциплине
Оптимальное управление экономическими системами

Только себе и бесплатно

 

ТЕМА № 6

Множественность оценок при оптимизации

 

для студентов специальности ……. всех форм обучения

 

Содержание

Стр.

1.Взаимные задачи как метод моделирования сложных систем ….……….. 2

2.Методология поиска компромиссных управленческих решений:
многоцелевая оптимизация …………………..……………………………….. 6

3.Векторная оптимизация ……………………………………………………. 10

4.Метод последовательных уступок …………………………………….…... 15

5.Метод минимизации суммы относительных
степеней достижения цели …………………………………………………… 16

6.Метод минимизации равных относительных
степеней достижения цели …………………………………………………… 17

7.Метод максимизации минимальной относительной степени
достижения цели.……………………..……………………………………… 17

8.Многоэкстремальные задачи оптимизации ……………………………….. 24

Литература …………………………………………………………………….. 29

Санкт-Петербург 2002-6

 

1. Взаимные задачи как метод моделирования сложных систем

Взаимные оптимизационные задачи – это пара задач скалярной оптимизации народнохозяйственного плана, в которых с разных сторон отыскивается наилучшее распределение дефицитных ресурсов. Максимизируемая в одной из задач целевая функция образует ограничивающее условие (ограничение) для другой. И наоборот, минимизируемая целевая функция второй задачи служит ограничением для первой задачи.

Суть использования аппарата взаимных задач кратко можно сформулировать следующим образом.

Исходная задача (обозначим ее А) заменяется при необходимости по специальным правилам на соответствующую ей взаимную задачу (задача В); решение же последней позволяет отыскать оптимальный план исходной задачи.

Теория взаимных оптимизационных задач имеет в экономико-математическом моделировании разнообразное применение. Нередко оказывается, что задачи, являющиеся взаимными, принадлежат разным классам задач математического программирования (например, А – задача квадратического программирования, а В – линейного). Тогда решение более сложной задачи можно свести к решению задачи более простой математической структуры.

Достаточно часто целевые функции конкретных моделей не могут быть выражены в аналитическом виде, т. е. количественно. В этом случае использование теории взаимных задач может обеспечить решение такой не решаемой обычными методами модели.

Понятие взаимных задач, кроме того, позволяет установить эквивалентность двух основных модификаций оптимизационных экономико-математических моделей: максимизации результата (конечной продукции) при ограниченных ресурсах и минимизации затрат ресурсов на производство заданного объема конечной продукции. Преимущества же критерия минимизации затрат ресурсов очевидны: измерение затрат на производство различных продуктов и услуг является гораздо более легкой задачей, чем систематизация наборов экономических благ по их общественному полезному эффекту. Решение народнохозяйственных задач с рассматриваемым критерием позволяет оценивать эффективность тех или иных хозяйственных мероприятий величиной сэкономленных затрат, т. е. оперировать привычными показателями, широко используемыми в локальных экономических расчетах.

Рассмотрим основные положения теории взаимных задач, как в общем виде, так и проиллюстрирована на конкретном числовом примером.

Исходная задача А может быть записана в этом случае следующим образом:

Общий вид задачи	Конкретная модель
,	,
,
.	.

 

Из множества всех видов используемых ресурсов выделим дефицитные ресурсы. Ресурс называется дефицитным, если любое изменение его количества ведет к изменению оптимального значения целевой функции модели. Вопрос о выделении из всего множества используемых в модели ресурсов устойчиво дефицитного решается в каждом конкретном случае на качественном концептуальном уровне. В масштабе, например, народного хозяйства в целом таким ресурсом может являться труд.

Исключительное положение трудовых ресурсов среди всех других ресурсов объясняется рядом причин.

Во-первых, количество трудовых ресурсов в каждый данный момент времени ограничено, и их увеличение мало зависит от развития экономики (почти не зависит в пределах 15-летнего планового периода).

Во-вторых, трудовые ресурсы являются наиболее универсальным ресурсом, так как относительный избыток трудовых ресурсов в одной какой-нибудь сфере деятельности может быть направлен в другие сферы деятельности.

В-третьих, в рационально и справедливо организованном обществе одним из важнейших факторов повышения благосостояния и развития членов общества является увеличение свободного времени трудящихся за счет сокращения рабочего времени (свободное время является компонентом вектора, на котором определяется целевая функция благосостояния экономической системы).

Поэтому экономия труда (в отличие от экономии других производственных ресурсов) не только создает предпосылки для ускорения развития экономики страны, но и может непосредственно увеличивать уровень благосостояния населения страны.

Замечательным свойством дефицитного ресурса i _деф является его полное использование в оптимальном плане x _opt, что обращает неравенство g_{i деф} (x) £ b_{i деф} в строгое равенство.

Выделим из всех ограничивающих условий для специального рассмотрения ограничение по одному (любому) дефицитному ресурсу и обозначим его h (x) £ а, подчеркнув еще раз, что h (x _opt) = a. Тогда исходная задача А запишется следующим образом:

В общем виде	Конкретная модель
,	,
,
,
.	.

 

Обозначим оптимальное значение целевой функции исходной задачи и сформулируем условия* перехода от исходной задачи А к взаимной по отношению к ней задаче В.

1. Зафиксировать оптимальное значение целевой функции исходной задачи А и ввести ограничение в систему ограничений взаимной задачи В.

2. В качестве минимизируемой целевой функции взаимной задачи В взять функцию затрат дефицитного ресурса исходной задачи А.

Тогда задача В (взаимная) запишется следующим образом:

В общем виде	Конкретная модель
,	,
,
,
.	.

 

Решение взаимной задачи В, как следует из вышеизложенного, предполагает знание в общем случае априори неизвестного максимально достижимого уровня целевой функции исходной задачи А. Однако теория взаимных задач позволяет решать соответствующие задачи в итеративном режиме параметрического программирования относительно возрастающего параметра .

Укрупненный алгоритм расчета может быть при этом следующим.

1. Экспертным путем (либо на основании опыта лица, принимающего решения) задается первоначальная оценка оптимального значения целевой функции исходной задачи .

2. Решается взаимная задача В, в результате отыскивается ее оптимальный план .

3. С использованием замечательного свойства дефицитного ресурса осуществляется проверка найденного в п. 2 решения на оптимум (исходной задачи). Признаком его нахождения будет выполнение строгого равенства , т. е. полное использование дефицитного ресурса. В этом случае и процесс решения заканчивается. В противном случае – переход к п. 4.

4. Корректировка оценки оптимального значения целевой функции исходной задачи и переход к п. 2.

Очевидно, что реализация четвертого этапа алгоритма долж­на обеспечивать максимальную эффективность работы алгоритма с точки зрения его сходимости к оптимальному решению. Скорость сходимости алгоритма является одним из важнейших показателей качества экономико-математических моделей: обычно она оценивается количеством итераций, необходимых для получения искомого решения.

Читателям пособия предлагается самостоятельно найти оптимальный план исходной задачи, решив взаимную задачу, начиная с первоначальной оценки 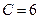. Решение провести графически, предложив концепцию корректировки с целью повышения скорости сходимости алгоритма.

2. Методология поиска компромиссных управленческих решений: многоцелевая оптимизация

Право, такое затруднение – выбор. Если бы еще один, два человека, а то четыре. Как хочешь, так и выбирай... Если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности у Балтазара Бал­та­за­ровича, да, пожалуй, прибавить к этому еще дородности Ивана Павловича – я бы тогда тотчас же решилась.

Н. В. Гоголь, «Женитьба»

До сих пор рассматривалось принятие оптимальных решений, в результате которых значения переменных придают целевой функции оптимальное значение с точки зрения одного какого-либо критерия. Чаще всего, а практически всегда, приходится принимать управленческие решения в более сложных ситуациях с учетом нескольких критериев одновременно.

Действительно, эффективность функционирования экономических систем любой степени сложности оценивается целым кортежем технико-экономических показателей. Любой студент сумеет перечислить не менее десятка из них и даже объяснить, чем каждый из них плох или чем хорош. В этих условиях совершенно очевидно, что относительно высокое значение одного или даже нескольких показателей в таких системах вовсе не означает, что эти экономические системы работают лучше других, так как уровень остальных показателей у них может быть ниже, чем в других системах. Рис. 2.1, приведенный ниже, со всей убедительностью это подтверждает.

Трудность выбора решения в условиях многоцелевой оптимизации определяется не столько количеством критериев оптимизации и, тем более, вариантов решения, сколько их противоречивостью: например, стремление к максимизации объема выпуска продукции одновременно ведет к суммарному росту ее себестоимости. Подобные противоречия имеют место и в отношении любых других частных (локальных) критериальных показателей.

Классическим примером такого противоречия, в тисках которого человечество бьется сотни лет, являются категории эффективность и социальная справедливость. Рыночная система, для которой характерна относительно высокая эффективность, может довольно хорошо обеспечить семью, живущую за чертой бедности (по сравнению с менее эффективной экономикой), однако семье миллионера она дает несравненно больше. Многие, кстати, считают такое положение вещей величайшей несправедливостью, которая не может быть оправдана никакой эффективностью.

Рис. 2.1. Иллюстрация проблемы многоцелевой оценки функционирования экономических систем

Конечно, математическое моделирование само по себе не может дать никаких рецептов правильного соотношения справедливости и эффективности, но с его помощью всегда можно определить, какие последствия для эффективности, а стало быть, и для социальной справедливости может иметь то или иное решение. Очень хорошо по этому поводу сказал Гете: «Цифры не управляют миром, но они показывают, как это делается ».

До появления методов многоцелевой оптимизации, когда приходилось сталкиваться с проблемой многокритериальности, все критерии, кроме одного, фиксировались и принимались в качестве ограничений, так что оптимизация производилась по одному из них, который признавался доминирующим. Такая постановка вопроса по сути дела означала уход специалиста от проблемы, и лицо, принимающее решение, оставалось один на один со сложной комбинаторной проблемой фиксации и варьирования множеством ограничений математической модели. Таким образом, стала совершенно очевидной потребность в более тонком подходе к многокритериальным проблемам, в использовании для этой цели аналитических моделей и методов.

Приступая к их рассмотрению, отметим, что в условиях естественной противоречивости критериев оптимальности, когда, в общем случае, невозможно обеспечить оптимальные значения по всем критериям одновременно, возникает желание найти такой план, для которого была бы в определенном смысле наилучшей совокупность этих значений по всем критериям вместе взятым. Такие планы называют оптимальными компромиссными.

Редко кто из молодых людей не морщит лоб при слове «компромисс», кто нейтрально произносит словосочетание «меньшее зло», ведь компромисс – это сделка, соглашение на основе взаимных уступок. Между тем, искусство разумного компромисса – это сама жизнь. Правда, «область применения» его небезгранична*. Сфера его приложения – скорее «нормальное» состояние экономической системы, например, общества в целом. Но если экономическая система требует радикальной трансформации, она не нуждается в услугах компромисса. Напротив, она ищет источник энергии в бескомпромиссности.

Идею поиска оптимального компромиссного плана рассмот­рим на простейшем примере оптимизации двумерного критерия f (x) = { f ₁(x), f ₂(x)} ® max, каждая составляющая которого представляет функцию от одной переменной х, определенной на некотором закрытом интервале [ a, b ]. Графики изменения составляющих f ₁(x) и f ₂(x) представлены на рис. 2.2.

Очевидно, что поиск оптимального компромиссного плана в данном конкретном примере целесообразен лишь на множестве точек интервала [ c, d ], так как вне этого интервала решение может быть улучшено сразу по обеим целевым функциям. План х ₁ будем считать лучше (предпочтительнее) плана х ₂ и обозначать х ₁ х ₂, если хотя бы по одной компоненте целевой вектор-функции f_s (x ₁) > f_s (x ₂), а по остальным компонентам f_s (x ₁) ³ f_s (x ₂). Это так называемое улучшение по Парето*, формулируемое очень просто: Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит кому-то пользу (по их собственным оценкам), является улучшением.

Рис. 2.2. Иллюстрация определения оптимального
компромиссного плана:

– компромиссная область

Интервал носит название множества Парето, или множества эффективных планов, и характеризуется теми важными свойствами, что на нем ни одно решение не может быть улучшено ни по одному из критериев без ущерба для других критериев.

Таким образом, множество Парето – это множество допустимых планов, ни один из которых не может быть улучшен:

.

Множественность эффективных планов является следствием «взаимозаменяемости» (взаимокомпенсации) скалярных критериев, позволяющей увеличивать одни компоненты за счет уменьшения других. В этих условиях каждый эффективный план по-своему исчерпывает возможность оптимизируемой экономической системы, реализуя определенный компромисс между частными целями. Таким образом, если принципы выделения множества эффективных планов строго научны, не требуют какого-либо постулирования и, следовательно, лишены элементов произвола и субъективизма, то определение на этом множестве оптимального компромиссного плана требует постулирования той или иной схемы компромисса.

Многие специалисты считают поэтому, что более эффективно было бы предоставить лицу, принимающему решение (ЛПР), полное множество эффективных планов, по которым ЛПР на основании имеющегося опыта, здравого смысла и других, не поддающихся формализации процедур, выберет единственное решение. Реализация такого подхода на практике сопряжена, однако, с серьезными методологическими трудностями, вызванными, прежде всего, отсутствием в настоящее время достаточно простых и ясных процедур построения эффективного множества (при количестве целевых функций ), а также сложностью его представления лицу, принимающему решение. Рассмотрим теоретическое обоснование многокритериальной или векторной оптимизации.

3. Векторная оптимизация

Векторная или многоцелевая оптимизация представляет направление в теории принятия решений, изучающее принятие решений по многим целевым функциям в планировании (проектировании). В отличие от формально идентичных задач принятия решений в других областях приложений (игры против природы, арбитражные и другие задачи), здесь все целевые функции заданы, а не выбираются случаем, но, как правило, неодинаковы по важности.

На практике, кроме целевых функций, характеризующих качество планов с разных, обычно противоречивых сторон, имеется представление о глобальном качестве различных планов. Однако это представление изменяется от задачи к задаче и трудно выделить какие-либо их классы, где оно было бы единым и формализуемым. С другой стороны, хотя представление о совокупном оптимуме порой весьма расплывчато, ценой дополнительных издержек (или риска) можно осуществит сравнение планов и определить, какой из них более приемлем для принимающего решение.

Эти особенности задач векторной оптимизации обусловили ее содержание и методы. Значительная часть подходов, используемых в принятии решений по многим целевым функциям, состоит в применении некоторых процедур принятия решений. При этом под процедурой понимается последовательное отсечение неоптимальных альтернатив на основе дополнительной информации, получаемой в ходе специально построенного эксперимента (расчетов). В целом такие процедуры похожи на процедуры проверки статистических гипотез, только критические области строятся не на основе апостериорных вероятностей, а при помощи каких-либо принципов оптимальности. Применяемые на отдельном шаге процедуры, принципы оптимальности обычно являются некоторыми упрощениями принципов для одношаговых задач, в остальном же от них не отличаются.

Задача векторной оптимизации приобретает характер математической, оптимизационной задачи, когда указан строгий смысл векторного оптимума, т. е. принципа оптимальности. В многоцелевых задачах, как и в других задачах принятия решений, принципы оптимальности могут формулироваться в виде некоторых упорядочений на множестве альтернатив, либо функций полезности, либо каких-то функционалов от целевых функций, подлежащих максимизации. Все три вида в известном смысле эквивалентны, и выбор одного из них связан с выбором математической техники для анализа задач. Наиболее логически стройная теория векторной оптимизации получена на основе применения методов теории полезности.

Полезностный подход можно охарактеризовать следующим образом. Если ест желание построить совокупную (глобальную) функцию полезности, то сначала должны позаботиться о ее существовании. Теория полезности дает необходимые и достаточные условия существования, тем самым указывая объем необходимой информации и характер предположений. Далее, пользуясь теоремами о виде функций полезности многокомпонентных альтернатив (компонентам соответствуют свои целевые функции), можно установить, как эта функция выражается через заданные целевые функции, определяющие полезность альтернатив по различным компонентам. Неизвестные параметры совокупной целевой функции определяются эмпирически, экспериментально либо экспертным путем. Установить вид функции удается лишь в случае, когда компоненты в определенном смысле независимы. Тем не менее, в число решаемых таким методом задач попадает много практически важных многоцелевых задач.

Базовой информацией в задаче векторной оптимизации является множество альтернатив 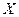и целевые функции

, ,

где - множество действительных чисел. Если никакой дополнительной информации нет, то обоснованным является лишь принцип оптимальности по Парето. Альтернатива называется оптимальной по Парето, если нет другой такой альтернативы , что для всех и хотя бы для одного неравенство строгое. Это означает, что оптимальное по Парето решение нельзя улучшить ни по одному признаку (целевой функции), не ухудшив при этом по какому-либо из остальных.

Вычислительные методы нахождения оптимальных по Парето альтернатив основываются на следующих фактах. Если 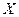выпукло и вогнуты, а - оптимальная по Парето альтернатива, то существуют такие числа , , что

. (3.1.)

Наоборот, если (3.1.) имеет место и все числа , то альтернатива - оптимальна по Парето при любых 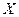и . Таким образом, варьируя веса можно находить все оптимальные по Парето альтернативы.

На тех же принципах основано большое число эвристических методов векторной оптимизации: эксперты определяют веса , отражающие важность целей , и найденная по (3.1.) альтернатива считается оптимальной.

Еще один метод нахождения оптимальных по Парето альтернатив можно строить на основе следующего утверждения. Если , и - оптимальна по Парето, то существуют такие числа , , что

. (3.2.)

Обратное утверждение также верно, однако, найденная по (3.2.) альтернатива может не быть строго оптимальной по Парето, если она попадает на такую часть границы 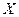, где для некоторого . В этом случае решение можно улучшить по .

Функционалы (3.1.) и (3.2.) позволяют находить все оптимальные по Парето альтернативы, однако не дают основания для выбора одной из них в качестве оптимального решения задачи векторной оптимизации. Даже в том случае, когда эксперты дают веса , или веса как-то определяются экспериментально, найденную альтернативы можно считать оптимальным решением лишь в случае, когда функционал представляет собой глобальную целевую функцию, т.е. функционал полезности для упорядочения (не строгое предпочтение) на 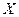, которое должно быть задано в дополнение к функциям .

В векторной оптимизации само упорядочение на 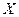обычно не задается, известными считаются лишь те или иные ее свойства. Среди обязательных свойств – согласованность с заданными целевыми функциями : если для некоторых и всех выполняются неравенства , то , причем отношение строгое, (т.е. , но не ), если хотя бы одно неравенство строгое. Другие свойства (аксиомы) векторной оптимизации:

· аддитивность: если и 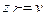, то для любого числа , , должно быть ;

· непрерывность: если , то для всех из окрестности ;

· сдвиг начала координат: если , то для некоторого (или всех) .

Сравнительно хорошо рассмотрен случай многокомпонентных альтернатив, т.е. случай, когда . В предположении, что компоненты в каком-либо смысле независимы по упорядочению на 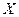(например, упорядочение на , индуцированное упорядочением на 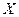при фиксированных , не зависит от этих ), получается глобальная функция аддитивного или мультипликативного вида.

Другой способ задания дополнительной информации о глобальном упорядочении альтернатив – задание упорядочения (частичного) на множестве признаков (целевых функций) по важности признаков. Дополнительная информация о том, какой признак важнее, отсекает часть глобальных по Парето альтернатив как неоптимальных глобально. Если информация настолько «богата», что позволяет построить функцию полезности признаков, то получим глобальную целевую функцию и единственное глобальное оптимальное решение (или некоторое множество эквивалентных ему).

С учетом этого на практике пользуются обычно некоторым набором схем выбора компромиссного решения. Принимая во внимание, что вопрос о выборе схемы компромисса в условиях отсутствия полной и строгой теории принятия управленческих решений в настоящее время решается на неформальном, концептуальном уровне, рассмотрим основные наиболее часто используемые в практических расчетах схемы.

4. Метод последовательных уступок

1. Расположить критерии по убыванию их значимости.

2. Решить задачу по первому критерию , то есть отыскать субоптимальное* решение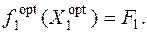

3. Сделать «уступку» по первому критерию, т. е. уменьшить величину до значения .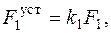

4. Ввести в модель дополнительное ограничение

.

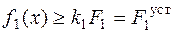5. Решить задачу по второму критерию , т. е. найти субоптимальное решение **= F ₂.

6. Сделать уступку по второму критерию

.

7. Ввести в задачу дополнительное ограничение

.

8. Решить задачу по третьему критерию

и т. д.

Субоптимальный план, найденный при решении последней задачи, является оптимальным компромиссным планом в данной схеме компромисса.

Ниже на рис. 4.1. приводится наглядная графическая иллюстрация данного метода для случая трех целевых функций. Метод последовательных уступок, являясь чрезвычайно простым и понятным в реализации, обладает, тем не менее, целым рядом недостатков, основными из которых яв­ляются:

1. Сложность и субъективизм в ранжировании критериев.

2. Субъективизм в задании величин уступок.

3. Степени достижения оптимума (безусловного) по всем критериям, кроме первого, неопределены. Рассчитать их можно, лишь решив исходные модели по соответствующим целевым функциям (еще задач) на глобальный оптимум.

4. Поскольку уступка по последнему критерию не делается, степень достижения оптимума по нему может оказаться совершенно неудовлетворительной. Для «исправления» плана в этом случае все расчеты должны быть повторены с другими (причем не гарантирующими нужных окончательных результатов) коэффициентами уступок.

5. Метод минимизации суммы относительных степеней
достижения цели*

Общий вид модели, формализующей данную схему компромисса, будет следующим:

при ,

где 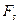– лучшее, оптимальное значение целевой функции ();

– текущее значение целевой функции ().

Основным недостатком данной схемы является взаимокомпенсация влияния локальных целевых функций (показателей) на целевую функцию глобальной модели.

Для устранения данного недостатка в модель должны быть добавлены дополнительные ограничения, «следящие» за тем, чтобы по определенному набору локальных целевых показателей не были получены их недопустимые минимальные уровни.

6.Метод минимизации равных относительных степеней достижения цели

Если под компромиссным решением понимать такой план, который по каждому целевому показателю обеспечивает одинаковые относительные отклонения от оптимальных решений, то соответствующая математическая модель, позволяющая найти это решение, будет иметь вид

при .

Читателю предлагается самостоятельно привести модель к линейному виду, считая, что целевые функции и функции затрат всех ресурсов линейны.

Недостатки метода:

1. Уравнительный характер искомого компромиссного плана.

2. Наихудший (по степени достижения цели) показатель определяет результаты по всем остальным компонентам целевой вектор-функции.

7. Метод максимизации минимальной относительной степени достижения цели

Свободным от недостатков рассмотренных выше методов является метод, в котором компромисс формализуется как поиск решения, максимизирующего по всем показателям относительную минимальную степень достижения цели.

Рассмотрим эту схему компромисса более подробно.

I этап. Все критерии делаются «однонаправленными», например, решаемыми на максимум. Достигается это изменением знака на обратный в целевых функциях, соответствующих минимизируемым показателям.

Получаем модель

при .

II этап. Исходная модель решается по каждой целевой функции в отдельности, а результаты решения сводятся в таблицу следующего вида:

Целевые функции	Оптимальные планы	Целевые функции
f 1(x)	f 2(x)	…	f s(x)
f 1(x)				…
f 2(x)				…
…	…	…	…	…	…
fs (x)				…
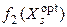
Fs – max по столбцу	F 1	F 2	…	Fs
fs – min по столбцу	f 1	f 2	…	fs
D s = Fs – fs	D1	D2	…	D s

 

III этап. При решении одноцелевых задач «автоматически» отыскивается наибольшая степень достижения цели. В случае же многоцелевой оптимизации, как уже отмечалось, степень достижения абсолютного оптимума не может быть наибольшей по всем критериям сразу, а, следовательно, возникает проблема ее измерения. В абсолютном измерении степень достижения цели по показателю может быть рассчитана по формуле , т. е. как степень удаления текущего значения функ­ции от наименьшего ее значе­ния (от найденных субоптимальных планов). Графически это выгля