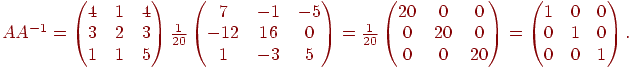Элементарными преобразованиями матриц являются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Определение. Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований.
Записывается А ~ В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю.
Такую матрицу называют канонической, например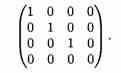 
УМНОЖЕНИЕ НА ЧИСЛО
Определение 10. Произведением матрицы A=(aij) на число k называется такая матрица C=(cij), элементы которой сij равны элементам матрицы A, умноженным на число k, т.е.у которой(cij) = (kaij).
Для операции произведение матрицы на число справедливы следующие соотношения:
· kA=Ak;
· k(A+B)=Ak+Bk;
· (k+λ)A=Ak+Aλ;
· k(λA)=λkA=λ(kA).
Определение 11. Матрица B, у которой все элементы равны элементам матрицы A по абсолютной величине, но имеют противоположные знаки по сравнению со знаками соответствующих элементов матрицы A, называется противоположной матрице A и записываетсяA=(-1)(aij).
Заметим, что умножение любой матрицы на нулевую дает в результате нулевую матрицу, как и в обычной алгебре, т.е. 
·A= .
Если A - квадратная матрица, то тогда очевидно равенство det(λA)=λndetA, где n - размер матрицы A.
Пример.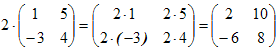 
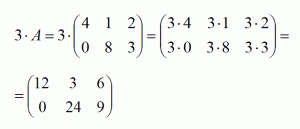
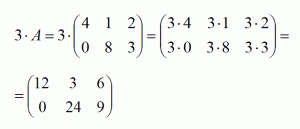
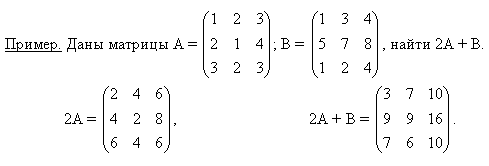
ПРОИЗВЕДЕНИЕ
Определение 12. Если A=(aij)m×p, а B=(bij)p×n, то произведением матрицы A на матрицу B назовем матрицу C, каждый элемент которой вычисляют по формуле:
|
|
Из определения 12 видно, что каждый элемент матрицы C = AB, расположенный в s-ой строке и k-ом столбце равен сумме произведений элементов s-ой строки матрицы A на элементы k-го столбца матрицы B.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.
Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.
Можно представить все это в виде схемы: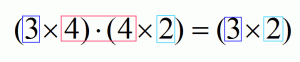 
После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.
Посмотрим как это выглядит на схеме: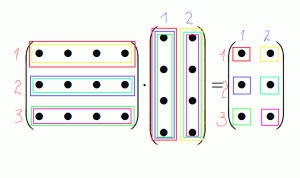 
При перемножении матриц можно воспользоваться следующей таблицей. Покажем этот на примере.
|
|
Пусть требуется перемножить матрицы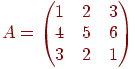 
и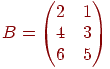 
, т.е. найти AB Составим таблицу: слева запишем элементы матрицы А (которую умножают), а снизу – элементы матрицы В (на которую умножают):
Результат будем записывать в выделенных ячейках, по формуле – сумма произведений соответствующих элементов:
| 1·2+2·4+3·6 | 1·1+2·3+3·5 | |||
| 4·2+5·4+6·6 | 4·1+5·3+6·5 | |||
| 3·2+2·4+1·6 | 3·1+2·3+1·5 | |||
Произведя вычисления, получаем:
Это и будет искомая матрица (в выделенных ячейках):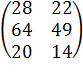 
Пример.
Найти произведение матриц А и В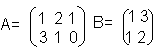 
Произведение А∙В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2).
При этом определено произведение В∙А, которое считают следующим образом:
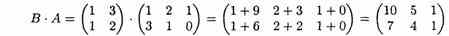
Пример.
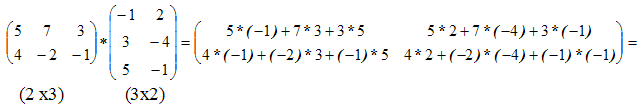
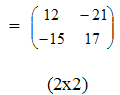
Пример.
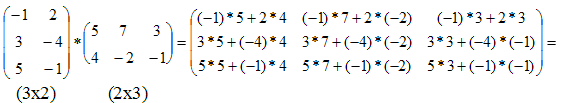
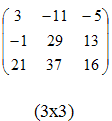
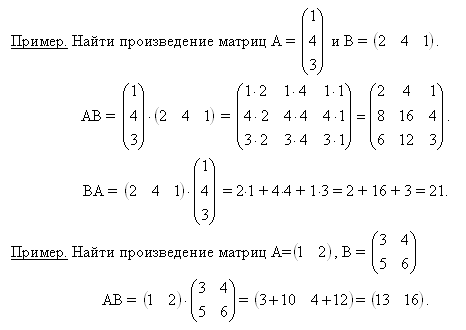
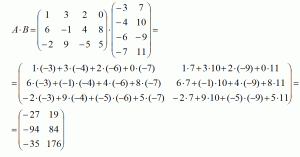
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют.
Определение 13. Если AB = BA, то такие матрицы A и B называют перестановочными или коммутативными.
Очевидно, что коммутативной с единичной будет любая матрица подходящего размера AE = EA = A.
Известны следующие очевидные свойства произведений матриц:
|
|
Теорема. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц, т.е. det(AB) = detA·detB.
ТРАНСПОНИРОВАНИЕ
Определение 14. Если в некоторой матрице A поменять местами столбцы и строки, то полученная матрица будет называться транспонированной и обозначается Aт.
Определение 15. Если выполняется равенство A = Aт, то такая матрица называется симметрической.
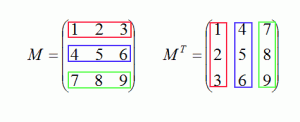
Например, дана матрица М, каждую строчку этой матрицы перенесем в соответствующий столбец матрицы, стоящей на рисунке рядом. Вторая матрица - это транспонированная матрица матрицы М.
Пример. 
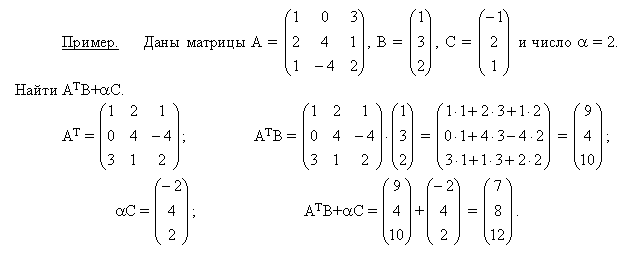
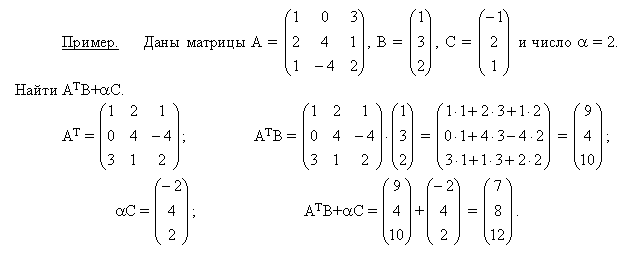
ДЕЛЕНИЕ
Деление матриц - понятие которое не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней. Согласно этому свойству разделим матрицу А на матрицу В:
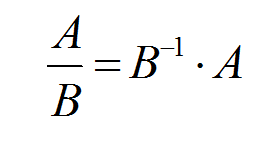
В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.
Определение 16. Обратной по отношению к матрице A называется такая матрица, для которой выполняется равенство AA-1 = A-1A = E.
Определение 17. Матрица, которая имеет обратную называется обратимой или не особенной.
Теорема. Для того, чтобы матрица A имела обратную матрицу A-1 необходимо и достаточно, чтобы она была бы невырожденной, т.е. detA 
0.
Алгоритм вычисления обратной матрицы:
Покажем это на примере квадратной матрицы третьего порядка.
Пусть дана матрица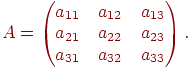 
1. Вычислить detA 0;
2. Вычислить все алгебраические дополнения матрицы A;
Их количество всегда равно числу элементов матрицы. Если матрица третьего порядка, значит у нее 9 элементов, у каждого свое дополнение и все эти дополнения надо искать.
Ais = (-1)i+s Mis.
3. Составим присоединенную матрицу из полученных алгебраических дополнений, которая обычно обозначается как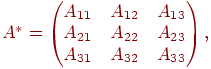 
4. Транспонируем её.
5. После нахождения всех дополнений составляем обратную матрицу.
Пример. Пусть дана матрица В: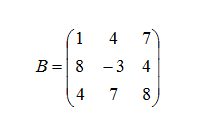 
Найдем ее определитель:
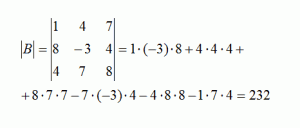
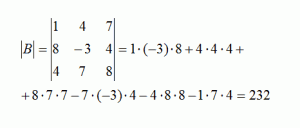
Определитель равен 232, это не ноль, значит матрица невырожденная и для нее можно найти обратную матрицу. Для этого найдем 9 дополнений:
Дополнение для элемента, стоящего в первой строке первого столбца:
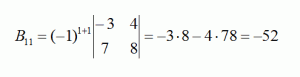
Дополнение для элемента, стоящего в первой строке второго столбца:
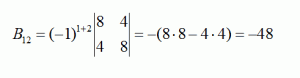
Дополнение для элемента, стоящего в первой строке третьего столбца:
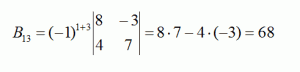
Теперь определим следующие три дополнения для второй строки:
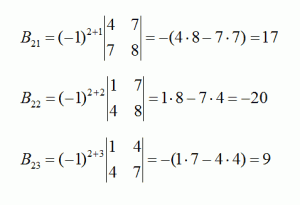
И последние три для третьей строки:
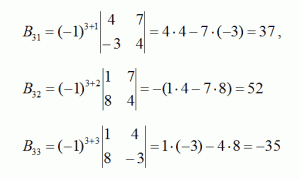
Теперь составим обратную матрицу:
Пример.
Найти обратную матрицу для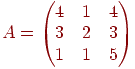 
и выполнить проверку.
Решение. Вычисляем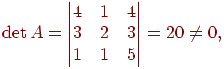 
следовательно, обратная матрица существует. Найдем присоединенную матрицу A*. Для этого вычислим все миноры второго порядка матрицы A и алгебраические дополнения:
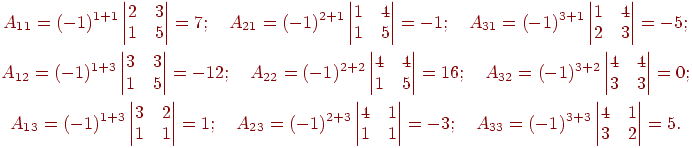
Составим (А*)Т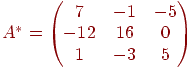 
и найдем по формуле обратную матрицу:
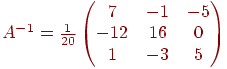
Проверка 