Таким образом при заданных условиях обстановки для компании «ПЕГМЕНТ» оптимальным выбором будет ежедневное производство 2.4 тонны краски для наружных работ и 1.4 тонн краски для внутренних работ с ежедневным доходом 12 800$.
Вполне реально предположить, что полученное статистическое решение может устареть еще до момента его реализации. Поэтому следует предусмотреть динамический характер условий производства и продажи красок. Так, например, важно знать, как повлияет на оптимальное решение увеличение или уменьшение спроса, изменение рыночных цен или запасов исходного сырья. Следовательно, необходимо провести анализ модели на чувствительность, позволяющий определить зоны устойчивого функционирования предприятия на рынке товаров.
В нашем примере связывающими ограничениями являются ограничения представленные прямыми (1) и (3). Ограничение (1) определяет запасы сырья А (см. табл. № 1). Ограничение (3) определяет соотношение спроса на выпускаемую продукцию (краску для наружных работ). Т.е. сырье А и соотношение спроса на выпускаемую продукцию (краску для наружных работ) является дефицитными ресурсами.
Не связывающими ограничениями являются ограничения представленные прямыми (2) и (4). Ограничение (2) определяет запасы сырья В (см. табл. 1). Ограничение (4) определяет соотношение спроса на выпускаемую продукцию (краски для внутренних работ). Следовательно ресурсы, сырье В и спрос на выпускаемую продукцию (краску для внутренних работ) являются не дефицитным ресурсами.
Рассмотрим сначала ресурс – сырье А. При увеличении запаса этого ресурса прямая (1) перемешается в верх, параллельно самой себе, до т. К, в которой пересекаются прямые соответствующие ограничениям (2), (3), (4). Тогда в данной точке эти ограничения становятся связывающими и в этом случае координаты т. К соответствуют оптимальному решению. Но тогда в этой точке ограничение (1) становится избыточным, т.к. любой дальнейший рост запасов сырья А не влияет ни на область допустимых решений, ни на оптимальное решение. Этот предельный уровень запаса сырья А находиться следующим образом:
- определяются координаты т. К ( 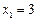 ,
,  );
);
- находиться решение системы уравнений (2), (3), (4):
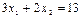
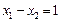
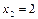
В результате определяется максимально допустимый запас сырья А = 12 т. При этом получим приращение дохода на выпускаемую продукцию:
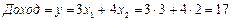
Проиллюстрируем ситуацию, когда рассматривается вопрос об изменении соотношения спроса на выпускаемую продукцию, определяемую ограничением (3). При увеличении соотношения спроса на выпускаемую продукцию прямая (3) перемещается вниз параллельно самой себе, до т. Е, в которой пересекаются прямые соответствующие ограничениям (1), (2). Координаты данной т. Е можно найти графически или решением системы уравнений (1) и (2):

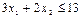
В результате получается  ,
,  . При этом ежедневный спрос на краску для наружных работ не буде превышать спрос на краску для внутренних работ на величину 4.2 – 0.2 = 4 т. При этом получим приращение дохода на выпускаемую продукцию:
. При этом ежедневный спрос на краску для наружных работ не буде превышать спрос на краску для внутренних работ на величину 4.2 – 0.2 = 4 т. При этом получим приращение дохода на выпускаемую продукцию:
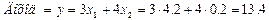
Дальнейшее увеличение разрыва в спросе на выпускаемую продукцию не будет влиять на оптимальное решение.
Рассмотрим вопрос об уменьшении избыточного сырья В. Ограничение (4) фиксирует предельный уровень спроса на краску для внутренних работ. Из рис. 1 следует, что, не изменяя оптимального решения, прямую (4) можно опустить вниз до пересечения с оптимальной т. С. Т.к. т. С имеет координаты 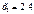 ,
, 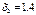 , уменьшение спроса на краску для внутренних работ до величины
, уменьшение спроса на краску для внутренних работ до величины  не повлияет на оптимальность ранее полученного решения. Рассмотрим теперь ограничение (2), которое представляет собой ограничение на недефицитный ресурс-сырье В. И в этом случае запасы сырья В можно уменьшать до тех пор, пока прямая (2) не достигнет т. С. При этом правая часть ограничения (2) станет равной:
не повлияет на оптимальность ранее полученного решения. Рассмотрим теперь ограничение (2), которое представляет собой ограничение на недефицитный ресурс-сырье В. И в этом случае запасы сырья В можно уменьшать до тех пор, пока прямая (2) не достигнет т. С. При этом правая часть ограничения (2) станет равной:
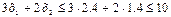
Этот результат показывает, что ранее полученное оптимальное решение не измениться, ели ежедневный запас сырья В уменьшиться на 3 т. Результаты произведенного анализа заносятся в таблицу № 2.
Таблицу № 2 – Результаты анализа
| Ресурс | Вид ресурса | Тип ресурса | Максимальное изменение запаса ресурса (Dр) | Максимальное приращение дохода от изменения ресурса (Dу) |
| сырье А | дефицитный | 12 – 9 = 3 | 17 – 12.8 = 4.2 | |
| сырье В | не дефицитный | 10 – 13 = - 3 | 12.8 – 12.8 = 0 | |
| спрос на краску для наружных работ | дефицитный | 4 – 1 = 3 | 13.4 – 12.8 = 0.6 | |
| спрос на краску для внутренних работ | не дефицитный | 1.4 – 2 = - 0.6 | 12.8 – 12.8 = 0 |
Пример № 1 (продолжение)
Результаты произведенных расчетов представим таблицей № 3. Полученные результаты свидетельствуют о том, что дополнительные вложения в первую очередь следует направить на увеличение дефицитного ресурса 1 – сырья А и лишь затем – на формирование соотношения спроса на выпускаемую продукцию.
Таблицу № 3 – Результаты анализа
| Ресурс | Вид ресурса | Тип ресурса | Значение Z |
| сырье А | дефицитный | 
| |
| сырье В | не дефицитный | 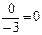
| |
| спрос на краску для наружных работ | дефицитный | 
| |
| спрос на краску для внутренних работ | не дефицитный | 
|
Пример № 1 (продолжение)
При изменении коэффициентов ЦФ с1, с2 т. С остается точкой оптимального решения до тех пор, пока угол наклона у будет лежать между углами наклона двух прямых (1) и(3), пересечением которых является т. С. Этим прямым соответствуют ограничения (1) и (3):

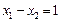
Алгебраически это можно записать следующим образом:
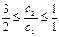 ,
, 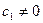
или
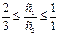 ,
, 
Если исходное значение коэффициента с2 = 4 оставить неизменным, то видно (см. рис. 2), что значение коэффициента с1 можно уменьшить до тех пор, пока прямая уmax не совпадет с прямой (1).
Это крайнее минимальное значение коэффициента с1 можно определить из равенства углов наклона прямой ЦФ и прямой (1). Так как тангенс угла наклона прямой ЦФ равен  , а для прямой (1) равен
, а для прямой (1) равен  , то минимальное значение коэффициента с1 определим из равенства:
, то минимальное значение коэффициента с1 определим из равенства:
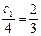
откуда коэффициент 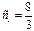 . Из рис. 2 видно, что значение коэффициента с1 можно увеличивать беспредельно, т.к. прямая у при с2 = 4 и с1 = µ не совпадет с прямой (3).
. Из рис. 2 видно, что значение коэффициента с1 можно увеличивать беспредельно, т.к. прямая у при с2 = 4 и с1 = µ не совпадет с прямой (3).
Следовательно, при всех значениях коэффициента 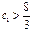 т. С будет единственной точкой, в которой решение будет оптимальным, и это не снимет проблему дефицита ресурсов 1 и 3.
т. С будет единственной точкой, в которой решение будет оптимальным, и это не снимет проблему дефицита ресурсов 1 и 3.
При 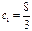 оптимальными угловыми точками будут как т. С, так и т. В. Как только значение коэффициента
оптимальными угловыми точками будут как т. С, так и т. В. Как только значение коэффициента 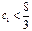 , оптимум сместится в т. В. В этом случае ресурс 3 становиться недефицитным, а ресурс 4 – дефицитным.
, оптимум сместится в т. В. В этом случае ресурс 3 становиться недефицитным, а ресурс 4 – дефицитным.
Для фирмы это означает следующее: если доход от продажи единицы продукции краски для наружных работ станет меньше  , то наиболее выгодная производственная программа предприятия должна предусмотреть выпуск максимально допустимого количества продукции – краски для внутренних работ, т.е. полностью удовлетворять спрос на данную продукцию. При этом соотношения спроса на выпускаемую продукцию не будет лимитировать объемы производства, что обусловит недефицитность ресурса 3.
, то наиболее выгодная производственная программа предприятия должна предусмотреть выпуск максимально допустимого количества продукции – краски для внутренних работ, т.е. полностью удовлетворять спрос на данную продукцию. При этом соотношения спроса на выпускаемую продукцию не будет лимитировать объемы производства, что обусловит недефицитность ресурса 3.