Экономико-математическая постановка задачи
Компания «ПЕГМЕНТ» производит краску для внутренних и наружных работ из сырья двух типов А и В, которая поступает в оптовую продажу. Нормативный расход сырья для производства краски и получаемый доход от ее продажи представлен в таблице № 1.
Таблица № 1 – Исходные данные
| Расход сырья на тонну краски (т) | Максимально возможный ежедневный расход сырья (т) | |||
| для наружных работ | для внутренних работ | |||
| Сырье | А | |||
| В | ||||
| Оптовые цены ед. продукции за тонну (в $ 1000) |
Из-за отсутствия надлежащего спроса отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т. и поставил условие, чтобы ежедневное производство краски для наружных работ не превышало более чем на тонну аналогичный показатель краски для внутренних работ. Максимально-возможный ежедневный расход сырья определяется его возрастающим спросом и возможностями складского хранения.
Встает проблема в производстве количества каждого вида продукции, чтобы доход от реализации продукции был максимальным.
Уяснение оперативно тактической постановки задачи
· Цель действий: Получение максимального ежедневного дохода от продажи, выпускаемой продукции.
· Цель математического моделирования: обоснование оптимального соотношения объема выпускаемой продукции при заданных условиях.
· Показатель эффективности определим из цели действия – ежедневный доход от продажи, выпускаемой продукции.
· Данный случайный процесс представим в виде экономической системы в структурной форме (см. рис.1):
Элементами системы являются:
- сырье;
- ежедневный объем производства различных видов краски;
- ежедневный доход от продажи, выпускаемой продукции;
- условия среды.
Среда взаимодействия с экономическая системой компании накладывает определенные условия, которым должен удовлетворять ежедневный объем производства различных видов краски. Эти условия должны учитывать ограниченные возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию.

Рисунок 1
Графический метод
Разработка математической модели
По условию задачи нам неизвестен ежедневный объем производства различных видов краски. Обозначим эти объемы как неизвестные переменные модели:
х1 – ежедневный объем производства краски для наружных работ;
х2 - ежедневный объем производства краски для внутренних работ.
Доход, получаемый от продажи ежедневного объема производства каждого вида выпускаемой продукции, является условной стоимостью, представляющий выходной величиной экономической системы. Обозначим его как сj. По условию задачи с1 = 3, с2 = 4. Тогда ежедневный доход от продажи, выпускаемой продукции можно представить в виде целевой функции:

Технологические данные производства выпускаемой продукции (в конкретном случае ежедневный расход сырья) являются заданными постоянными входными величинами. Обозначим эти величины как аij. По условию задачи а11 = 2, а12 = 3, а21 = 3, а22 = 2. Ограниченные возможности ежедневного объема производства обозначим как bi. По условию задачи ежедневный расход сырья А и В ограничен и соответственно составляет b1 = 9, b2 = 13. Тогда получаем следующие ограничения на потребление сырья:

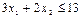
Кроме того, ограниченность спроса на готовую продукцию обязывает, чтобы максимальный ежедневный объем производства краски для внутренних работ не превышал b3 = 2, а ежедневный объем производства краски для наружных работ не превышал не более чем на тонну аналогичный показатель краски для внутренних работ b4 = 1. Тогда получаем следующие ограничения на производство выпускаемой продукции, определяющиеся спросом:


И еще одно неявное ограничение состоит в том, что переменные х1 и х2 должны быть неотрицательными.
Так как ЦФ и УО записаны в линейной форме, то данную задачу можно решить методом линейного программирования. Постановка ЗЛП осуществляется следующим образом:
Найти неотрицательные значения неизвестных переменных х1 , х2 обращающих ЦФ в максимум:
 , при
, при 
удовлетворяющих системе линейных ограничений:
неравенств, задающих условия решения задачи, определяемые ежедневным расходом сырья
 (1)
(1)
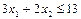 (2)
(2)
и неравенств, задающих условия решения задачи, определяемые спросом на готовую продукцию
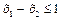 (3)
(3)
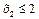 (4)
(4)
а такжеограничений на переменные
 (5)
(5)
 (6)
(6)
Данная постановка задачи имеет только единственное решение, т.к. неизвестное число переменных (n = 2) равно числу линейных ограничений системы (m = 2) как для первого, так и для второго случая.