В этом методе сортируемый массив разбивается на два отрезка: отрезок A[0],..., A[i-1] предполагается уже упорядоченным, и отрезок A[i],..., A[n-1] еще не упорядочен. Основной шаг алгоритма состоит в том, что элемент A[i] поочередно сравнивается с элементами упорядоченной части массива A[0],..., A[i-1] и вставляется в соответствующую ему позицию. Ниже приведена функция insertion, которая упорядочивает массив по возрастанию методом вставки.
Ниже приведен фрагмент процедуры сортировки, необходимый для анализа алгоритма.
for (j = 1; j < n; j++) // внеш. цикл
{ buf = A[j]; i = j-1; // с1
while (i >= 0 && A[i] > buf) // внутр. цикл
{ A[i+1] = A[i]; i--; } // с2
A[i+1] = buf; // с3
}
Время выполнения цикла while в худшем случае равно c2×j. Полное время:
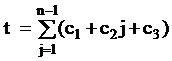 .
.
После несложных преобразований получаем:
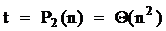 .
.
Полученная оценка относится к наихудшему случаю. В общем случае будем иметь:
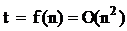 .
.
Метод слияния
Основу метода слияния составляют:
- объединение двух упорядоченных массивов в один (операция слияния);
- последовательное деление исходного массива на все более мелкие части путем использования рекурсивной процедуры с последующим их объединением.
Процедура слияния
Два упорядоченных массива (или два отрезка одного массива) объединяются в один (также упорядоченный) массив. Пусть имеем исходные массивы: А1 с числом элементов n1 и A2 с числом элементов n2. Рассмотрим процедуру слияния массивов А1 и A2 в массив A с числом элементов n = n1+n2. Предполагается, что n1 и n2 не обязательно совпадают.
На каждом шаге процедуры выполняется следующее:
- выбираем первый элемент массива А1 и первый элемент массива А2;
- меньший из них удаляем из соответствующего массива и присоединяем к имеющимся элементам результирующего массива А.
Очевидно, что для выполнения процедуры слияния таких шагов необходимо выполнить n1+n2 = n. Отсюда получаем, что время выполнения процедуры слияния будет пропорционально n (говорят, что процедура слияния является линейной по времени).
Последовательное деление
Реализуется путем использования рекурсивной процедуры, предполагающей деление заданного отрезка исходного массива на две по возможности равные части. Процесс деления завершается, если число элементов очередного отрезка равно 1. В итоге исходный массив будет представлять собой последовательность одноэлементных подмассивов.
Рассмотрим в качестве примера 8-элементный массив А = { 5, 2, 4, 6, 1, 3, 2, 6 }. Последовательное объединение подмассивов показано ниже.
Шаг 1: дробление на одноэлементные отрезки: (5), (2), (4), (6), (1), (3), (2), (6)
Шаг 2: объединение одноэл. отрезков: (2, 5), (4, 6), (1, 3), (2, 6)
Шаг 3: объединение двухэл. отрезков: (2, 4, 5, 6), (1, 2, 3, 6)
Шаг 4: последнее объединение: (1, 2, 2, 3, 4, 5, 6, 6)
Программная реализация
Ниже приведена программная реализация метода слияния для случая, когда массив упорядочивается по возрастанию.
Вспомогательная процедура слияния merge объединяет два отрезка исходного массива A с границами [p,q] и [q+1,r] и размещает результат в отрезке с границами [p,r].
void merge(int* A, int p, int q, int r)
{ int i, j, k, L= r – p + 1;
int* x = new int[L];
i = p; j = q + 1;
for (k = 0; k < L; k++) { if (j > r) { x[k] = A[i]; i++; continue; }
if (i > q) { x[k] = A[j]; j++; continue; }
if (A[i] <= A[j]) { x[k] = A[i]; i++; }
else { x[k] = A[j]; j++; }
}
for (k = 0; k < L; k++) A[p+k] = x[k];
delete[] x;
}
Главная процедура sort_merge выполняет сортировку произвольного отрезка массива A с числом элементов n и с границами [p,r].
void sort_merge(int* A, int n, int p, int r)
{ int q;
if (p < r) { q = (p + r) / 2;